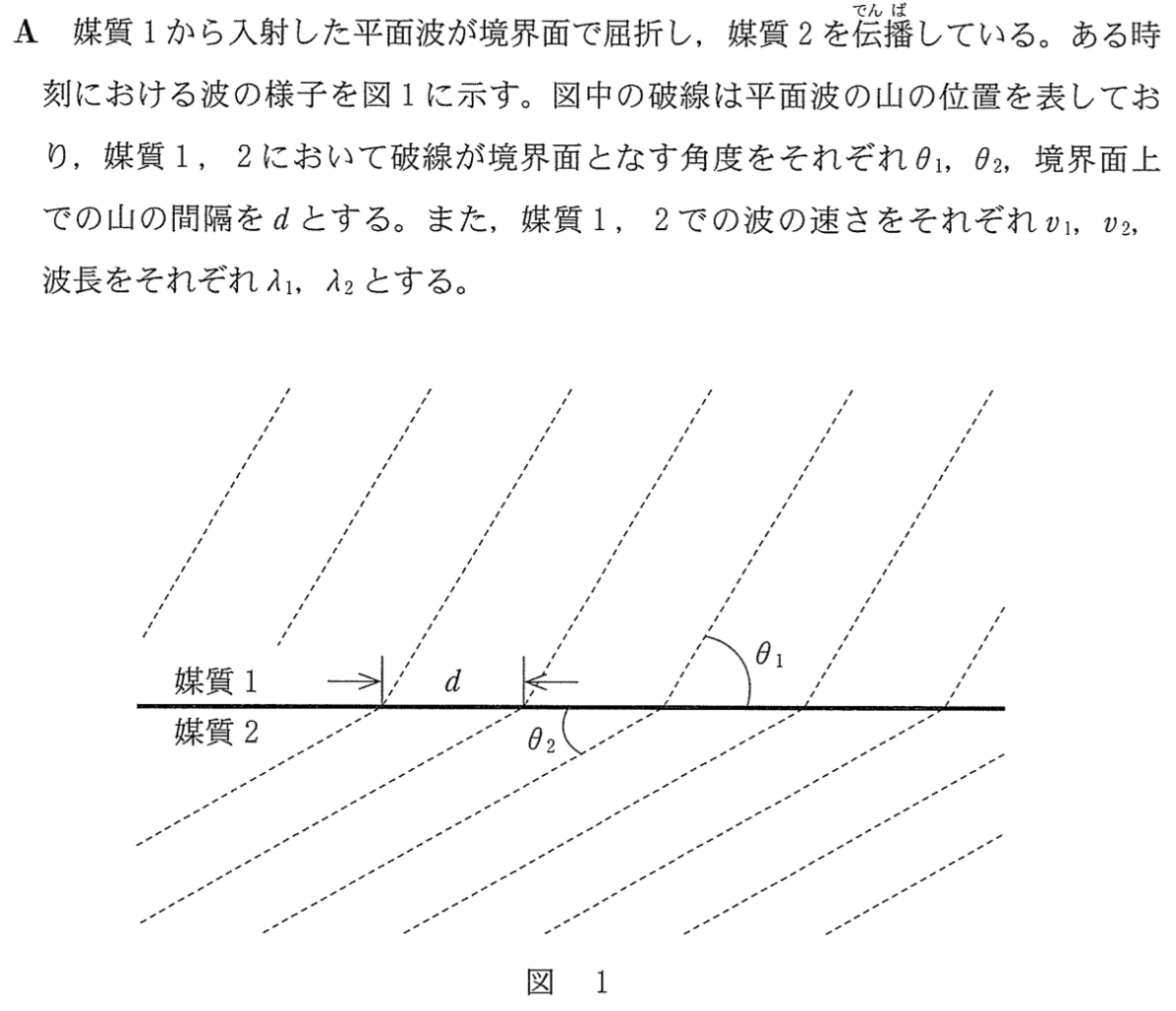

波が動いているのは、なんとなく分かるけど、問1の問題の意味が全く分からないわ。
問題の設定自体は、よく見かけるものだね。だけどちょっと確認しておこうか。
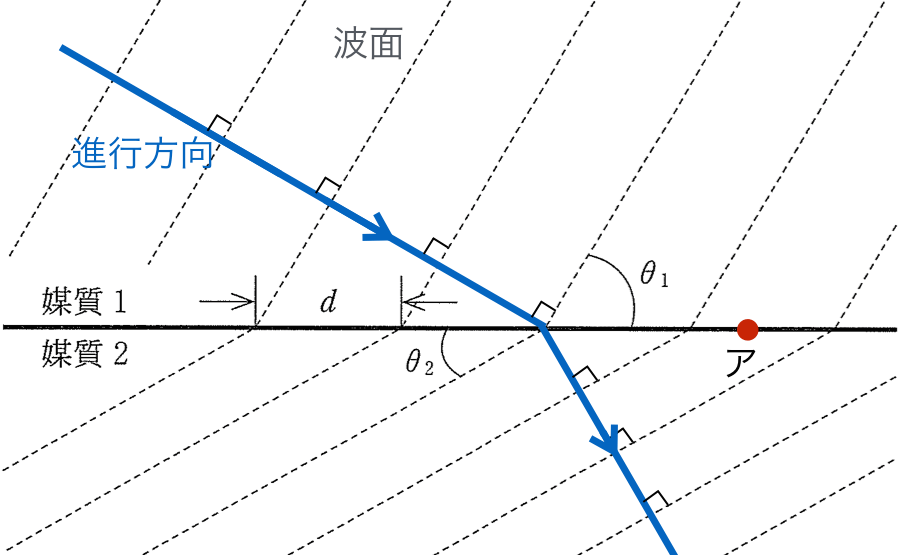
問題文では、破線は山の位置を表しているって書いてあるけど、「波面」っていうのね。
そうだね。大切なのは、青い線で示している「波の進行方向」と「波面」は垂直になるっていうことなんだ。
問題文に「境界面上の一点において」と書いてあるので、その点を赤い丸「ア」ということにしたよ。波の動きを考えると、「ア」に媒質1の山が到達して、媒質2の方へ出ていく感じがしないかな。
動きを考えるのは苦手だけど、分かる気がする。だとすると、到達する山と、出て行く山の数は絶対に同じよね。
その通り!問題文には当たり前のことが書いてあるんだよ。でもそれをヒントに式を立ててね、っていうことなんだ。
そこで、「単位時間あたりに到達する山の数」って何だろう?
う〜ん・・・。単位時間というのは、1秒と考えていいのよね。
そうだね。ということは、「1秒間に到達する山の数」っていうことだから、さらに「1秒間に到達する波の数」と考えてもいいんじゃないかな。
「山の数」と「波の数」っていうのは、確かに同じことね。
じゃあ、「1秒間に到達する波の数」って何だと思う?
正解!そうなんだよ。ちょっと回りくどい説明だけど、要は「媒質1と媒質2で振動数は同じ」っていうことを言ってるんだ。
あれ?確か屈折しても振動数は同じっていうのは、当たり前なんじゃない?
その通りだよ。これも当たり前のことが書いてあるんだ。
でもこれをヒントに式を立ててみよう。
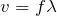
だから、媒質1と媒質2で式を立てるとどうなる?
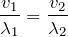
これも問題文には当たり前のことが書いてあるわね。図を見ても
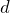
が共通なのは、明らかね。
そうだね。じゃあ、図の中で
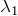
、
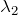
はどこか分かるかな?
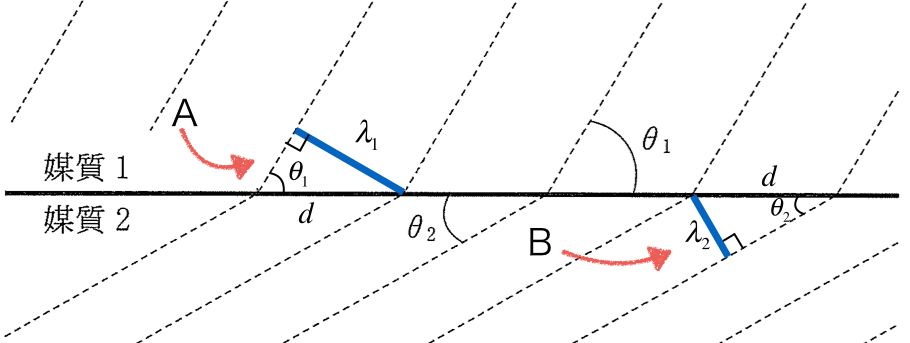
そうだね。ここで、Aと書いてある直角三角形と、Bと書いてある直角三角形で、式が立てられないかな。
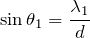
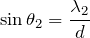
で、
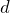
が共通なので・・・
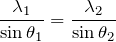

![]() だから、媒質1と媒質2で式を立てるとどうなる?
だから、媒質1と媒質2で式を立てるとどうなる?![]()
![]() 、
、![]() はどこか分かるかな?
はどこか分かるかな?![]()
![]()
![]() が共通なので・・・
が共通なので・・・![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() だから、媒質1と媒質2で式を立てるとどうなる?
だから、媒質1と媒質2で式を立てるとどうなる?![]()
![]() 、
、![]() はどこか分かるかな?
はどこか分かるかな?![]()
![]()
![]() が共通なので・・・
が共通なので・・・![]()