例えば、仕切り板を図の上に動かすと、水路の上側にある水は押され、下側にある水は引かれるよね。仕切り板を下に動かすと逆になるね。これを繰り返して、仕切り板を図の上下方向に振動されることで、水路に波を発生させているんだ。
そこで大切なのが、問題文中の「互いに逆位相の水面波が発生した」っていうところだね。設定さえ理解できれば、逆位相になりそうなことは分かるけど、そのことが明確に書かれているんだ。
なるほど。ということは、問3の文中に書かれている「仕切り板の振動の中心は、〜長さが等しくなる位置にあった。」って書いてあるから、AとBでは逆位相の波が出てくるっていうことね。
すごい!完璧だね。問3ではAとBから出てくる波が逆位相だ、ということが分かればいいんだ。そうすると、見たことのある問題じゃない?
確かに「同位相」の問題が多いけど、「逆位相」の時もあるでしょ。「同位相」が分かっていれば、「逆位相」は強め合う条件と、弱めあう条件が逆になるだけだから、そんなに難しくないよ。
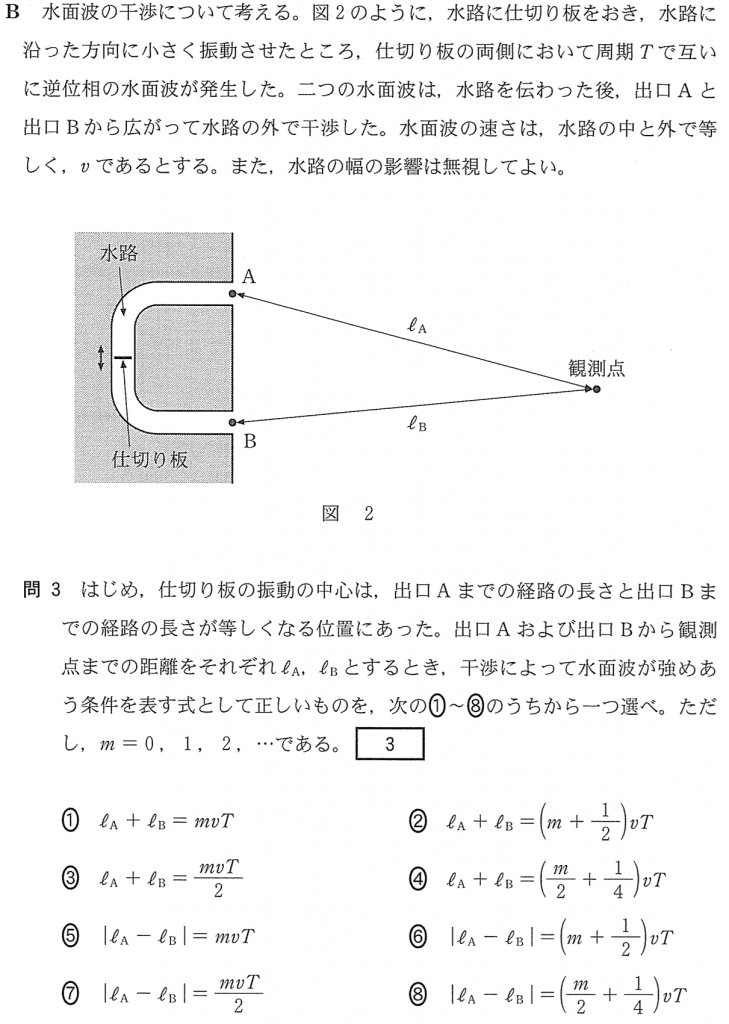
とりあえず、選択肢の中から考えると、左辺は経路差と考えて、
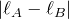
でしょ?
左辺が経路差なら、右辺は
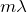
だと強め合うのよね。
いやいや、今はAとBから出る波が逆位相だから、
は弱めあう条件なんだね。
あっ、そうか。ということは、弱めあう条件はこうかな?
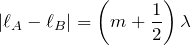
そうだね。そもそもこの問題では
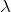
が与えられていないんだね。ということは、どうすればいい?
あと与えられているのは、波の振動の周期

と、水面波の速さ

ね。ということは、
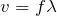
と
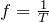
を使うと、
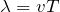
になるわね。ということは答えは⑥ね。

仕切り板をどっちに動かしたのかは分からないけど、とりあえず上に動かしたことにしてみよう。
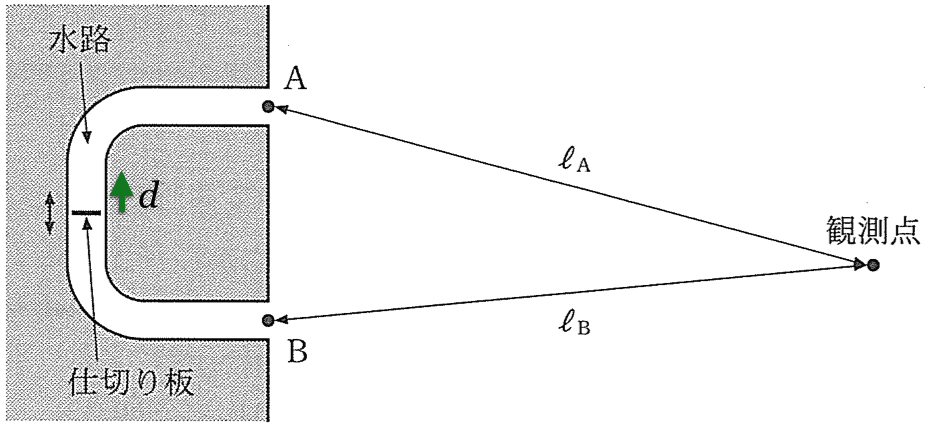
仕切り板が最初の位置にあるとして、そのときはAとBの位相が逆だったよね。
Aが山の時はBは谷、Aが谷の時はBは山、ということね。
仕切り板を振動させたときに、今、Aが山、Bが谷の時を考えてみよう。
仕切り板を上に1波長分ずらしたら、さっきと同じ瞬間にAとBはどうなっているかな。
Aは仕切り板から1波長分近づいたけど、ちょうど1波長分なら位相は変わらないわね。山は山ね。Bの方も1波長分遠くなったけど、同様に谷は谷ね。
ということは、位相は変わらないということだね。その結果、観測点でも強め合うままだね。それじゃあ、仕切り板を元に戻して、次は半波長分だけ動かした時を考えるよ。
半波長分ということは、動かす前は山だったAは谷になるわね。谷だったBは山になるわね。
そうだね。AとBはどちらも位相が逆になったけど、逆位相だっていうことは変わらないね。
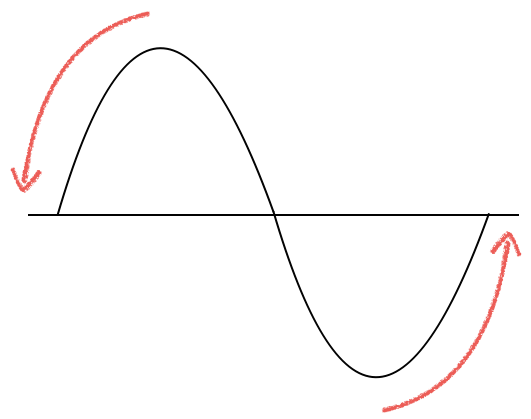
そうか。Aは山だったけど、仕切り板が近くなる分、この図だと左に移動して、Bは谷だったけど、仕切り板が遠くなる分、右に移動するっていう感じかな。
分かるわよ。ということは4分の1波長が答えね。
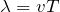
だから、
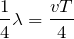
![]() は弱めあう条件なんだね。
は弱めあう条件なんだね。![]()
![]() が与えられていないんだね。ということは、どうすればいい?
が与えられていないんだね。ということは、どうすればいい?![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]() は弱めあう条件なんだね。
は弱めあう条件なんだね。![]()
![]() が与えられていないんだね。ということは、どうすればいい?
が与えられていないんだね。ということは、どうすればいい?![]()