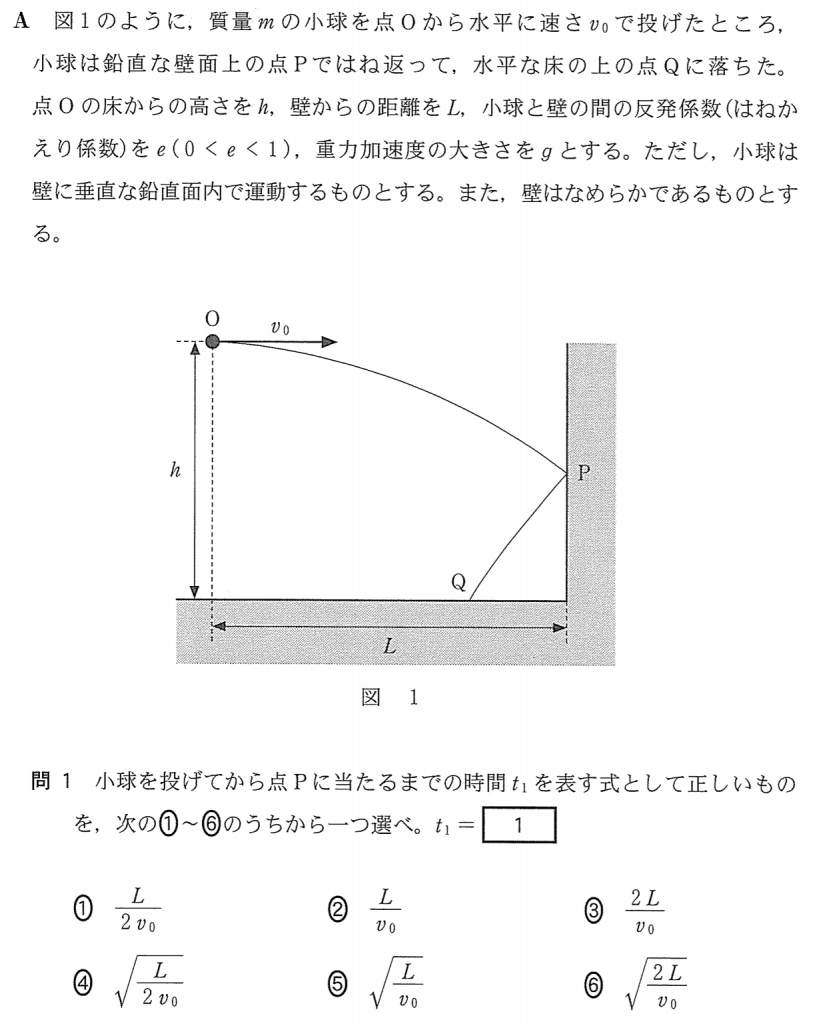
水平方向と鉛直方向を別々に考えるのよね。水平方向は等速直線運動、鉛直方向は自由落下ね。
いい感じだね。じゃあ、問1はどう考えれば良いかな?
「点Pに当たるまで」ということは、壁にぶつかるまでの話だから、水平方向だけを考えればいいわね。速さ
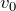
で距離
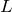
を進む時間を求めればいいから、
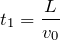
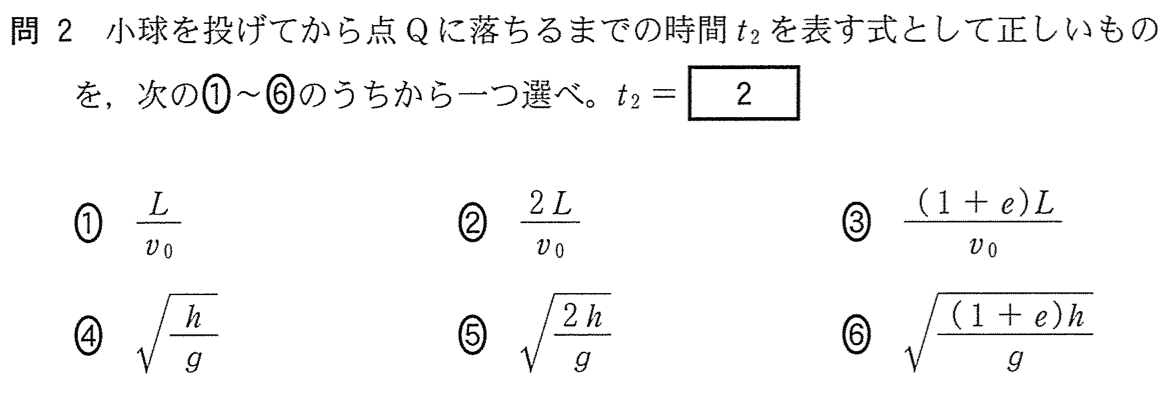
今度は「点Qに落ちるまで」、つまり床に落ちるまでの話だから、鉛直方向だけを考えれば良いわね。だけど、壁にぶつかると速さって変わらないのかな?
そうだね。速さが変わるときもあるよ。壁に平行な向き(鉛直方向)を考えると、壁と小球の間に摩擦があると遅くなるんだ。だけど今は問題文に「壁はなめらかである」と書いてあるので、摩擦は無くて速さは変わらないんだね。ちなみに壁に垂直な向き(水平方向)は、反発係数によって決まるよ。弾性衝突だと向きが変わるだけで速さは変わらないけど、今は反発係数
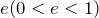
なので、遅くなるんだ。
それじゃあ壁がなめらかだから鉛直方向の速度に影響が無いとすると、単純に自由落下を考えれば良いわね。等加速度直線運動の式を使うわ。
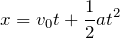
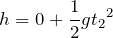
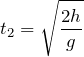

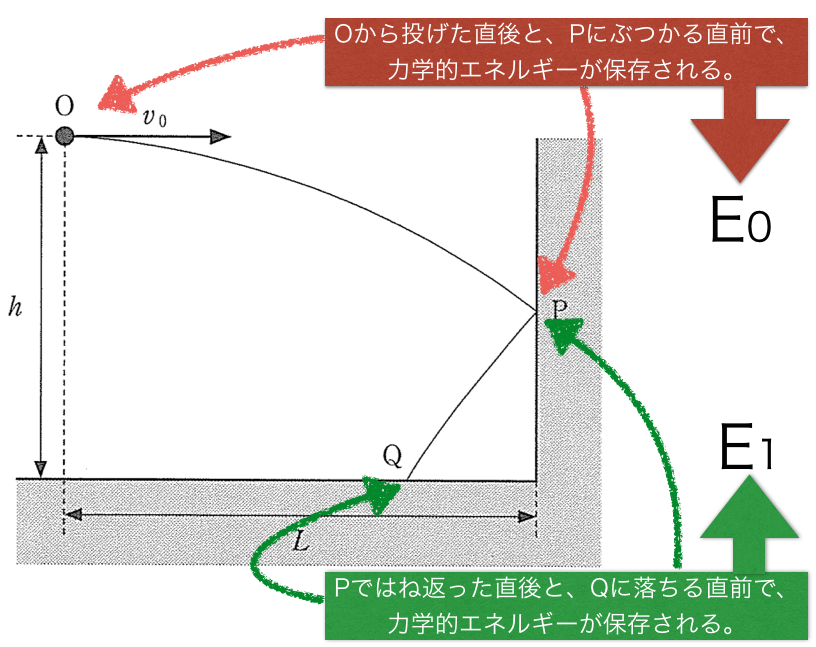
力学的エネルギーって、この場合は運動エネルギーと重力による位置エネルギーの和よね。
「力学的エネルギー保存則」っていうのがあるから、力学的エネルギーはOでもQでも等しくて、2点の差は0になるんじゃないの?
何もなければそうなんだけど、今は小球と壁との反発係数

が1より小さいので、はね返ったときに速さが遅くなるんだ。その時にエネルギーが少し減るんだよ。
なので、水平方向だけ考えるよ。水平方向のぶつかる前の速さはどうなるかな。
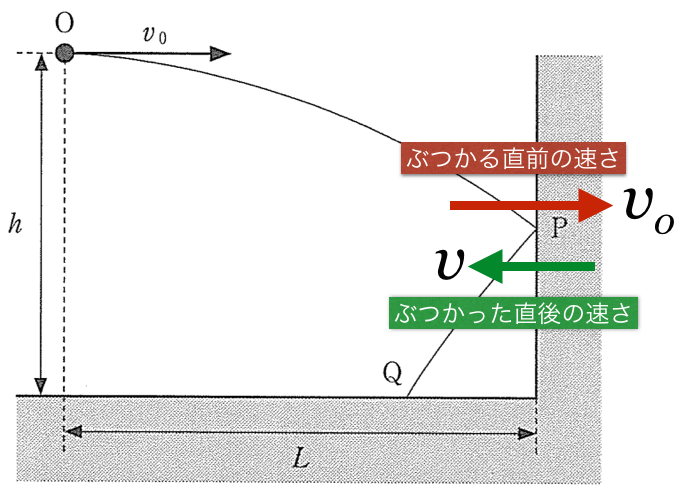
水平方向は等速直線運動なので、壁にぶつかるまではずっと
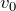
のままなのよね。
反発係数の式を使うのよね。あの式ってよく分からないの。
この「
反発係数&運動量と力学的エネルギー」のページに書いてあるとおりだね。でも反発係数は、苦手な人が多いよね。簡単に言うと、反発係数=(遠ざかる速さ)/(近づく速さ) なんだ。水平方向だけを考えれば良いので、この図を見て式が立てられるかな?
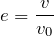
そうだね。ということは、
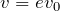
になるね。エネルギーが変化するのは、この速さの変化だけが原因なので、このエネルギーの変化分を計算すれば良いね。
運動エネルギーの変化分を計算すれば良いのね。求めたいのは

なので、
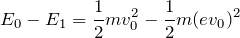
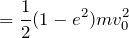
![]()
![]() なので、遅くなるんだ。
なので、遅くなるんだ。![]()
![]()
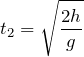
![]() が1より小さいので、はね返ったときに速さが遅くなるんだ。その時にエネルギーが少し減るんだよ。
が1より小さいので、はね返ったときに速さが遅くなるんだ。その時にエネルギーが少し減るんだよ。![]()
![]() になるね。エネルギーが変化するのは、この速さの変化だけが原因なので、このエネルギーの変化分を計算すれば良いね。
になるね。エネルギーが変化するのは、この速さの変化だけが原因なので、このエネルギーの変化分を計算すれば良いね。![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]()
![]() なので、遅くなるんだ。
なので、遅くなるんだ。![]()
![]()
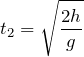
![]() が1より小さいので、はね返ったときに速さが遅くなるんだ。その時にエネルギーが少し減るんだよ。
が1より小さいので、はね返ったときに速さが遅くなるんだ。その時にエネルギーが少し減るんだよ。![]()
![]() になるね。エネルギーが変化するのは、この速さの変化だけが原因なので、このエネルギーの変化分を計算すれば良いね。
になるね。エネルギーが変化するのは、この速さの変化だけが原因なので、このエネルギーの変化分を計算すれば良いね。![]()
![]()