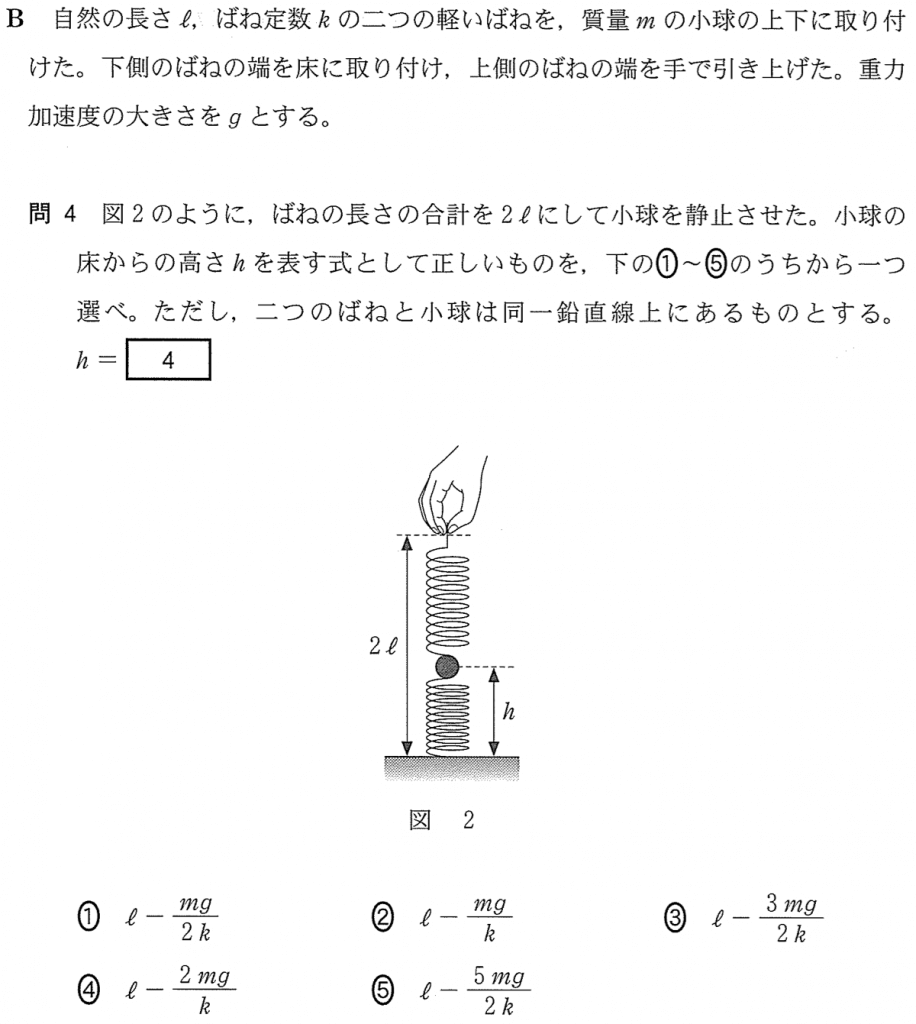
高さ
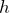
を求めるんだけど、どうすればいいと思う?
できることは限られているよね。そもそもこの小球は静止しているから、どうするかな?
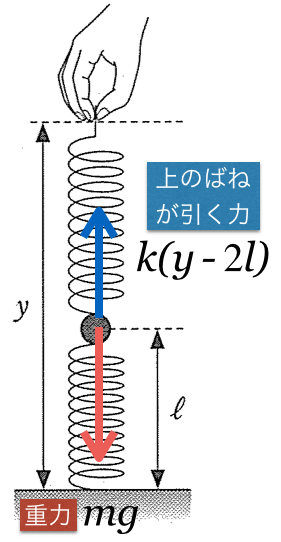
まぁ、とりあえず力の矢印を描いてみよう。小球にはどんな力がはたらいているかな?
重力と、あとはくっついているものから力を受けるのよね。くっついているのは、上のばねと下のばねの2つ。ばねから受ける力は、フックの法則
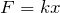
で求めることができるけど、ばねの伸びは分からないわ。
ばねは2つとも自然の長さが
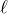
なので、図の中に描いてみると何か分かるんじゃないかな。
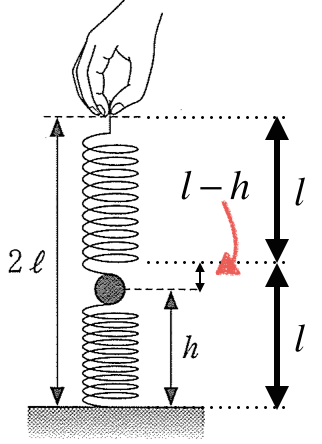
分かったわ。下のばねは
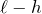
だけ縮んでいて、上のばねは
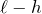
だけ伸びているんだわ。
ばねの伸び、縮みが分かったら、力の矢印を描いてみう!
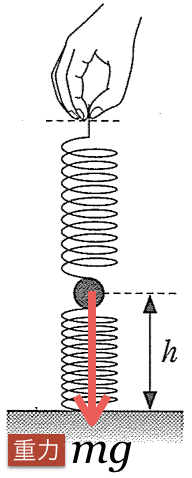
次はくっついているばねから受ける力ね。下のばねは縮んでいるから、小球を押しているのね。ということは力の矢印は上向き。ばねの伸びは
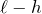
だから・・・
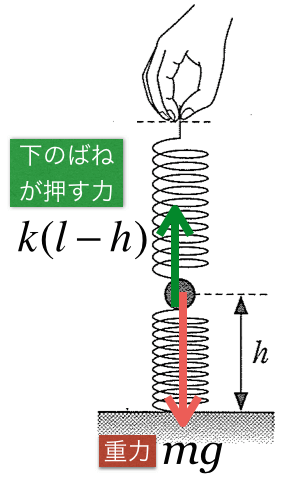
上のばねは伸びているから、小球を引いているね。ばねの伸びは
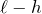
だから・・・
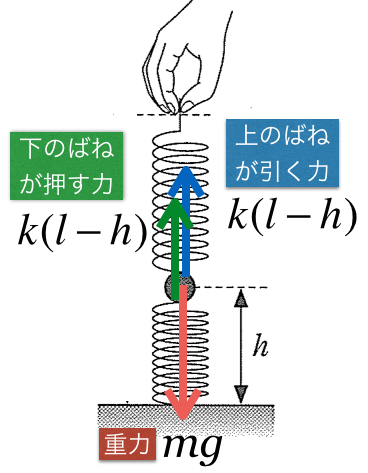
ばね以外にくっついているものはないから、これで終わりだと思うわ。
その通り!力の矢印を描き終わったら、あとはどうする?
小球は静止しているから力のつりあいの式を立てるのね。上向きを正とすると、
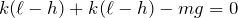
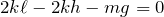
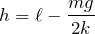
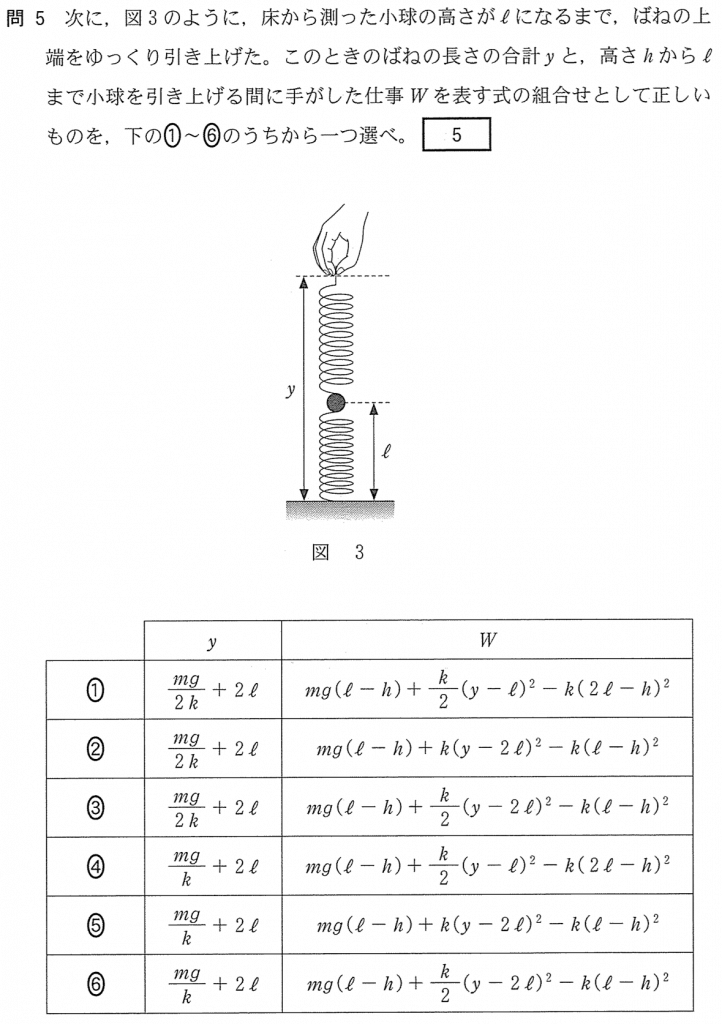
まずは
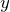
なんだけど、これもさっきと同じようにばねの伸びを求めて、力の矢印を描けばいいのかな。
ばねの自然の長さが
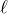
だから・・・
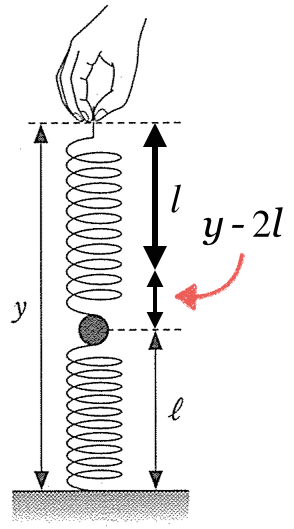
下のばねはちょうど自然の長さになっているから、小球を押したり引いたりしていないわね。上のばねの伸びは
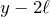
だから・・・
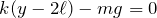
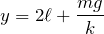
いいね、合ってるよ。ということは答えは④、⑤、⑥のどれかだね。
次はちょっと難しいわ。何をすれば良いか、分からない。選択肢を見ても長い式ばっかりだし。
そうだね。エネルギーを仕事の関係を考えると、手がした仕事
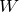
の分だけ、全体のエネルギーが増えるんだよね。この場合、考えるエネルギーは何かな?
小球は少し上に上がっているから、重力による位置エネルギーが増えているはずだわ。あとはばねの伸びが変わっているから、その分のエネルギーが変化しているわね。
それらを1つずつ考えていけば大丈夫だよ。ちょと図を描いてみるね。
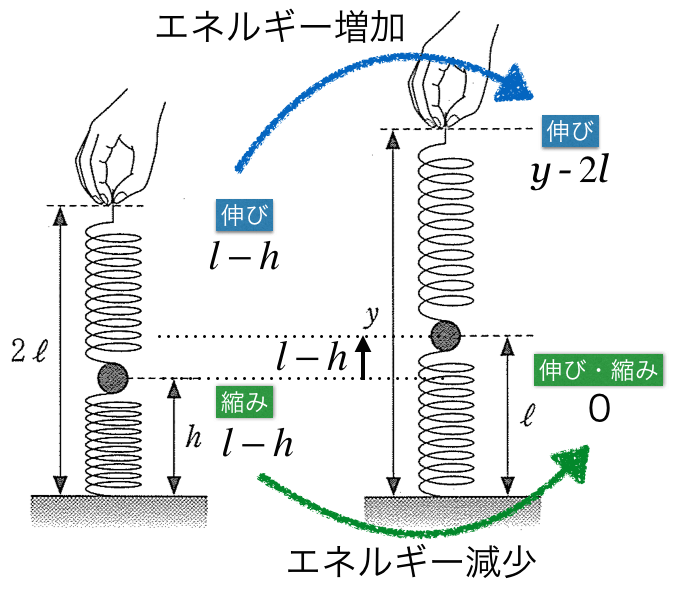
まずは重力による位置エネルギーを考えるね。
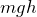
でいいわよね。図を見ると
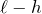
だけ上に上がっているから、重力による位置エネルギーは、
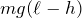
下のばねを考えてみるわ。弾性力による位置エネルギーは、
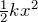
だよね。最初ばねの縮みが
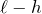
だったのが、伸び縮み0になったので、
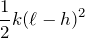
最後は上のばねね。ばねの伸びが
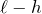
から
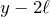
に変化したので、
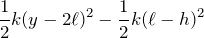
これで揃ったね。手がした仕事の分だけエネルギーが増加した、という式を立てるとどうなるかな。
下のばねだけエネルギーが減少することを忘れずに式を立てると、
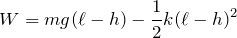
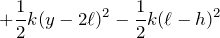
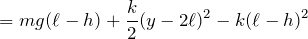
![]() を求めるんだけど、どうすればいいと思う?
を求めるんだけど、どうすればいいと思う?![]() なので、図の中に描いてみると何か分かるんじゃないかな。
なので、図の中に描いてみると何か分かるんじゃないかな。![]()
![]()
![]()
![]()
![]()
![]() の分だけ、全体のエネルギーが増えるんだよね。この場合、考えるエネルギーは何かな?
の分だけ、全体のエネルギーが増えるんだよね。この場合、考えるエネルギーは何かな?![]()
![]()
![]()
![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]() を求めるんだけど、どうすればいいと思う?
を求めるんだけど、どうすればいいと思う?![]() なので、図の中に描いてみると何か分かるんじゃないかな。
なので、図の中に描いてみると何か分かるんじゃないかな。![]()
![]()
![]()
![]()
![]()
![]() の分だけ、全体のエネルギーが増えるんだよね。この場合、考えるエネルギーは何かな?
の分だけ、全体のエネルギーが増えるんだよね。この場合、考えるエネルギーは何かな?![]()
![]()
![]()
![]()
![]()
![]()
コメント
とても分かりやすかったです!
ありがとうございます‼︎