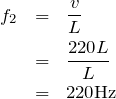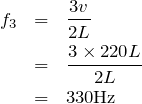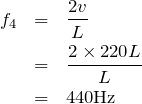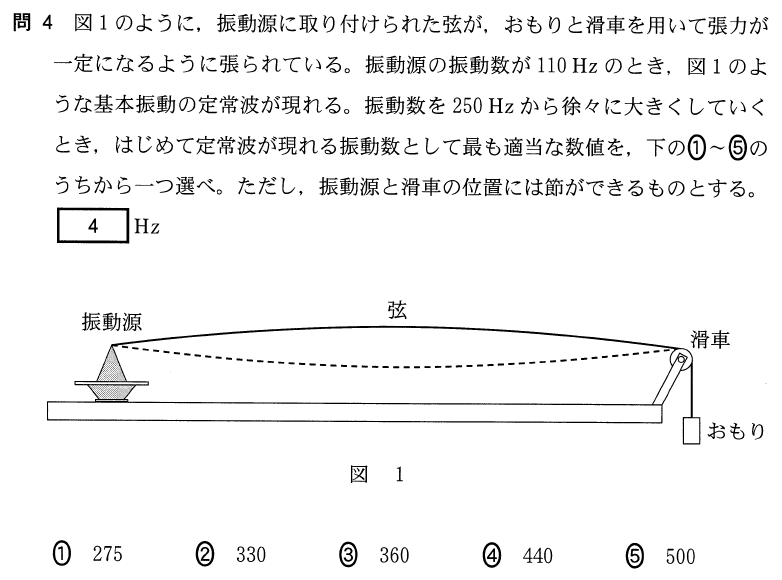
この基本振動の時の振動数が110Hzということだね。振動数を徐々に大きくしていくとどうなるか分かるかな?
徐々に大きくしていくとこのような定常波は現れなくなるけど、ちょうど良い振動数では、2倍振動、3倍振動っていう定常波が現れるのよね。
分かってるね。振動源と滑車間の長さを
とすると、こんな感じだよね。
基本振動
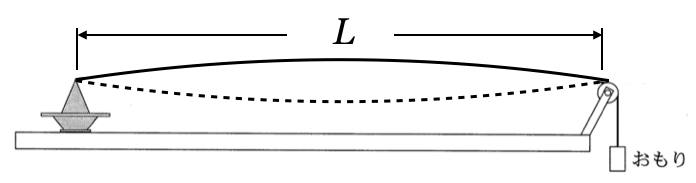
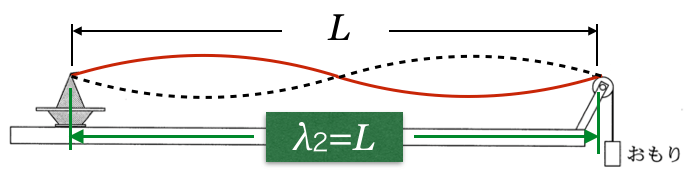
2倍振動
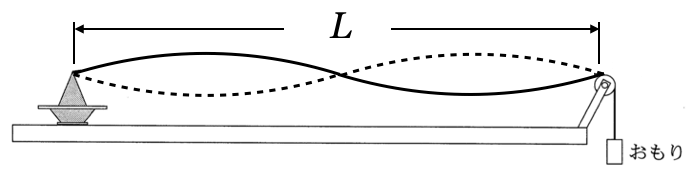
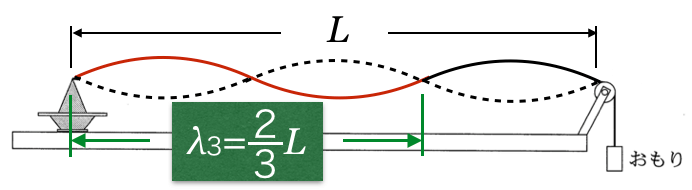
3倍振動
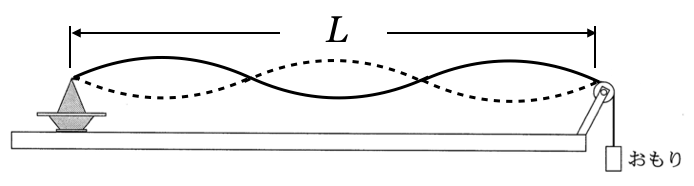
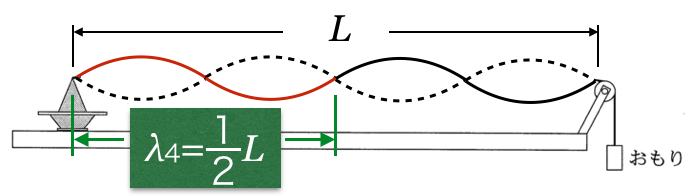
4倍振動
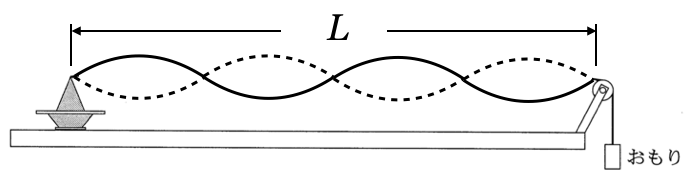
えっと、基本振動は、弦の部分を延ばして波長を考えるのよね。横に長くなっちゃうけど、こんな感じ。

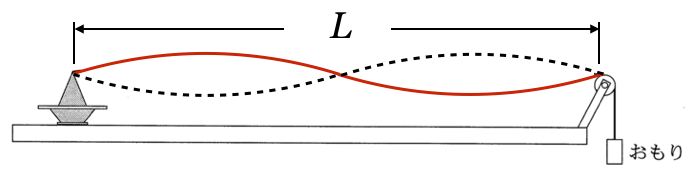
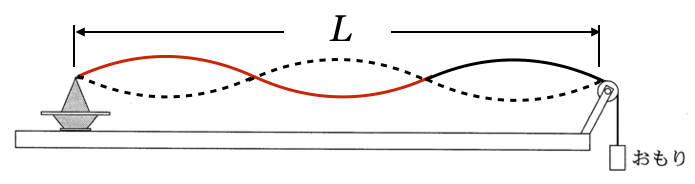
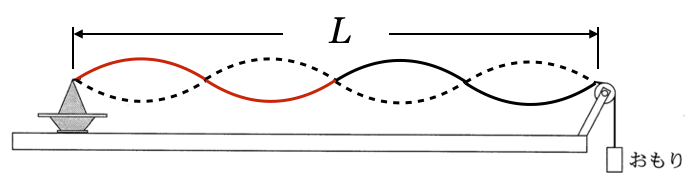
大丈夫だね。それぞれの波長を
で表してみようか。

いいね。ここまでできれば準備はできた。次はどうしよう?
できれば波の分野でよく使う
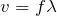
に入れたいんだけど、

が分からないのよね。
それじゃあ、

と置いちゃえばいいんじゃない?
そういうことか。じゃあ全部の図に当てはめてみるわよ。
一応、問題文に「張力が一定になるように」と書かれているので、弦を伝わる波の速さも一定なんだよね。
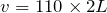
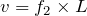
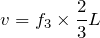
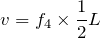
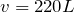
だから、他の式に代入すると、それぞれの振動数が求められるね。
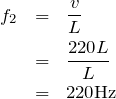
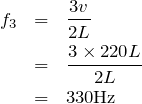
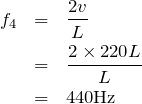
この結果で分かるのは、基本振動が110Hz、2倍振動が220Hz、3倍振動が330Hz、4倍振動が440Hzでそれぞれ定常波が現れるっていうことよね。
問題文には「250Hzから徐々に大きくしていく」って書いてあるので、250Hz以上で初めて定常波が現れるのは3倍振動の330Hzよね。

![]() とすると、こんな感じだよね。
とすると、こんな感じだよね。







![]() で表してみようか。
で表してみようか。



![]() に入れたいんだけど、
に入れたいんだけど、![]() が分からないのよね。
が分からないのよね。![]() と置いちゃえばいいんじゃない?
と置いちゃえばいいんじゃない?![]()
![]()
![]()
![]()
![]()
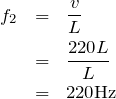
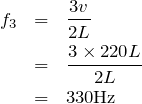
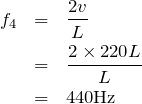
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() とすると、こんな感じだよね。
とすると、こんな感じだよね。







![]() で表してみようか。
で表してみようか。



![]() に入れたいんだけど、
に入れたいんだけど、![]() が分からないのよね。
が分からないのよね。![]() と置いちゃえばいいんじゃない?
と置いちゃえばいいんじゃない?![]()
![]()
![]()
![]()
![]()