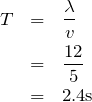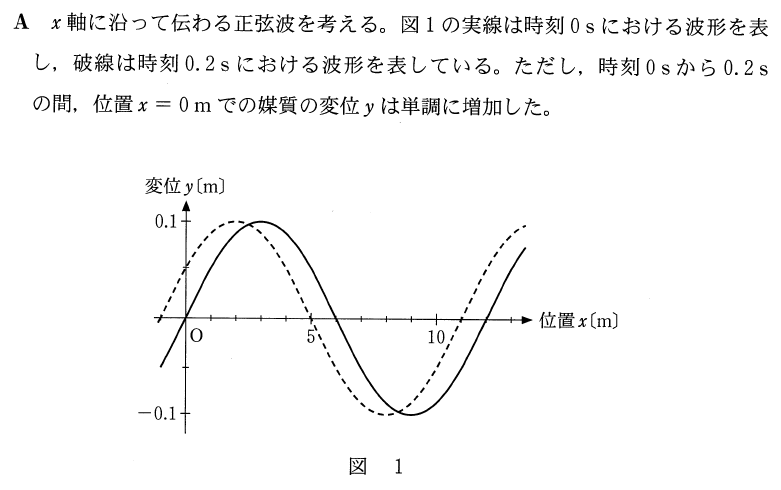

波のグラフは横軸が

か

かを確認することが大切なのよね。
そうだね。この問題では横軸が

だね。横軸が

のグラフからは何が分かるんだっけ?
横軸が

のグラフは、ある時刻の波形を表しているんだから、波長が分かるのね。
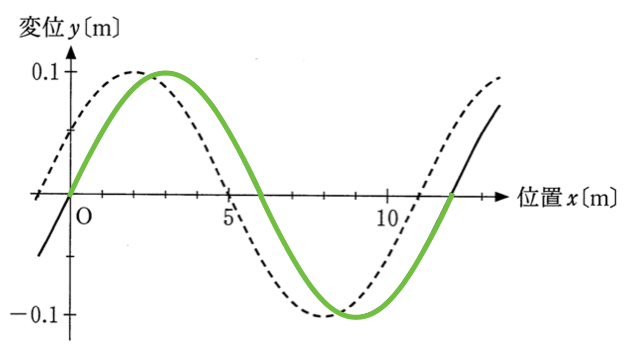
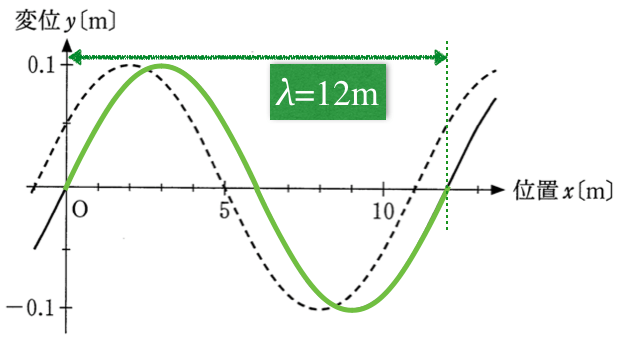
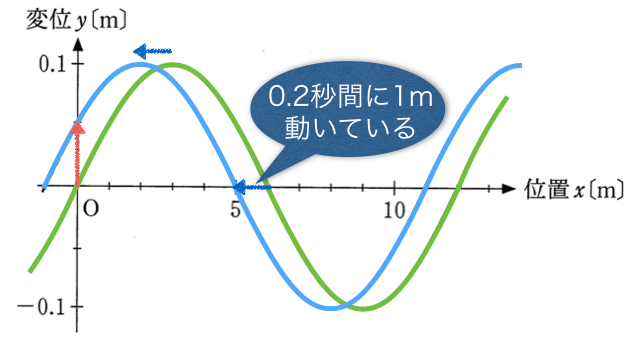
グラフから波長は分かったけど、求めたいのはこの波の速度だね。波を色分けして、緑色の波形は

=0s、水色の波形は

=0.2sの波形だ。
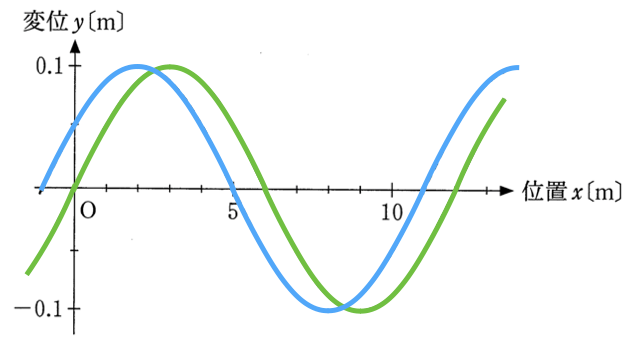
水色の方が0.2s後なんだから、例えば

=3mのところの緑色の山は、左に動いたっていうことよね。
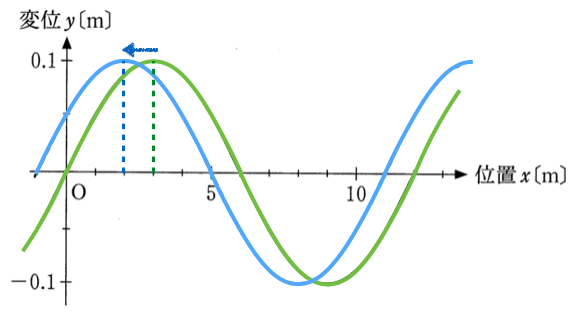
そうとも限らないよ。波って同じ形が続くから、いろんな可能性が考えられるんだ。例えば、こんな風に右に動いている可能性もあるよね。
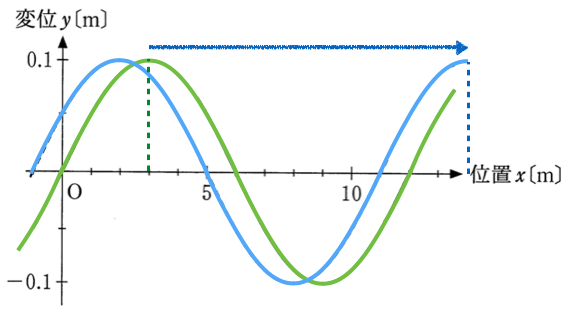
他にもさらに1波長分とか、2波長分動いて、水色の波形になっている可能性もあるから、いくらでも考えられるんだ。
ヒントっぽいのは、最後の説明かな?「媒質の変位
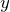
は単調に増加した。」っていうところ?
そうだよ。例えば、緑色の波形は原点Oを通っているけど、その点は時間が経つとどっちに動く?
そうだね。媒質は上下方向、つまり
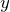
軸の方向に振動して、波は左右方向、つまり

軸の方向に進むんだよね。それでは、波がさっきのこの図のように動いたとき、原点Oはどう動く?

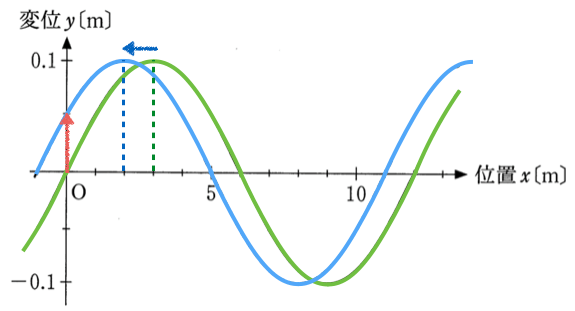

ちょっとややこしいけど、下がって、上がって、また下がってこの図かな?
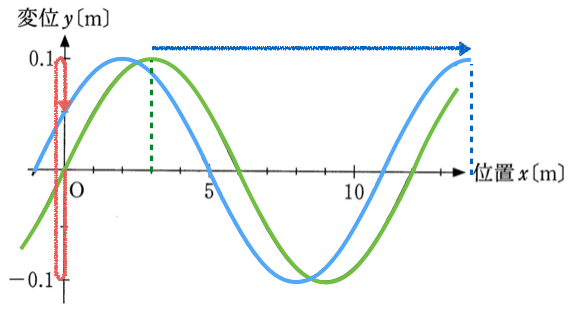
なかなか難しかったんだけど、合ってるよ。他にも考えられるけど、さらに複雑になるからやめておこう。問題文に戻って、「変位
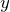
単調に増加した。」っていうのは、どういうことだと思う?
「単調に増加」っていうのは、下がった後に上がる、みたいなことはなくて、単純に上がるだけっていうことね。ということは最初のこれでしょ。

そういうことだね。それじゃあ、速度はどうなるかな?
緑のグラフに対して水色のグラフは0.2s経っていて、左に1m進んでいるから、
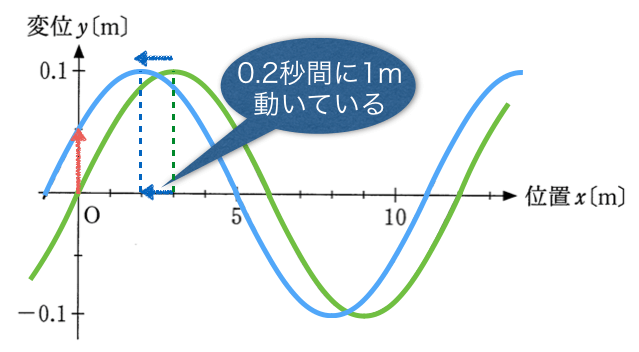
左に進んでいるから、マイナスを忘れないようにして、
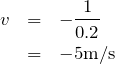

波長と速さが分かっているから、計算で求められそうね。

求めたいのは

ね。まずは2つの式から
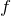
を消去して、
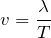
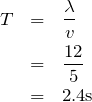


![]() か
か![]() かを確認することが大切なのよね。
かを確認することが大切なのよね。![]() だね。横軸が
だね。横軸が![]() のグラフからは何が分かるんだっけ?
のグラフからは何が分かるんだっけ?![]() のグラフは、ある時刻の波形を表しているんだから、波長が分かるのね。
のグラフは、ある時刻の波形を表しているんだから、波長が分かるのね。

![]() =0s、水色の波形は
=0s、水色の波形は![]() =0.2sの波形だ。
=0.2sの波形だ。
![]() =3mのところの緑色の山は、左に動いたっていうことよね。
=3mのところの緑色の山は、左に動いたっていうことよね。

![]() は単調に増加した。」っていうところ?
は単調に増加した。」っていうところ?![]() 軸の方向に振動して、波は左右方向、つまり
軸の方向に振動して、波は左右方向、つまり![]() 軸の方向に進むんだよね。それでは、波がさっきのこの図のように動いたとき、原点Oはどう動く?
軸の方向に進むんだよね。それでは、波がさっきのこの図のように動いたとき、原点Oはどう動く?



![]() 単調に増加した。」っていうのは、どういうことだと思う?
単調に増加した。」っていうのは、どういうことだと思う?

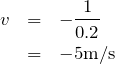


![]() ね。まずは2つの式から
ね。まずは2つの式から![]() を消去して、
を消去して、![]()