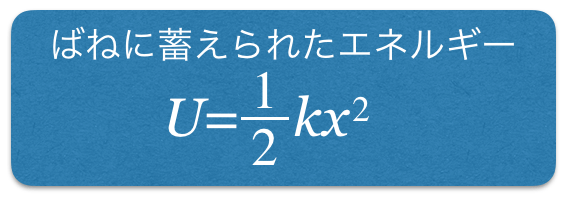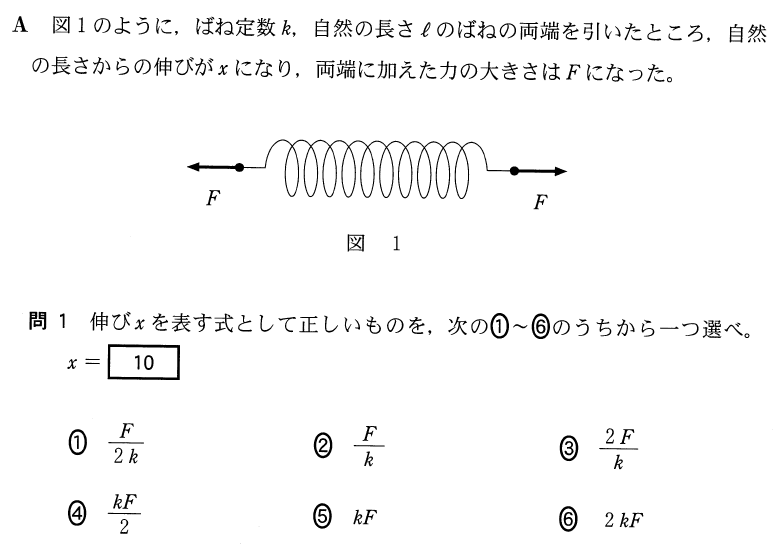

![]() で、ばねの伸びが
で、ばねの伸びが![]() だから右辺はそのままね。問題は左辺かな。右からも左からも
だから右辺はそのままね。問題は左辺かな。右からも左からも![]() で引っ張られているから、合わせて
で引っ張られているから、合わせて![]() でいいのかな。
でいいのかな。
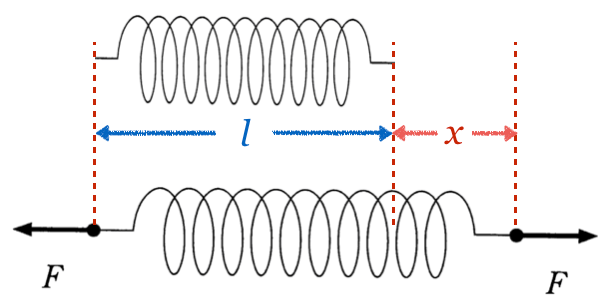
![]() になるのかな?
になるのかな?
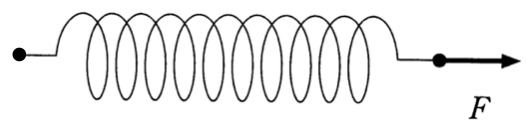
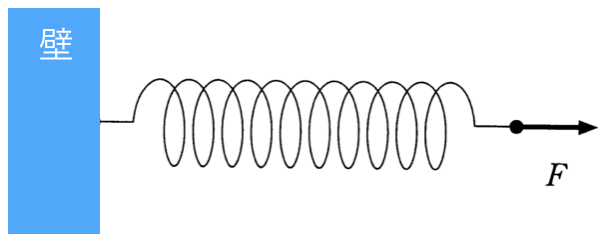
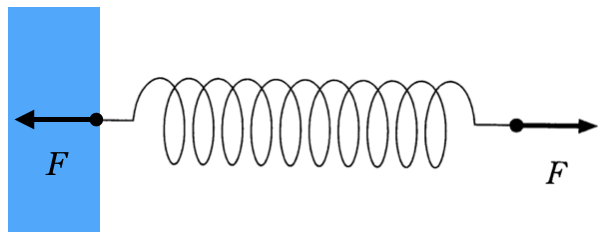
![]() ということなんだよ。
ということなんだよ。
![]() ではなく、
ではなく、![]() っていうことね。結局フックの法則の式そのままね。
っていうことね。結局フックの法則の式そのままね。
![]()
![]()

![]() かな?でも問題文に「両端に加えた力」って書いてあるから、
かな?でも問題文に「両端に加えた力」って書いてあるから、![]() かな?
かな?
![]() のままっていうわけじゃないよね。
のままっていうわけじゃないよね。
![]() だけ伸びたときに
だけ伸びたときに![]() になったということね。
になったということね。
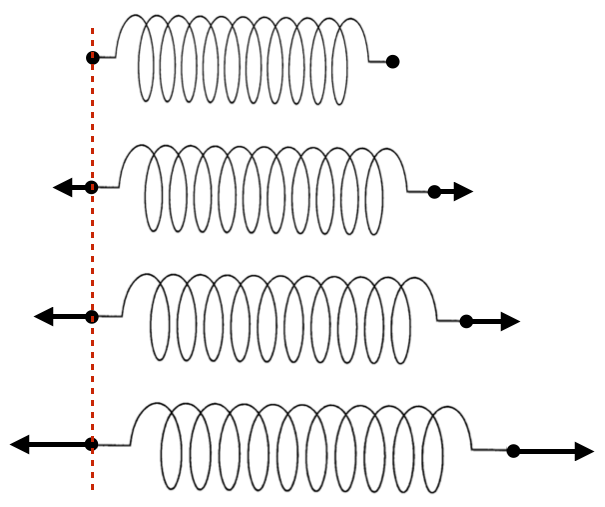


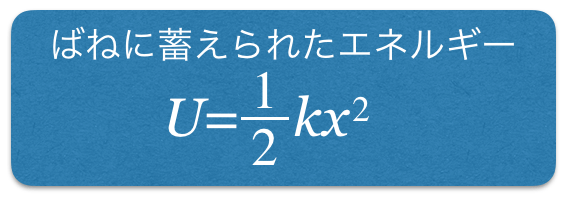
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() で、ばねの伸びが
で、ばねの伸びが![]() だから右辺はそのままね。問題は左辺かな。右からも左からも
だから右辺はそのままね。問題は左辺かな。右からも左からも![]() で引っ張られているから、合わせて
で引っ張られているから、合わせて![]() でいいのかな。
でいいのかな。

![]() になるのかな?
になるのかな?



![]() ということなんだよ。
ということなんだよ。
![]() ではなく、
ではなく、![]() っていうことね。結局フックの法則の式そのままね。
っていうことね。結局フックの法則の式そのままね。
![]()
![]()

![]() かな?でも問題文に「両端に加えた力」って書いてあるから、
かな?でも問題文に「両端に加えた力」って書いてあるから、![]() かな?
かな?
![]() のままっていうわけじゃないよね。
のままっていうわけじゃないよね。
![]() だけ伸びたときに
だけ伸びたときに![]() になったということね。
になったということね。