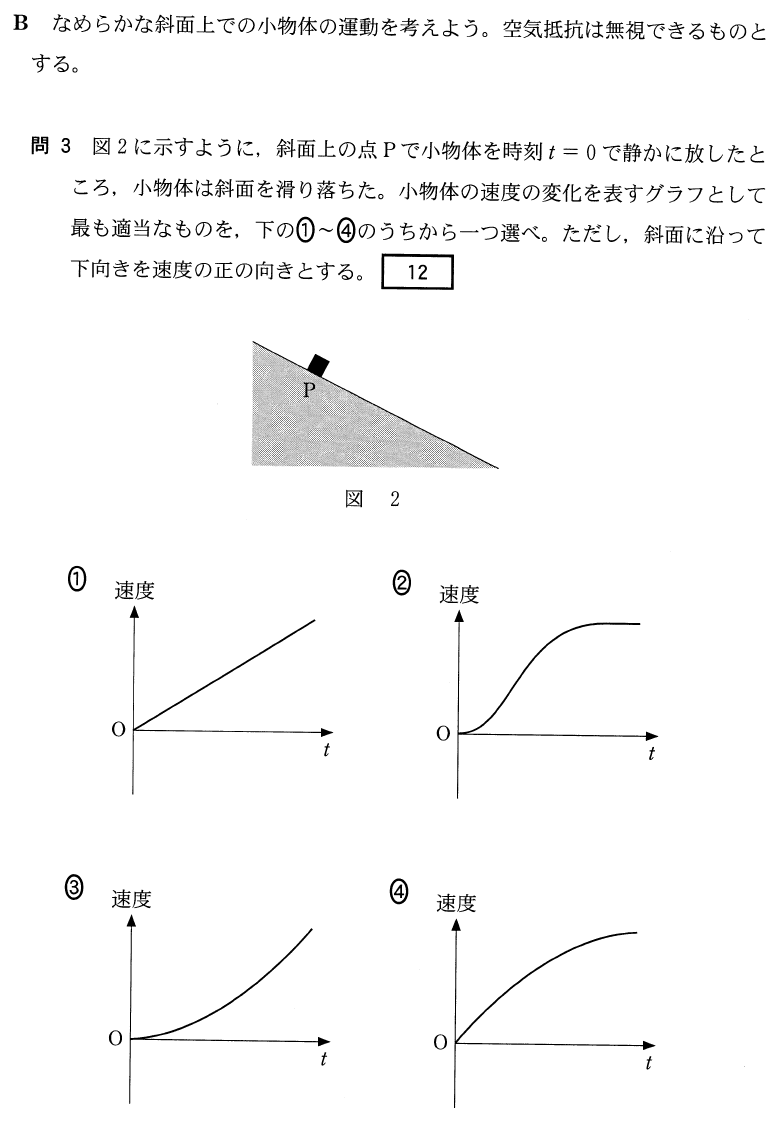
ポイントさえ理解すればそんなに難しくはないんだけどね。まず、縦軸が速度で横軸が時間のv-tグラフからは、何が分かるんだっけ?
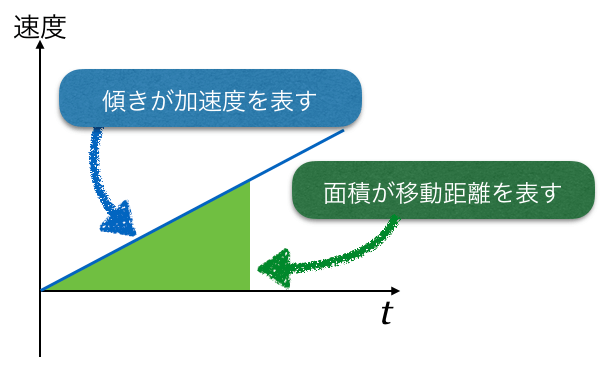
そうだね。そこまで分かっていれば十分だよ。それじゃあ、斜面上の小物体にはたらいている力はどんな力があるかな?
重力がはたらいていて、斜面から垂直抗力を受けるわね。あとは「なめらかな斜面」とあるから摩擦も無いし、「空気抵抗は無視できる」とも書かれているから、他に小物体にはたらく力は無いわね。
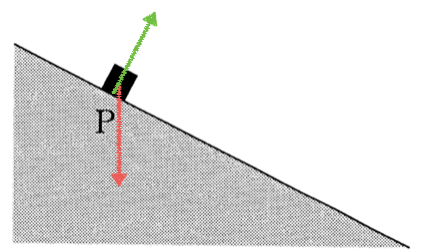
その通りだね。それじゃあ、加速度はどうなるかな?一般的な文字を使って表してみようか。
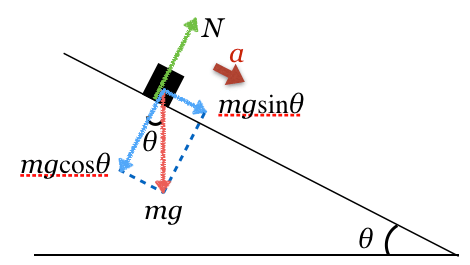
加速度を求めるなら、斜面下向きを正として運動方程式を立てればいいわね。
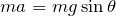
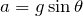
ということは、
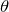
は変化しないから、加速度は一定だよね。
「等加速度」ということは、グラフでいうとどういうこと?
v-tグラフの傾きが加速度だから、等加速度だと「傾きが一定」ということね。ということは、グラフでいうと①ということね。
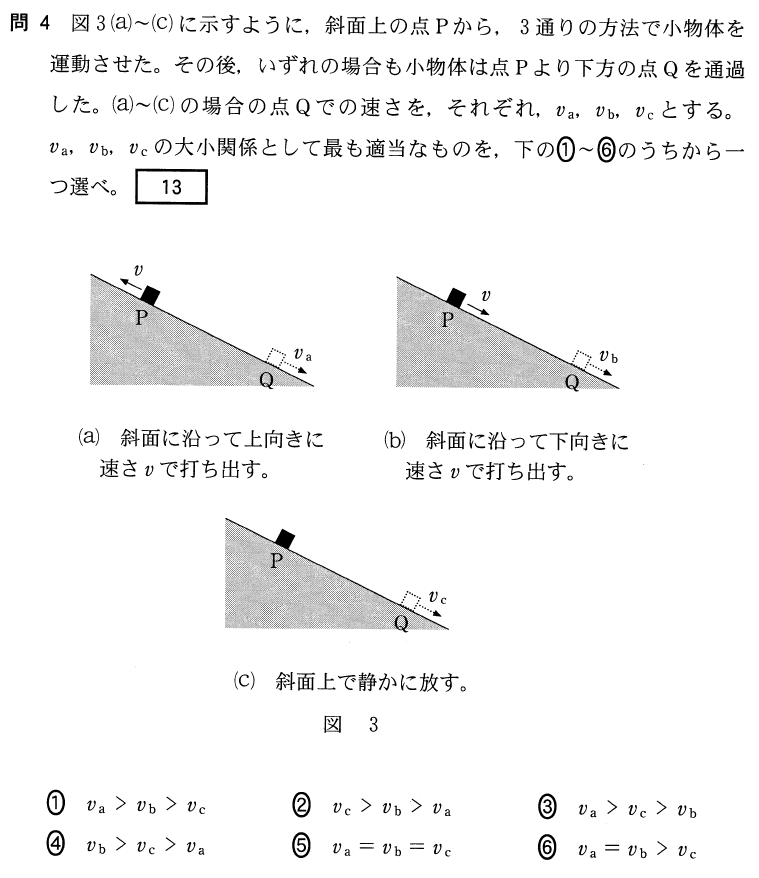
点Qで最も速いのは、図から判断するとどれだと思う?
(b)かな。最初から下向きの速さを持っているから、点Qだともっと速くなるっていうことよね。
(a)は点Qとは逆向きの初速度だから、遅いんじゃないかな。
(a)のとき、点Pに戻ってきたときの速さは分かるかな?
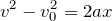
を使うと、同じ高さに戻ってきたとき、

=0だから、
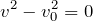
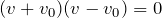
今の場合、

と
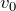
は逆向きだから、
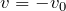
になるわね。ということは、戻ってきたんだから向きが逆なのはいいとして、初速度と同じ速さになっているっていうことね。そう言われれば、鉛直投射のところでも戻ってきたときには同じ速さになるって聞いたことがあるわ。
そうなんだよ。鉛直投射と同じで、斜面でも摩擦がなければ、斜面上方に打ち出された物体は、戻ってきたときには同じ速さになってるんだ。
ということは、(a)のとき、点Qに達したときには(b)と同じ速さになっているということね。
そうなんだよ。なので答えは⑤か⑥だね。(c)はどうかな?
(c)は点Pでの速さが0なので、明らかに(a)や(b)より遅いでしょ。だから答えは⑥ね。
そうだね。ちゃんと計算するとすると、この問題は力学的エネルギー保存則を考えると一発で答えがでるんだよ。
等加速度直線運動の式を使うんじゃなくて、力学的エネルギー保存の法則なのね。
そうなんだ。点Qを重力による位置エネルギーの基準として、点Pの高さを
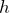
とするよ。あとは力学的エネルギー保存の法則の式を立ててみるよ。
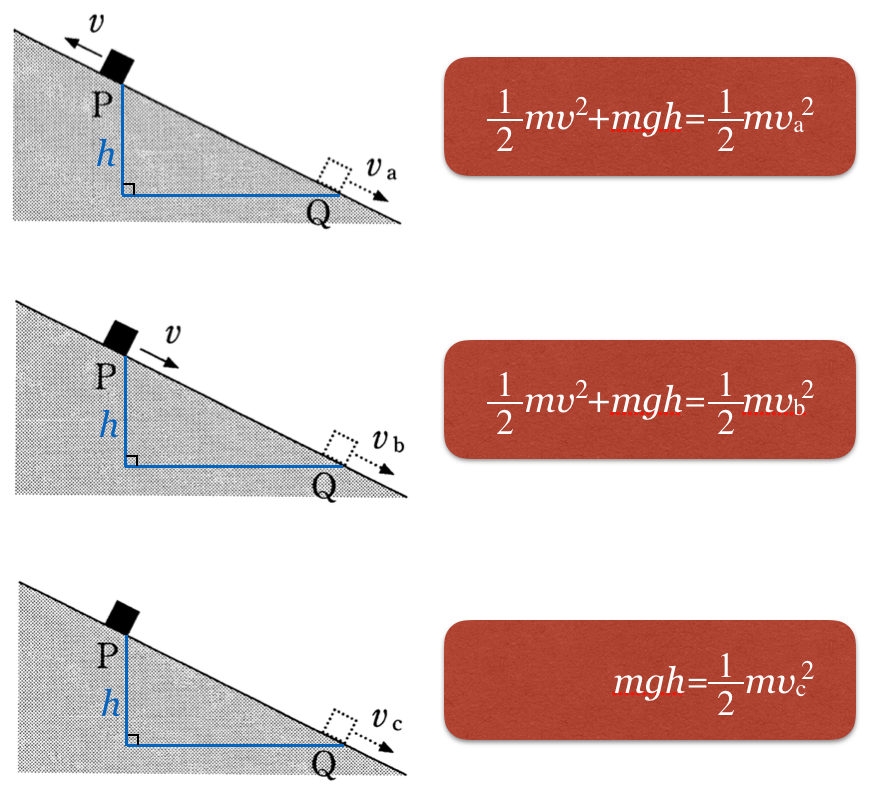
なるほどね。3つの式を並べてみると、
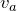
と
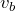
は同じで、
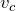
はそれよりも小さいことは一目瞭然ね。




![]()
![]()
![]() は変化しないから、加速度は一定だよね。
は変化しないから、加速度は一定だよね。
![]()
![]() =0だから、
=0だから、![]()
![]()
![]() と
と![]() は逆向きだから、
は逆向きだから、![]()
![]() とするよ。あとは力学的エネルギー保存の法則の式を立ててみるよ。
とするよ。あとは力学的エネルギー保存の法則の式を立ててみるよ。
![]() と
と![]() は同じで、
は同じで、![]() はそれよりも小さいことは一目瞭然ね。
はそれよりも小さいことは一目瞭然ね。 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!



![]()
![]()
![]() は変化しないから、加速度は一定だよね。
は変化しないから、加速度は一定だよね。
![]()
![]() =0だから、
=0だから、![]()
![]()
![]() と
と![]() は逆向きだから、
は逆向きだから、![]()
![]() とするよ。あとは力学的エネルギー保存の法則の式を立ててみるよ。
とするよ。あとは力学的エネルギー保存の法則の式を立ててみるよ。
![]() と
と![]() は同じで、
は同じで、![]() はそれよりも小さいことは一目瞭然ね。
はそれよりも小さいことは一目瞭然ね。