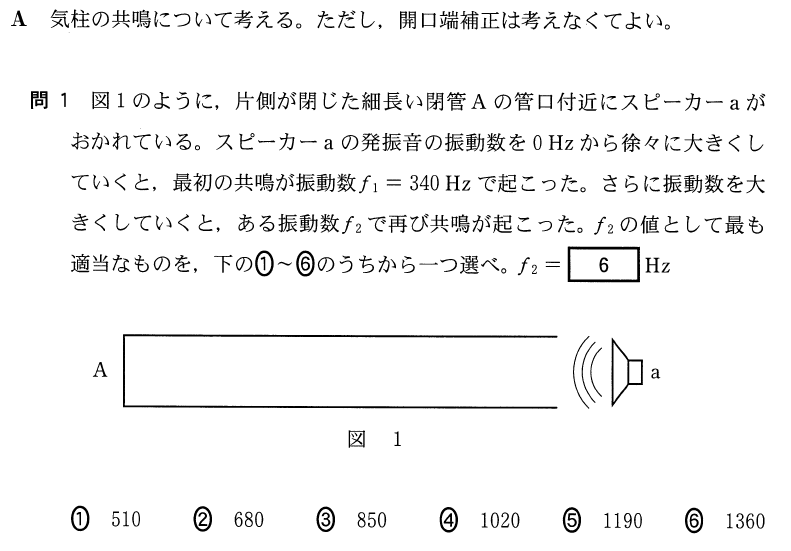

![]() としておこうか。
としておこうか。
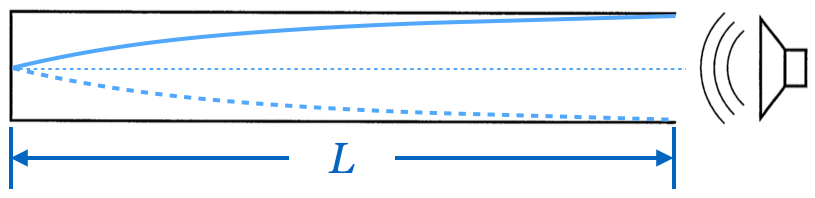
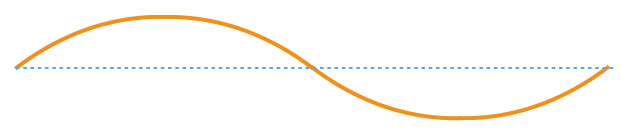
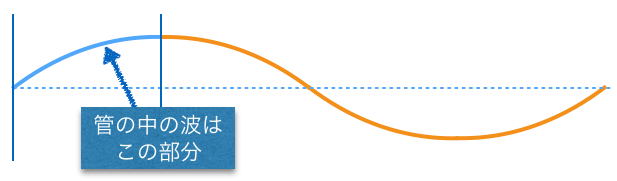
![]() だとすると、
だとすると、
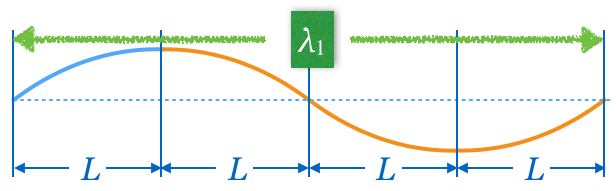
![]()
![]() も求めてみようか。
も求めてみようか。

![]() とすると、
とすると、
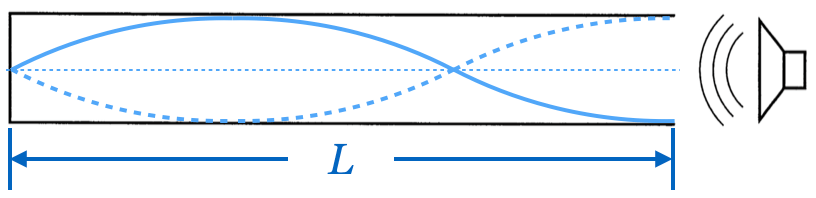
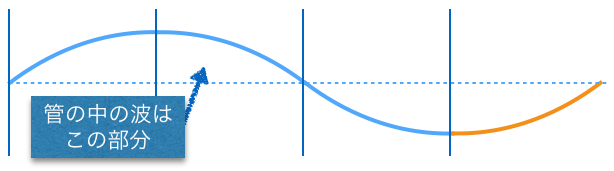
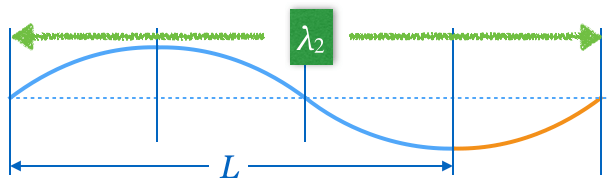
![]() は、
は、
![]()
![]() なんだけど、どうやって求めようか。
なんだけど、どうやって求めようか。

![]() は同じなので、
は同じなので、
![]()
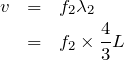
![]() を消去すると、
を消去すると、
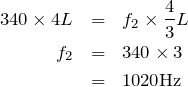
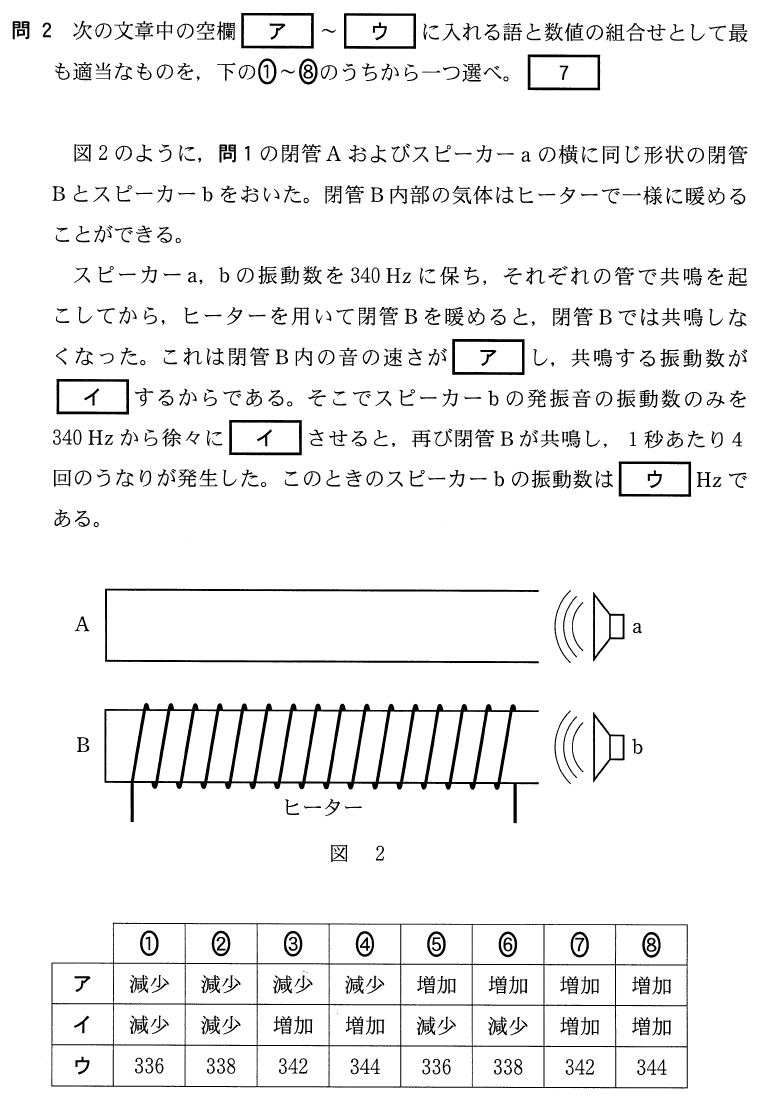
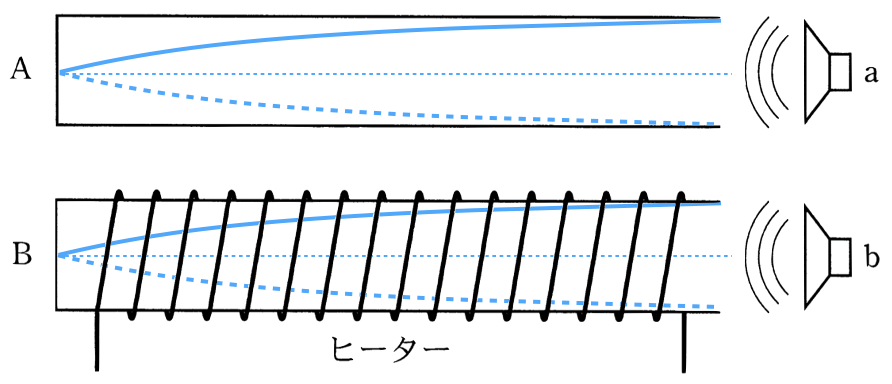
![]() で決まるんだよね。
で決まるんだよね。

![]() が大きくなって、
が大きくなって、![]() は変わらないから、
は変わらないから、![]() なので
なので![]() も大きくなるっていうことね。空欄は[ア]も[イ]も「増加」が入るのね。
も大きくなるっていうことね。空欄は[ア]も[イ]も「増加」が入るのね。
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() としておこうか。
としておこうか。



![]() だとすると、
だとすると、

![]()
![]() も求めてみようか。
も求めてみようか。

![]() とすると、
とすると、



![]() は、
は、
![]()
![]() なんだけど、どうやって求めようか。
なんだけど、どうやって求めようか。

![]() は同じなので、
は同じなので、
![]()
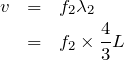
![]() を消去すると、
を消去すると、
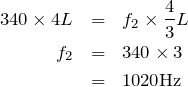


![]() で決まるんだよね。
で決まるんだよね。

![]() が大きくなって、
が大きくなって、![]() は変わらないから、
は変わらないから、![]() なので
なので![]() も大きくなるっていうことね。空欄は[ア]も[イ]も「増加」が入るのね。
も大きくなるっていうことね。空欄は[ア]も[イ]も「増加」が入るのね。