動画解説をYouTubeにUPしました。動画での解説と、このサイトでの解説を少し変えましたので、ぜひどちらも参考にしてください
コンデンサーは少しできそうな気がする。だいたい
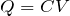
を使えば問題が解けるでしょ。
大体解けるかどうかは別として、
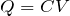
は必ずと言っていいほど使うよね。じゃあ、まず左のコンデンサーにかかっている電圧と、右のコンデンサーにかかっている電圧を求めてよ。
もちろん
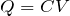
を使うのね。左のコンデンサーは
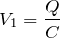
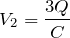
ということは、左のコンデンサーと右のコンデンサーの電圧は違うっていうことだよね。
いやいや。おかしくはないんだよ。スイッチが開いているので、電圧が違っても全く問題ないよ。じゃあ、スイッチを閉じたらどうなるかな？
そうなると少し難しいのよね。でもこの問題は、きっとスイッチを閉じると右のコンデンサーにたまっている電荷が、左のコンデンサーに移動すると思うわ。明確な理由はわからないけど、そんな気がする。
その勘は合ってるよ。とにかくまず電荷が移動するんだ。移動する向きはこう考えるんだ。
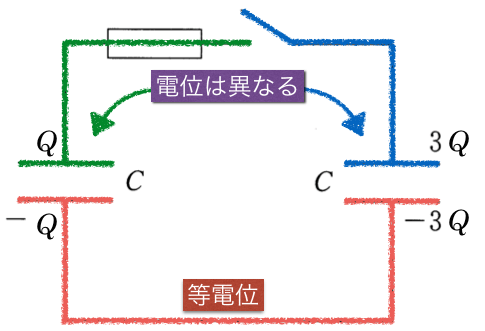
図の下側の赤く線を引いた部分は等電位なんだ。金属が繋がっていれば、どこでも電位が等しいんだよね。
電位の考え方って苦手なんだけど、そこまでは分かるわ。
図の上側は、スイッチが開いているので、金属的に繋がっていないね。だから別の電位になるんだ。さっき求めた２つのコンデンサーにかかっている電圧が異なるのは、これが理由なんだ。
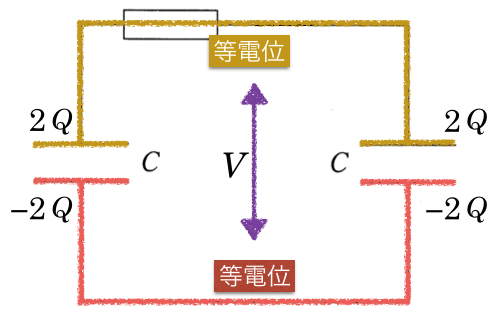
抵抗に電流が流れている間は抵抗の両端に電位差が生じているけど、電荷の移動が終わって抵抗に電流が流れていなければ、図の上側の部分も等電位になるんだ。つまり、スイッチを閉じると、２つのコンデンサーにかかる電圧が等しくなるように、電荷が動くっていうことだね。
左右のコンデンサーの電荷が等しくなるように動くんじゃないの？
そう、違うんだよ。この問題では、２つのコンデンサーの電気容量がどちらも
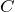
で、電圧が等しいので、
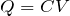
を用いると、電気量も等しくなるけど、
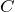
が違えば、電気量も違ってくるんだね。
そうなんだ。蓄えられている電気量は、単純に平均すればいいの？
電気容量
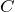
が等しければそれでOKだね。一般的にはコンデンサーそれぞれについて
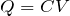
の式を立てて、電気量保存の法則を使えば計算できるよ。今はまだ続きがあるから先に進むよ。
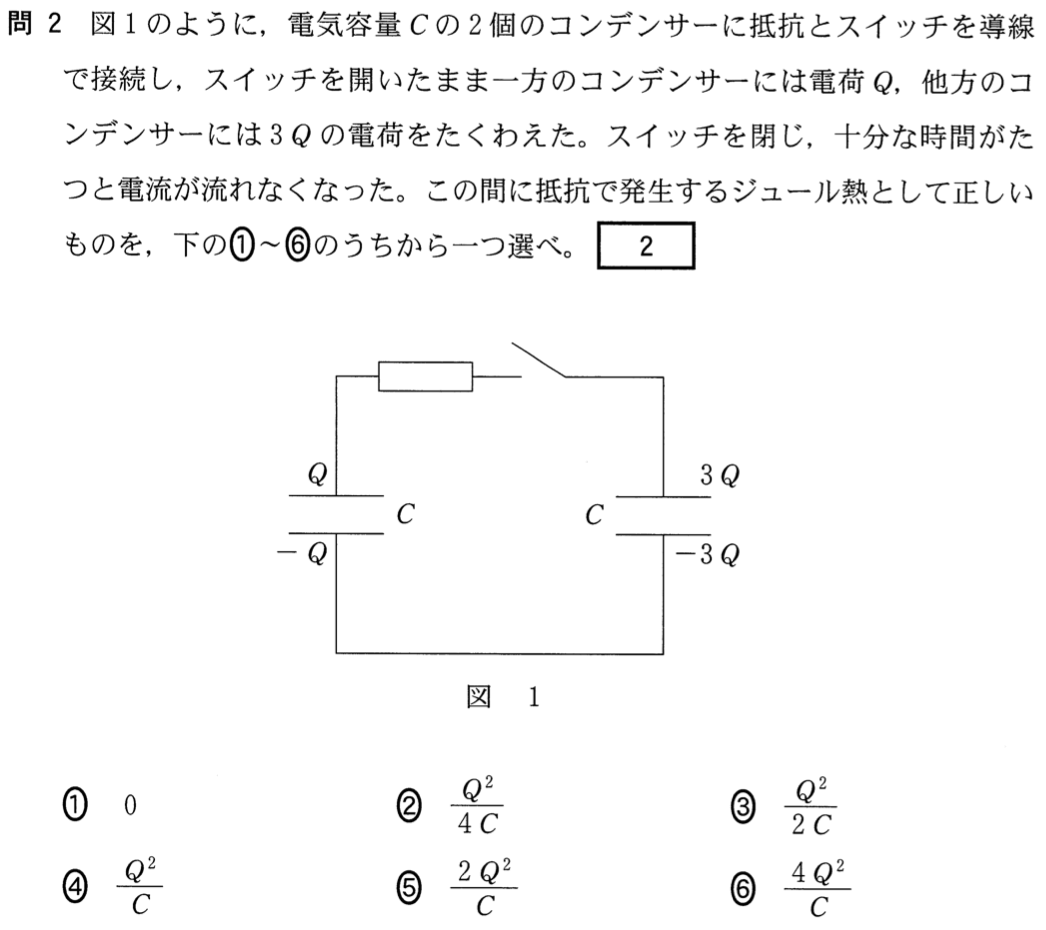
そうしましょう。この問題で求めたいのは、電気量じゃなくて抵抗で発生するジュール熱ね。
えっ、そうなの？抵抗で発生するジュール熱と、コンデンサーに蓄えられている電気量が関係あるの？
それがあるんだな。物理の問題ではよくあるでしょ。「Ａを求めよ」という問題なのに、Ａを直接求めることはできなくて、別のＢを求めると、その結果Ａが分かるっていうこと。
そうかもしれないね。ジュール熱の公式って知ってる？
ジュール熱のあたりもなんだか式が多くて、あんまり覚えていないよ。でも確か
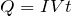
だったような･･･
正解！よく覚えていたね。じゃあ、その式を使えば求まるかな？
だって分からないんだよ。抵抗で発生するジュール熱を求めたいんだから、この式でいう
は抵抗の両端にかかる電圧だよ。コンデンサーにかかる電圧ではないんだ。
いずれにしても、公式からジュール熱を求めることは無理だ。じゃあ、別の方法を考えよう。ジュール熱の単位は何だか分かる？
その通り！じゃあ、他に単位がＪの物理量って何か知ってる？
それは覚えているわ。単位がＪなのは、「熱」、「エネルギー」、「仕事」ね。
そうだよ。この問題ではジュール熱を「熱」としては計算できなかったよね。あと「仕事」もこの場合は使えなさそう。ということは、「エネルギー」を考えてみよう。コンデンサーに蓄えられているエネルギーは、どうやって求めるか知ってる？
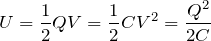
を求めちゃえば、どれでも良さそうね。
そうなんだけど、さっき
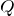
を求めたし、答えの選択肢を見ると、どれも
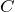
と
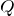
からできているから、一番最後の式
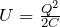で考えてみよう。最初の図で、それぞれのコンデンサーに蓄えられているエネルギーを求めるとどうなるかな？
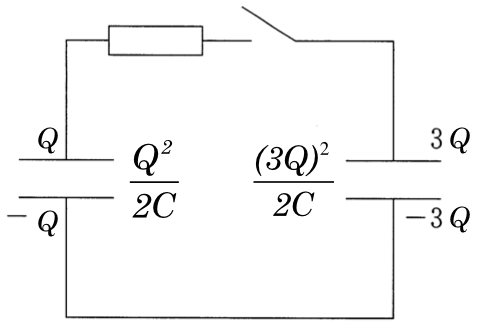
すでに
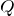
が求まっているから、簡単！
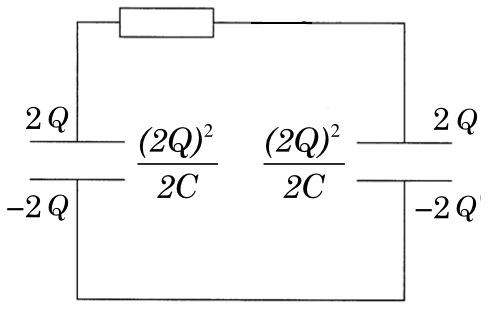
ここまでは簡単なんだけど、これと抵抗で発生するジュール熱と、どう関係があるの？
計算をしてみると分かるんだけど、スイッチを閉じる前と後で、コンデンサーに蓄えられているエネルギーの和が減ってるんだ。で、その減った分がどこへ行くかというと･･･
それが抵抗で発生するジュール熱になるってことね。他にエネルギーが消費される場所が無いもんね。
そういうことだね。
スイッチを閉じる前にコンデンサーに蓄えられているエネルギーの和
||
スイッチを閉じた後にコンデンサーに蓄えられているエネルギーの和
＋
抵抗で発生するジュール熱
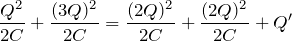
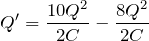
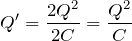
タイトルとURLをコピーしました
も
もよく分からないわ。
