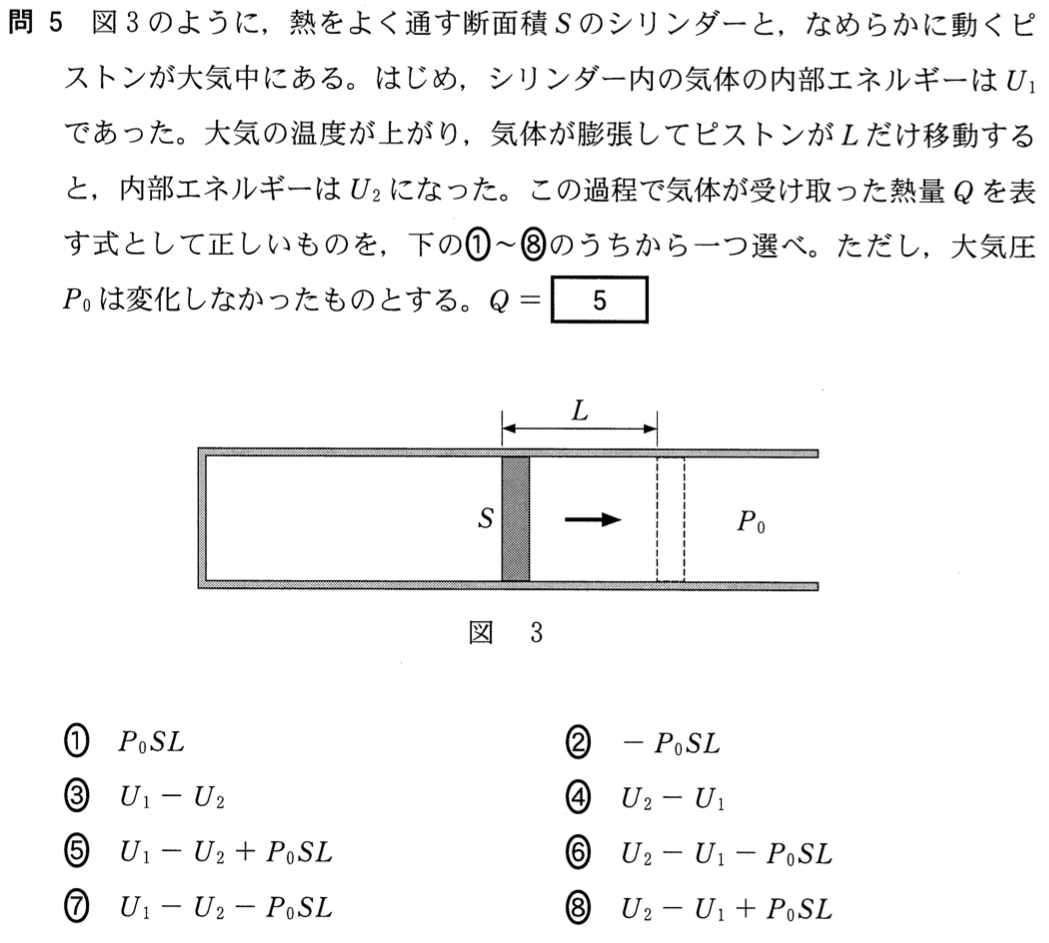
熱の問題ね。どうすればいいのか、あんまり分からない。
まずは、圧力
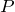
、体積

、絶対温度

の変化を読み取ろう。まず、圧力はどうなるかな?
この状況で分かる、ということは
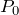
ということ?
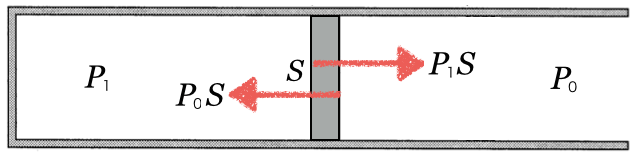
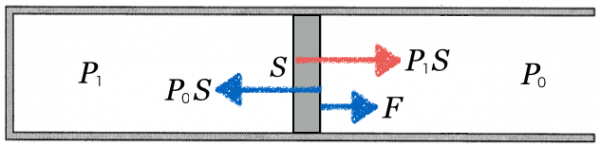
真ん中にあるピストンはたらく左右方向の力を考えるよ。どんな力がはたらいている?
すばらしい!正解だよ。でもそれ以外は考えられないもんね。ピストンとシリンダーの間に摩擦があると、摩擦力も考えられるけど、問題文に「なめらかに動くピストン」って書いてあるから、摩擦はないよね。
「なめらか」って書いてあるのは、そういうことなのね。
そうだね。中の気体の圧力を
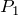
としてみよう。「圧力×面積=力」でしょ。左右方向を考えると、中の気体が押す力と外の気体が押す力がつり合っているんだね。
そうか!
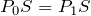
なので、中の圧力も大気圧と同じ
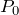
なのね。
これは簡単。断面積と長さをかければいいから、
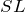
だけ体積が増えているわね。
そうだね。最後は絶対温度。温度は書いていないけど、上がったか、下がったかだけなら分かるよね。
「大気の温度は上がり」って書いてあるわ。これって中の温度も上がっていうこと?
そういうことだね。問題文に「熱をよく通す〜シリンダー」って書いてあるからね。
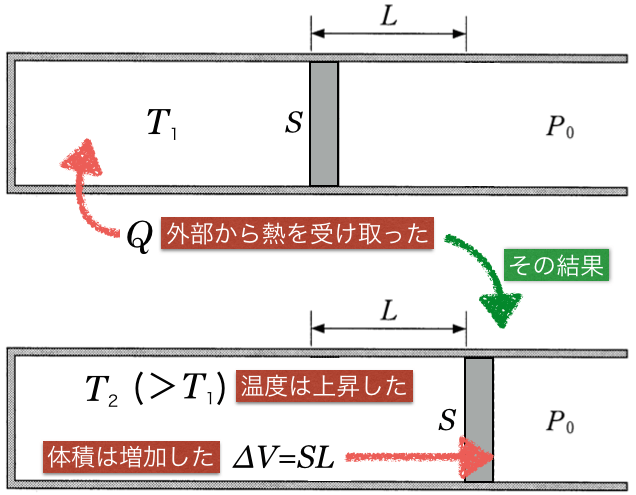
さぁて、そこまで確認したら、次は「熱力学第1法則」だね。問題によっては「ボイル・シャルルの法則」や、「理想気体の状態方程式」を使ったりするんだけど、この問題は熱力学第1法則だね。
確かに「内部エネルギー」が出てきたり、「熱量」を求めたいんだから、「熱力学第1法則」を使いそうな気はする。でも苦手なのよ、「熱力学第1法則」。だって、公式が2つあるでしょ。
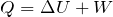
っていうのと、
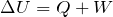
っていうやつ。この2つの式は符号が違うでしょ。意味が分からないわ。
もちろん「熱力学第1法則」は1つしかないんだけど、表し方が2種類あるっていうことだね。どちらか一方だけをマスターすれば大丈夫なんだけど、場合によって使い分けられるともっと理解が深まると思うよ。大切なのは、どう変化したかなんだ。熱の出入り、温度の上昇下降、体積の増減の3つだ。この問題ではどう?
熱は入ってくるわね。温度は上昇、体積は増加ね。それだけ分かればいいの?
そうだよ。この問題では、「外から熱が入ってきた結果、温度が上昇して、体積が増えた」ということだよね。ということは
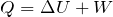
と考えればいいんだ。
熱の出入りはいいとして、温度の上昇が内部エネルギーと関係していて、体積の増加が仕事と関係しているということ?
その通り!まず内部エネルギーは絶対温度に比例するんだ。だから温度上昇はそのまま内部エネルギーの増加になるんだ。それから、体積の増加は気体が外に仕事をしたということになるんだ。
内部エネルギーの話は分かるんだけど、気体の体積が増加したら、必ず期待は外に仕事をしたことになるの?
えー、だって、例えばピストンを右から手で引っ張ったら、中の気体は外から仕事をされたことにならないの?
ならないよ。単純に体積増加は外部に仕事をした、と考えていいんだ。敢えて説明すると、中の気体と外の大気がピストンを押しているんだけど、右から手で引っ張ると、その引く力は大気が押す力の影響を弱めているっていうイメージかな。外からの力の影響が弱まった分、中の気体が押すことができた、ということだよ。
それでは改めて熱力学第1法則の式を書くよ。この図を見ると分かりやすいかな。
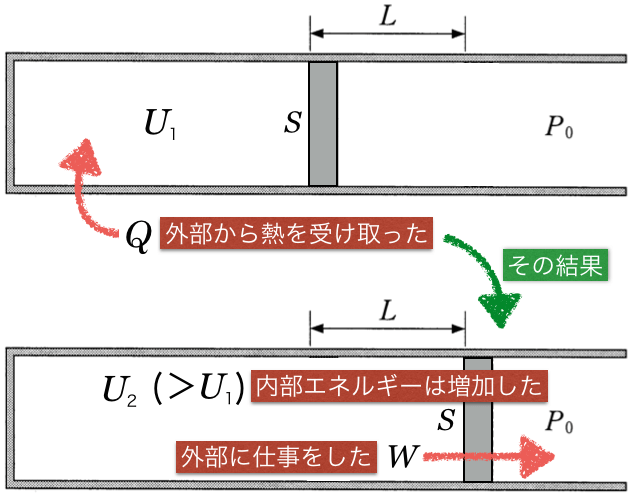
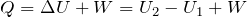
正解!でも一応外部にした仕事も求めておこうか。この時の気体の変化は、何変化って言うと思う?
等温でも断熱でもないわね。定積変化でもないから、あとは何があったっけ?あっ、定圧変化かな。
そうだね。結局内部の圧力は常に大気圧と同じなので、ずっと
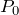
のままの定圧変化だね。
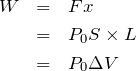
なんとなく分かったわ。熱力学第1法則の式に入れてみると
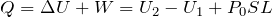
![]() 、体積
、体積![]() 、絶対温度
、絶対温度![]() の変化を読み取ろう。まず、圧力はどうなるかな?
の変化を読み取ろう。まず、圧力はどうなるかな?![]() としてみよう。「圧力×面積=力」でしょ。左右方向を考えると、中の気体が押す力と外の気体が押す力がつり合っているんだね。
としてみよう。「圧力×面積=力」でしょ。左右方向を考えると、中の気体が押す力と外の気体が押す力がつり合っているんだね。![]() と考えればいいんだ。
と考えればいいんだ。![]()
![]() のままの定圧変化だね。
のままの定圧変化だね。![]() っていう式があるんだ。これは、そもそも仕事の定義
っていう式があるんだ。これは、そもそも仕事の定義![]() から求めることができるんだ。内部の気体の圧力を
から求めることができるんだ。内部の気体の圧力を![]() とすると、
とすると、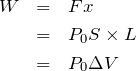
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]() 、体積
、体積![]() 、絶対温度
、絶対温度![]() の変化を読み取ろう。まず、圧力はどうなるかな?
の変化を読み取ろう。まず、圧力はどうなるかな?![]() としてみよう。「圧力×面積=力」でしょ。左右方向を考えると、中の気体が押す力と外の気体が押す力がつり合っているんだね。
としてみよう。「圧力×面積=力」でしょ。左右方向を考えると、中の気体が押す力と外の気体が押す力がつり合っているんだね。![]() と考えればいいんだ。
と考えればいいんだ。![]()
![]() のままの定圧変化だね。
のままの定圧変化だね。![]() っていう式があるんだ。これは、そもそも仕事の定義
っていう式があるんだ。これは、そもそも仕事の定義![]() から求めることができるんだ。内部の気体の圧力を
から求めることができるんだ。内部の気体の圧力を![]() とすると、
とすると、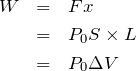
![]()