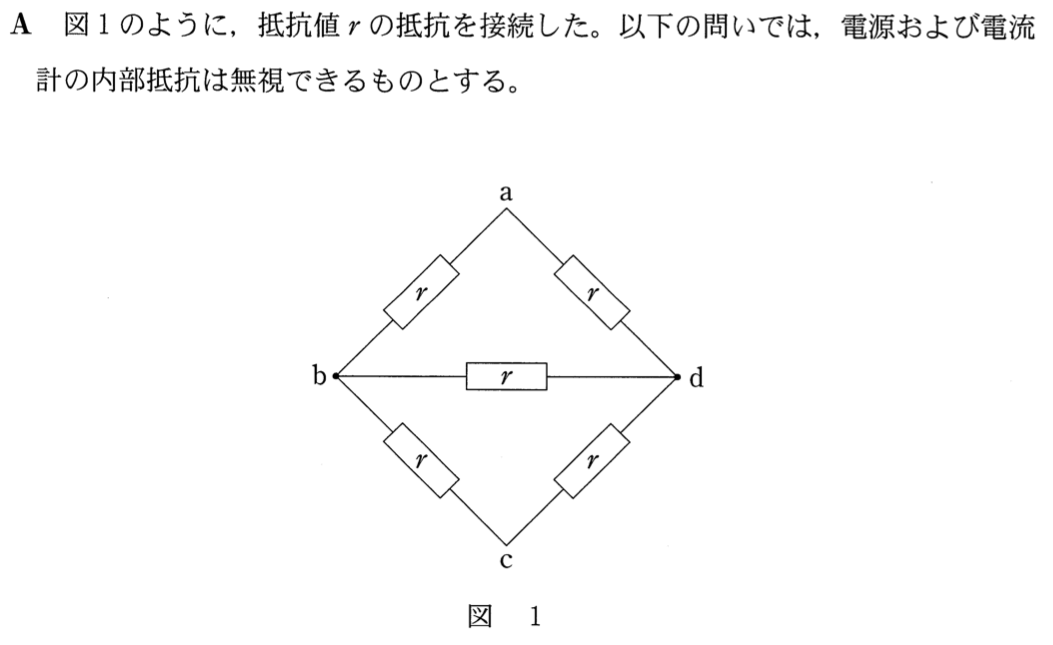
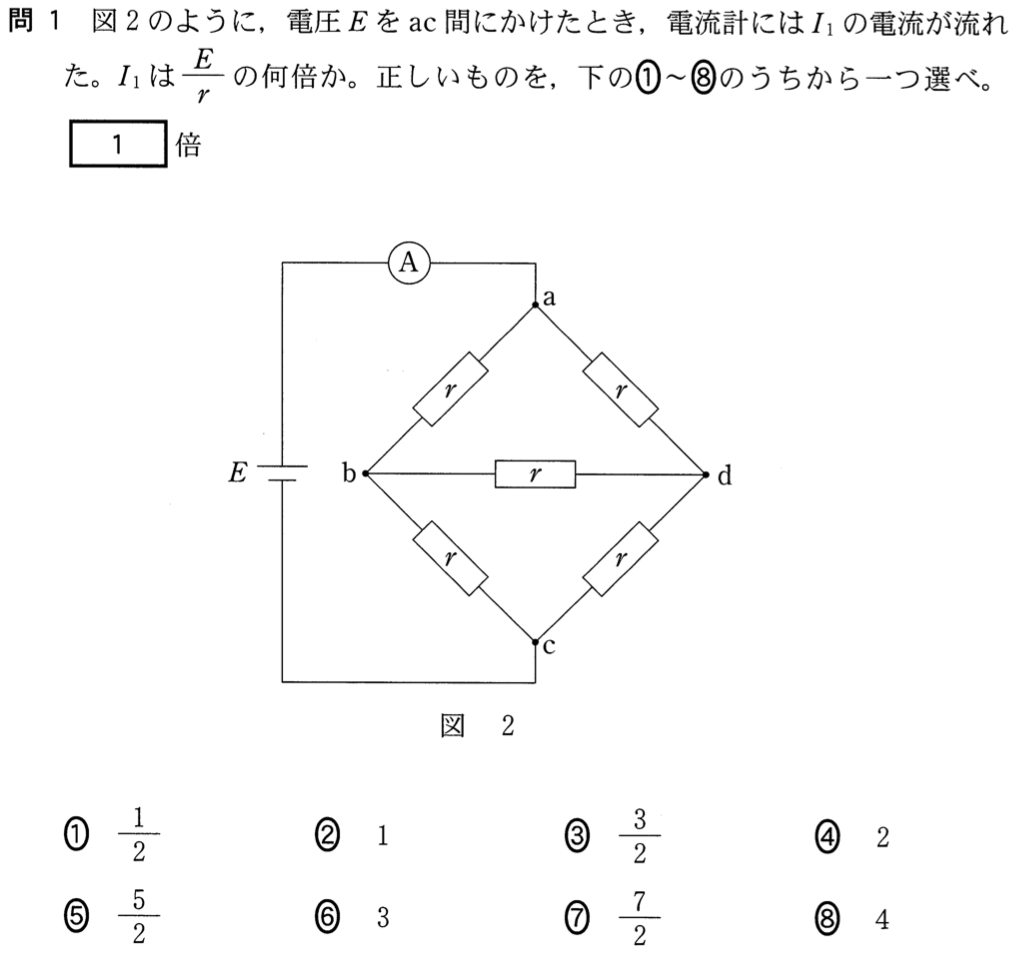
動画解説をYouTubeにUPしました。動画での解説と、このサイトでの解説を少し変えましたので、ぜひどちらも参考にしてください。
どこかで見たことがあるような回路だわ。確か、「ホイートストンブリッジ」ね。
bd間に検流計が入っているとき「ホイートストンブリッジ」って言うんだね。bd間に何もなければ、抵抗が2つずつの並列回路なんだけど、bd間に入っているために、並列回路とか、直列回路とか言えなくなるんだ。ちょうどbd間を橋渡ししている感じなので、ブリッジ回路って言うんだ。
並列回路とか、直列回路だと合成抵抗を求めることで、回路に流れる電流が求められるのよね。この問題ではブリッジ回路になっているために合成抵抗は、すぐには求められないわ。こういうときは「キルヒホッフの法則」を使うって聞いたわ。
おっ!よく分かってるね。例えば次のように電流を決めて、式を立てるんだね。
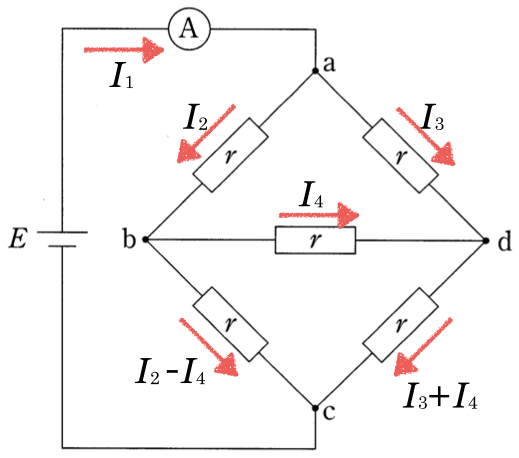
文字がいっぱいね。導かれる方程式を連立すれば解けるんでしょうけど、たいへんだわ。
そうなんだよ。キルヒホッフの法則で解けるんだけど、計算が大変なんだ。なので、電位の考え方で解けないかな?
大丈夫だよ。分かってくれると思うな。全部の抵抗が

なので、すごく簡単になるんだ。まずは等電位のところを分かりやすくするよ。
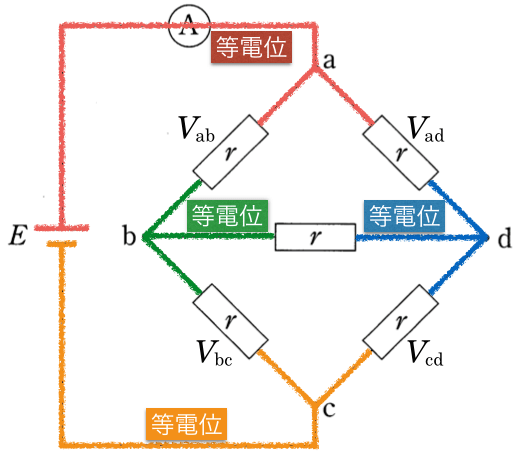
導線で繋がっているところが等電位なのよね。ここまでは分かるわ。
この回路って、全ての抵抗が

なので、抵抗の配置が左右対称になっているよね。なので、図中に書いた各抵抗の電圧を考えると、
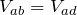
、
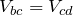
となるんだ。
抵抗が全部同じで、抵抗の配置も対称だからっていうことね。
そうだね。その結果、bの電位とdの電位が同じになるよね。
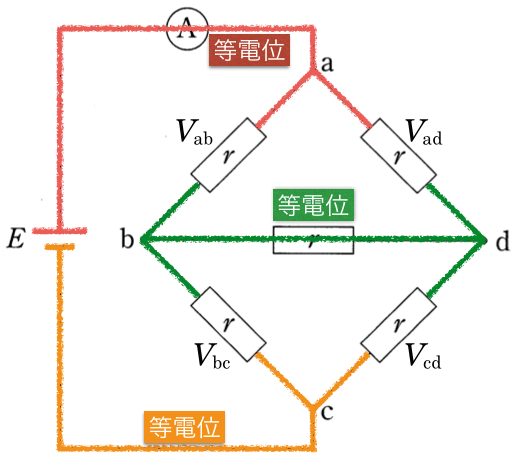
抵抗には電位の高い方から低い方へ電流が流れるのよね。だから、抵抗の両側が等電位っていうことは、電流が流れないっていうことかな?
そういうことだね。左右対称ということと、bd間には電流が流れないということを考慮すると、次のような図になるよ。
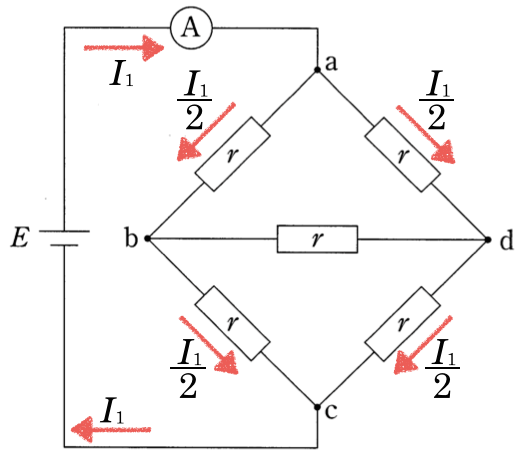
電流計に流れる電流が、a点で2つに分かれて、左右対称だからちょうど半分ずつになるということね。
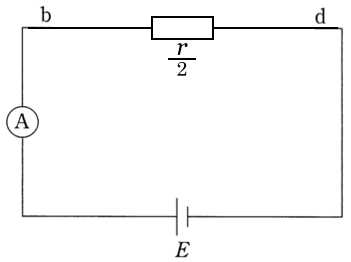
このままでもいいんだけど、もう少し簡単な回路に書き直してみるとこうなるんだ。
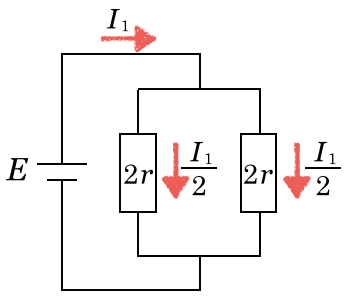

の抵抗が2つ直列に繋がっているので、
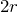
になるのね。
どちらの抵抗にもかかっている電圧は
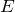
なので、オームの法則を使ってみよう。
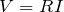
ね。
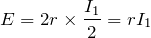
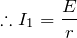
そいうことだね。答えは1倍なので②だ。では、問2にいこう。
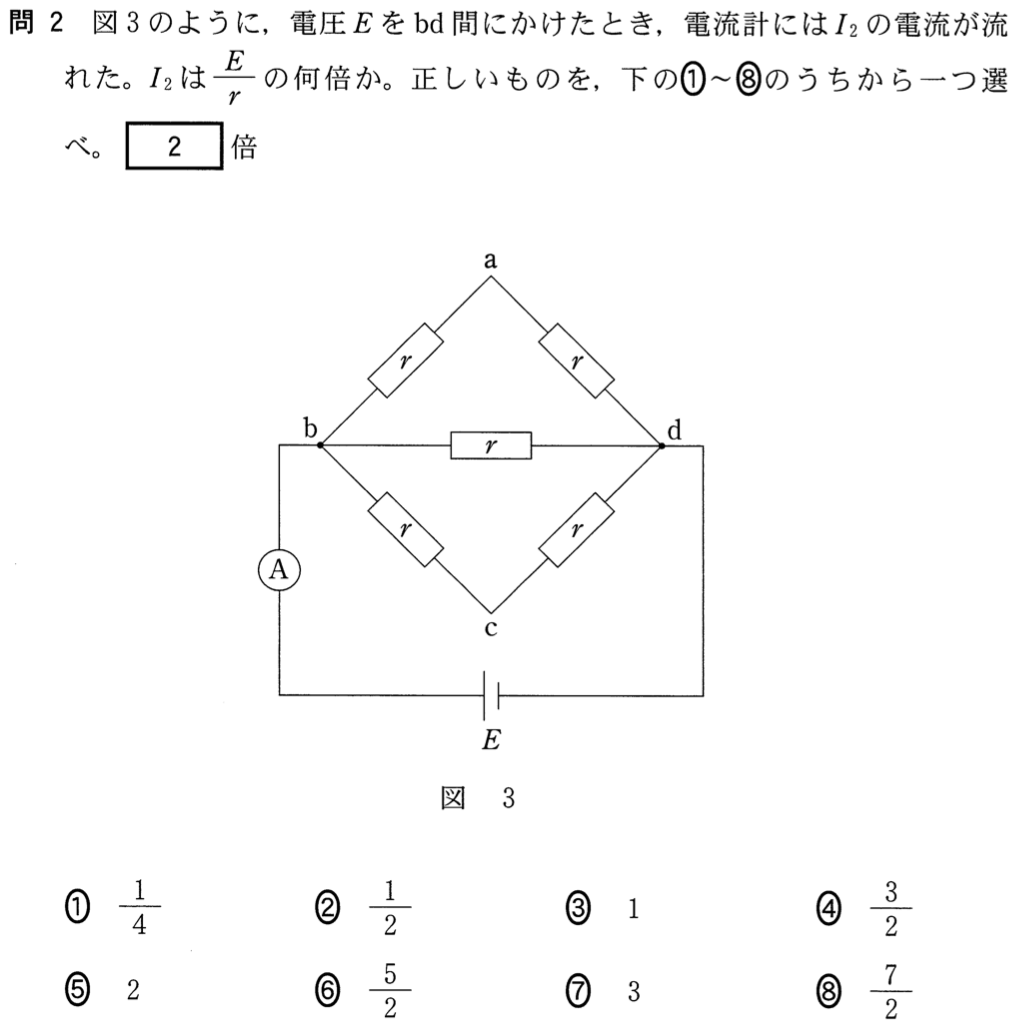
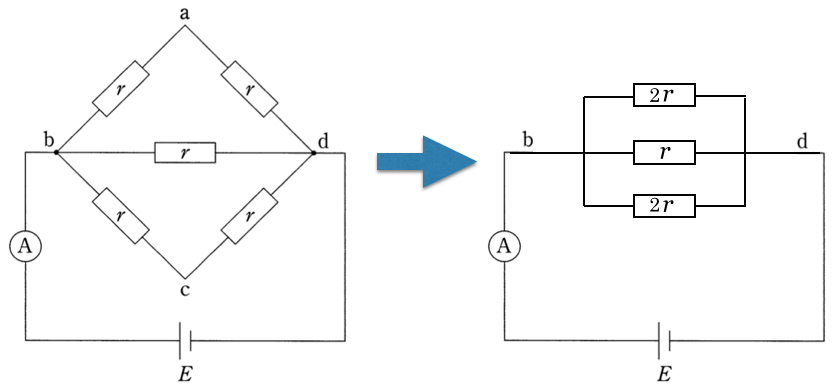
3つの抵抗の合成抵抗を
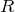
とすると、並列回路なので、
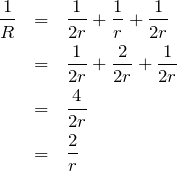
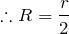
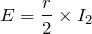
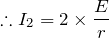
というわけで2倍になるから、答えは⑤だね。最後に問3だ。
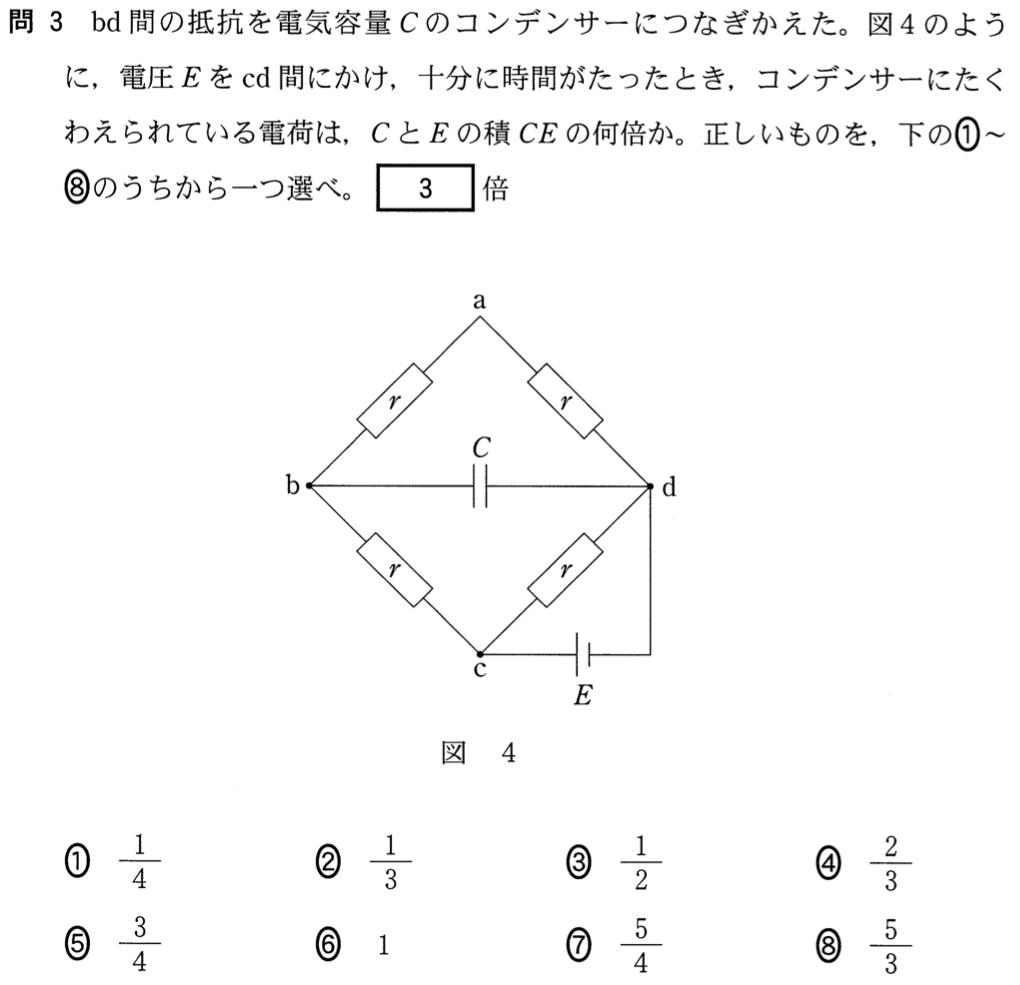
これは、なんか変なところに電圧がかかっていて、しかもコンデンサーが入ってる。難しそう!
ここまではできるわ。今はコンデンサーに蓄えられている電荷が必要なので、
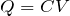
は使うわよね。
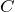
は与えられているから、

を求めればいいわね。
コンデンサーにかかる電圧は、すぐには求められないので、まずは「十分時間がたったとき」のc→b→a→dに流れる電流
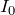
を求めよう。
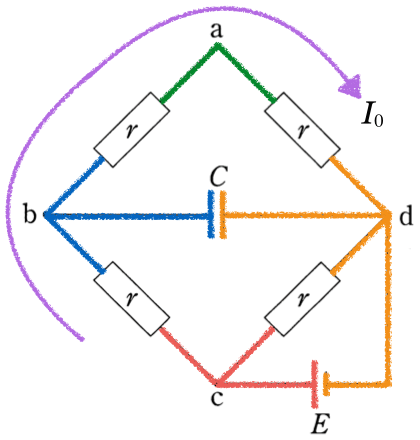
「十分時間がたった」というのは、コンデンサーに電流が流れなくなったときよね。なので直列に接続された3つの抵抗に電圧
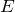
を接続したのと同じね。ということは、合成抵抗
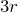
、オームの法則より
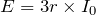
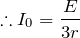
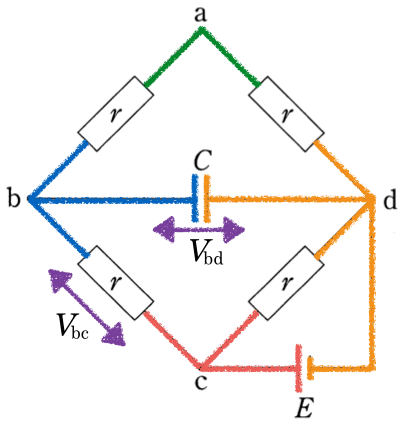
流れている電流は今求めた
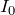
だから、
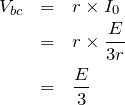
ここまでは順調だね。問題はこの次かな。コンデンサーにかかる電圧
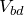
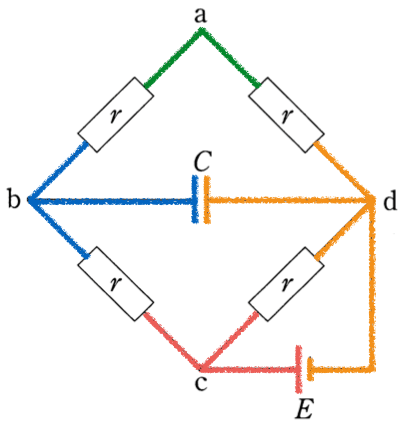
は分かるかな?色分けした線がかなりヒントになっていると思うけど。
たぶん、
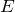
と
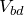
が関係していると思うんだけど、どうなんだろう?
電池は負極よりも正極の方が電位が高いから、cの電位は
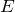
かな?
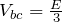
だから、これを足すか、引くかなんだけど、どう考えるの?
そうか!抵抗には、電位の高い方から低い方へ電流が流れるから、cの方が電位が高いのね。ということはbの電位は引き算でいける!
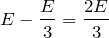
これがbの電位なので、dの電位を0にしたから、コンデンサーにかかる電圧は
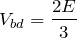
できてるね。それでは、コンデンサーにたくわえられている電荷
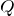
を求めよう!
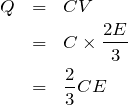
![]() なので、すごく簡単になるんだ。まずは等電位のところを分かりやすくするよ。
なので、すごく簡単になるんだ。まずは等電位のところを分かりやすくするよ。![]() なので、抵抗の配置が左右対称になっているよね。なので、図中に書いた各抵抗の電圧を考えると、
なので、抵抗の配置が左右対称になっているよね。なので、図中に書いた各抵抗の電圧を考えると、![]() 、
、![]() となるんだ。
となるんだ。![]() なので、オームの法則を使ってみよう。
なので、オームの法則を使ってみよう。![]()
![]()
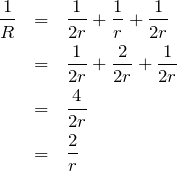
![]()
![]()
![]()
![]() を求めよう。
を求めよう。![]()
![]()
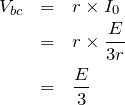
![]() は分かるかな?色分けした線がかなりヒントになっていると思うけど。
は分かるかな?色分けした線がかなりヒントになっていると思うけど。![]()
![]()
![]() を求めよう!
を求めよう!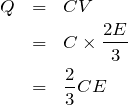
















コメント
[…] 2015年度追試第2問A「直流回路・コンデンサー」 […]