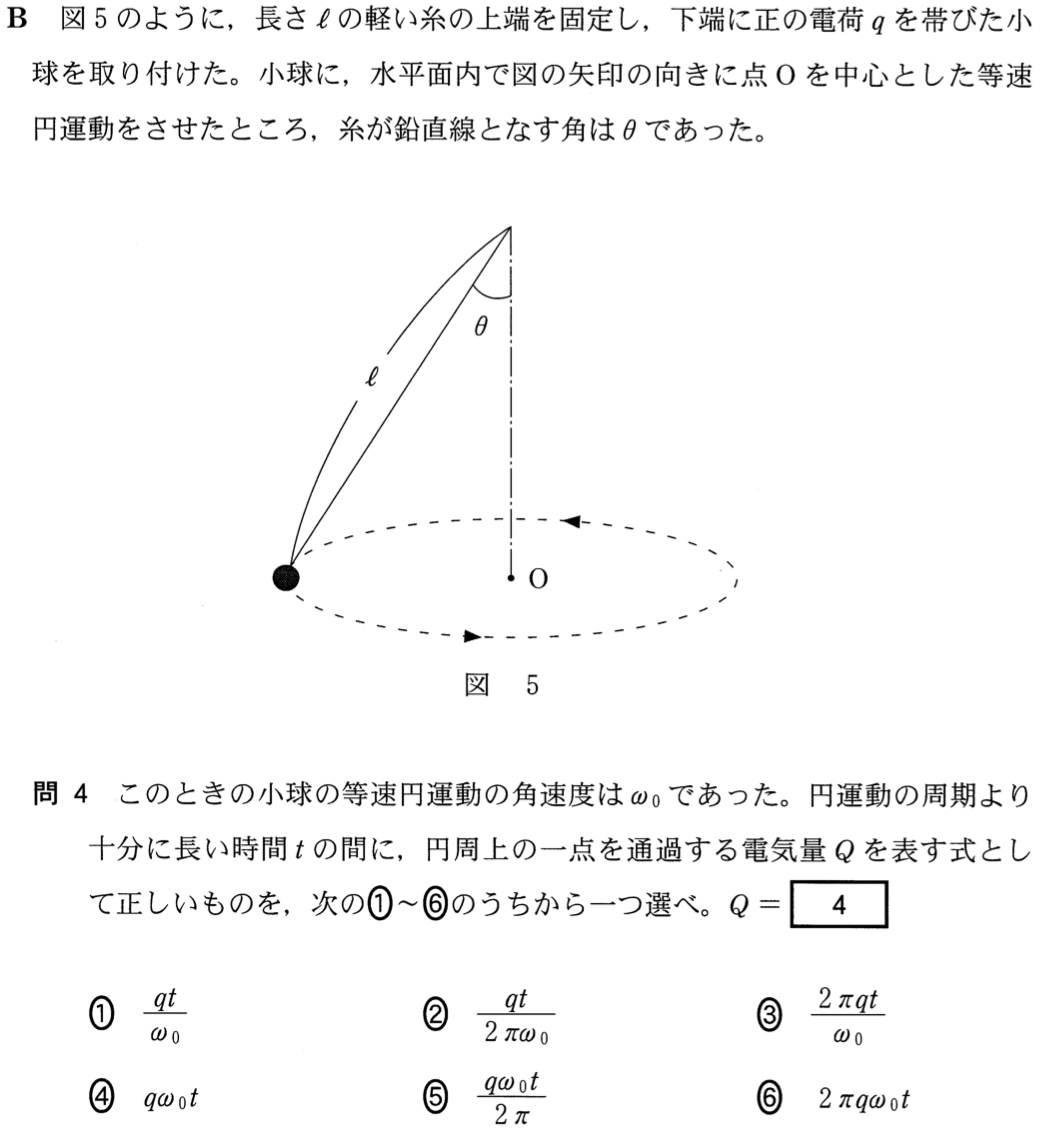
図を見て円錐振り子の問題だ！って思ったけど、問題文に電荷が出てきてよく分からなくなったわ。
あまり気にすることはないよ。基本は円錐振り子だよ。それにちょっと電磁気の話が出てくるっていう感じかな。
ただ、問題が少し分かりにくいの。「時間
の間に、円周上の一点を通過する電気量
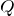
ってどういう意味？
まず「円周上の一点」をどこでもいいんだけど、とりあえず右側の点だと考えてみよう。
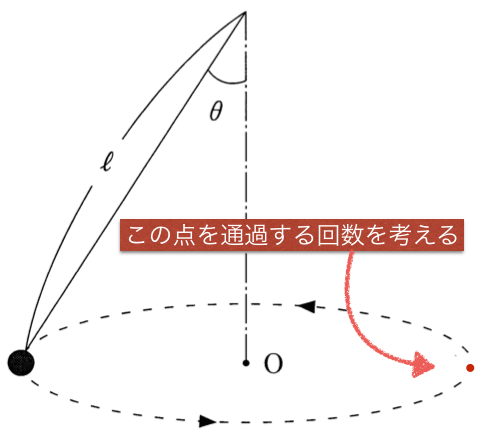
例えば、小球は電荷
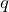
を帯びているので、この点を１回通過すると、この点を通過した電気量はどうなるかな？
１回だったら通過した電気量は
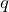
ってことか。じゃあ、２回通過すると
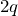
で、ｎ回通過すると
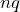
になるのね。
そういうことだね。それじゃあ
、時間の間に何回通過するか計算すればいいね。
１回転で１回と数えればいいのよね。１回転する時間は周期
だから、時間
の間では
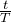
回よね。
そうだね。じゃあ円運動の周期
は覚えてる？
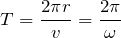
それじゃあ、
を求めてみるわ。
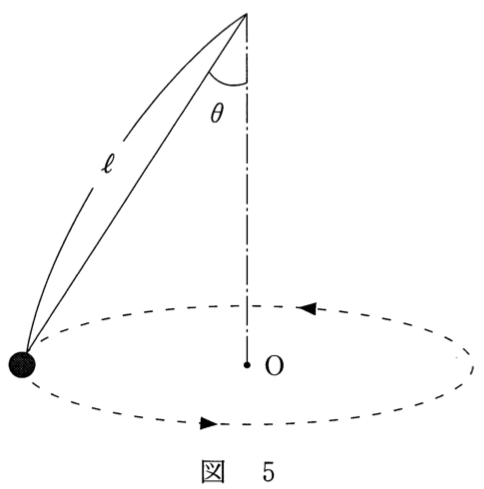
円周を流れる電流が、円の中心に作る磁場ね。教科書に載っているのは導線を流れる電流だったけど、この問いのように電荷が円運動している場合でも、同じように磁場ができるの？
そういうことだよ。問題文に「円周を流れる電流と見なせる」と書かれているので、そう考えていいんだね。
向きは、右ねじの法則に従うんだよね。強さは･･･電流が作る磁場の公式っていろいろあって、なかなか覚えられないのよ。
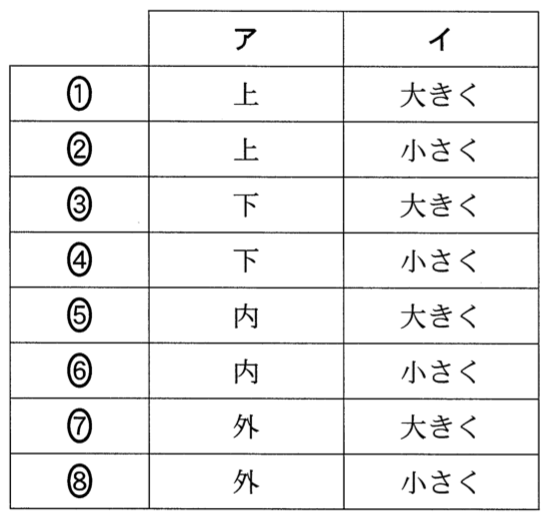
右ねじの法則で考えると、円の中央の磁場の向きは鉛直上向きね。なので①、②、③のどれかね。強さを求めるには、円運動の半径が必要だわ。
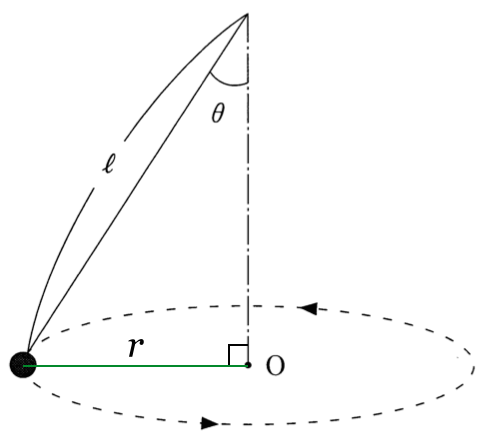
円運動の半径は、
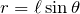
だから、
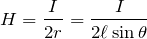
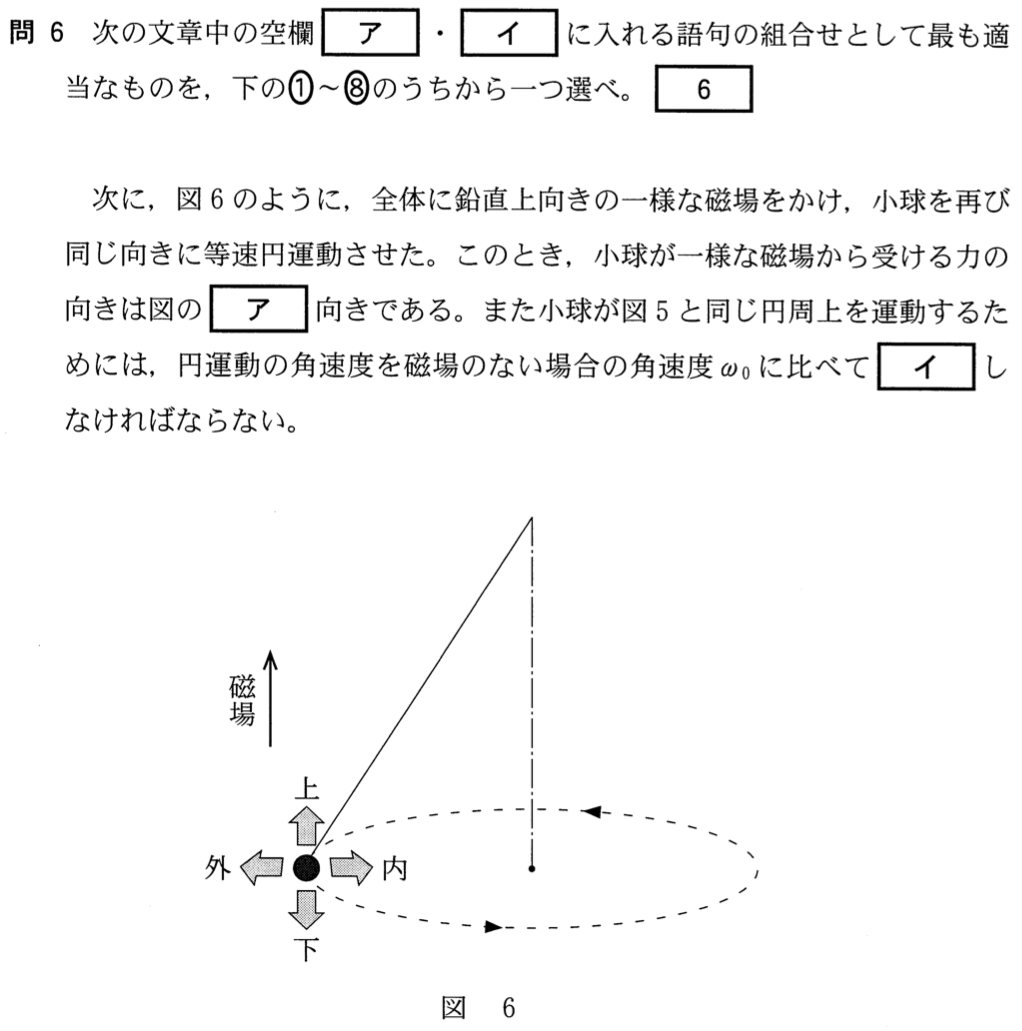
順番に考えれば、そんなに難しくはないんだけどね。磁場の中で電荷が動くときにはたらく力をなんというか知ってる？
えっと、確かフレミング左手の法則に従うんじゃなかったっけ。
そのとおり。フレミング左手の法則を使うときの電流の向きは、動いている電荷の正負によるので、ちゃんと見ておこうね。
問題文の一番最初に正の電荷って書いてあるから、電荷の動く向きがそのまま電流の向きとして考えていいのね。ということは、フレミング左手の法則を使うと・・・はたらく力は外向きね。
そうだね。答えは⑦か⑧に絞られたね。外向きの力が加わったということだから、角速度はどうなればいいと思う？
あんまりよく分からないけど、大きくするか、小さくするかの２択だから、「大きくする」に賭けてみようかな。
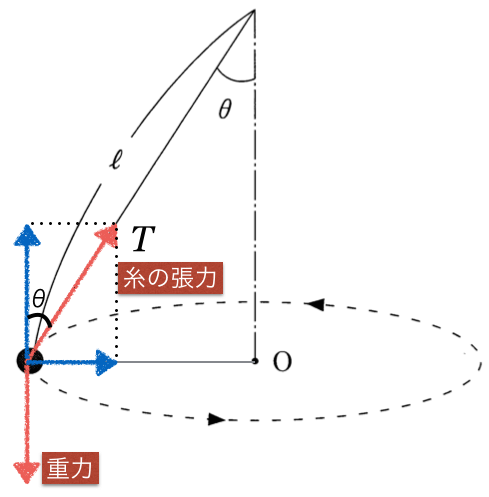
円運動には向心力が必要で、この場合は糸の張力
の水平成分が向心力になっているということね。
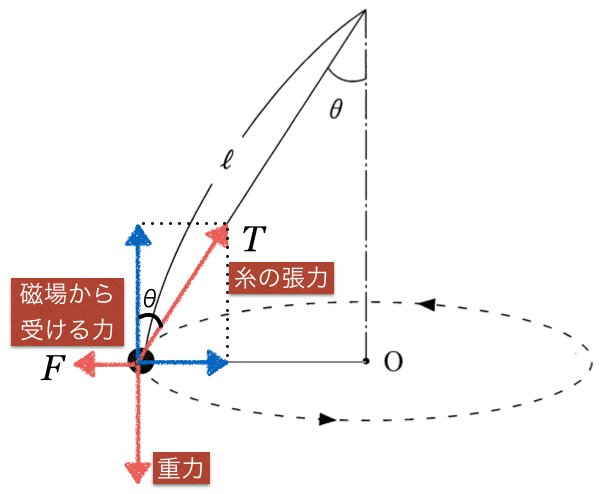
外向きの力が加わったけど、角速度との関係がよく分からないわ。
確かに分かりにくいよね。こういう場合は、運動方程式を立ててみよう。運動方程式は分かる？
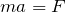
ね。
小球の質量を
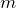
として、円運動の加速度はどうなるか分かる？
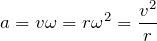
角速度
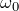
が与えられているから、
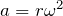
よね。
それじゃあ、磁場を賭ける前と後、それぞれについて運動方程式を立ててみよう。
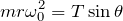
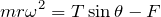
いいね。この２つの式を比較すると、磁場がかかっているときの角速度
は大きくする？小さくする？
磁場がかかっているときの方が右辺が小さいのは明らかだから、左辺も小さくなきゃダメだわ。ということは角速度は小さくしなければならないのね。
