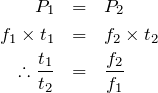ドップラー効果の問題ね。音源が単振動しているのは難しそうね。
ちょっと待って!確かに台はAB間を往復運動しているけど、単振動ではないんだ。
この運動は台が一定の速さで往復運動しているでしょ。常に速さが変化していなきゃ単振動とは言わないんだ。詳しくはこの「
単振動」のページを見てみてね。
ということは、この台の運動は単振動ではなく、ただの往復運動ということね。
問題文にある、「音源が振動する回数」って何?振動数のこと?
そうだよ。例えばスピーカーから振動数が440Hzの音が出ているとすると、
スピーカーのコーンと呼ばれる部分が1秒間に440回振動しているんだ。だからこの問題ではコーンのことを音源と呼んでいることになるね。一般的にはスピーカー全体のことを音源と呼ぶことが多いので、この文章の表現ではスピーカー自体が振動しているように感じるっていう意味で、ちょっと紛らわしい表現かな?正しい表現ではあるんだけどね。
分かったわ。それじゃあ、音源が一定の振動数
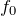
で振動しているっていうことは、1秒間に
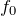
回振動しているっていうことよね。台がAからBまで移動する時間

が分かれば、振動数とかけ算すれば答えがでるっていうことね。
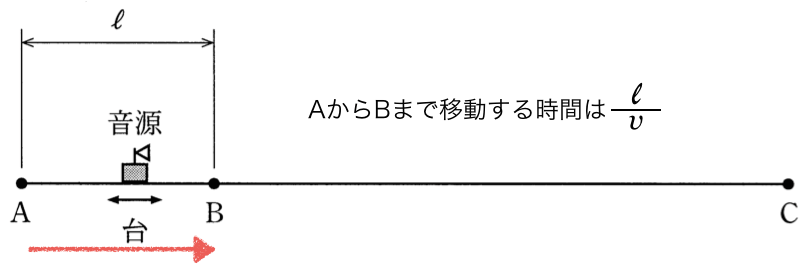
はやさ

で等速運動しているんだから、
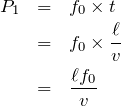

いよいよドップラー効果の問題ね。ドップラー効果の問題で、時間が聞かれる問題が一番苦手!
ドップラー効果の問題って、大きく分けると2種類あって、1つはドップラー効果の公式を使って解く問題。もう1つはドップラー効果の公式を導くような問題なんだ。ところが、この問題はよく読んで考えてみると、その2つのどちらでもないことに気がつくと思うんだけど。
そもそもCで聞こえる音の振動数
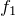
と
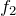
が与えられているでしょ。それと「
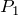
と
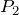
が等しいことから〜」と書いてあるので、当然
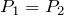
という式を使うでしょ。
ということは、問題文から考えると、
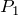
を
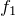
と
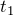
で表せないかな〜と考えるわけね。

そもそも
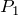
って、台がAからBまで移動しているときに、音源が振動した回数だから、それがそのままCにたどり着いているのよね。
ということは、問1と同じじゃない?振動する回数は振動数
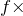
時間

でしょ。ということは、
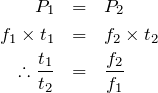
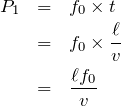
![]() と
と![]() が与えられているでしょ。それと「
が与えられているでしょ。それと「![]() と
と![]() が等しいことから〜」と書いてあるので、当然
が等しいことから〜」と書いてあるので、当然![]() という式を使うでしょ。
という式を使うでしょ。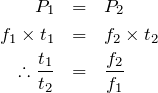
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() と
と![]() が与えられているでしょ。それと「
が与えられているでしょ。それと「![]() と
と![]() が等しいことから〜」と書いてあるので、当然
が等しいことから〜」と書いてあるので、当然![]() という式を使うでしょ。
という式を使うでしょ。