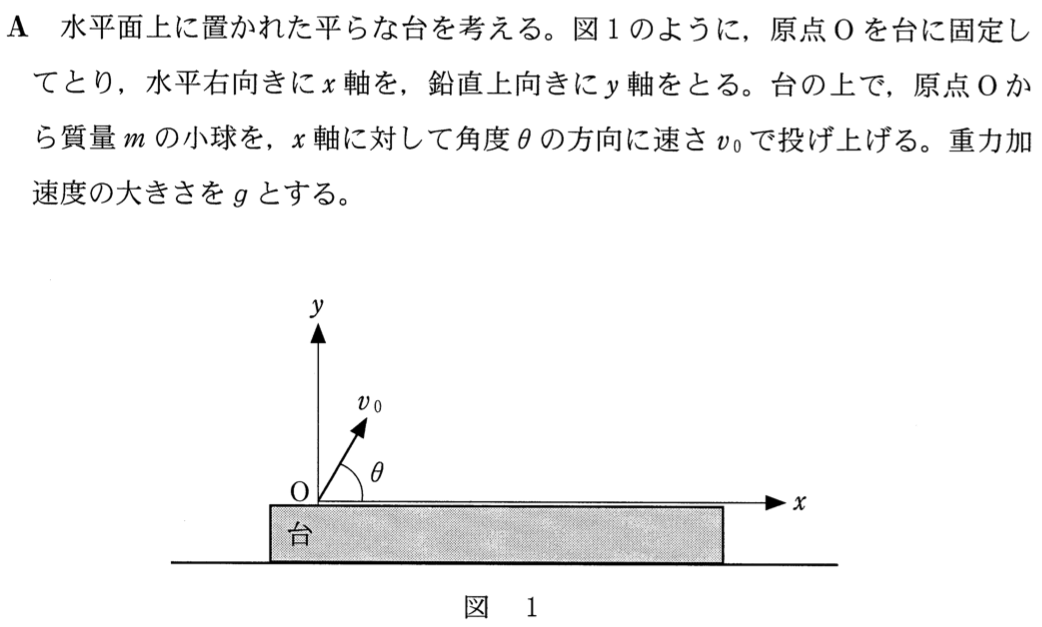

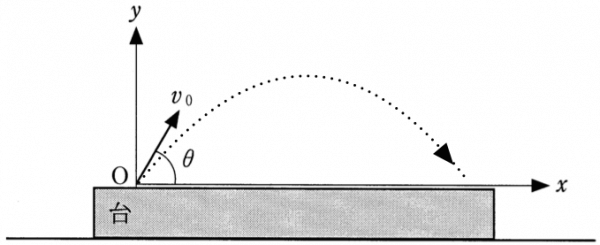
小球の運動は、水平方向と鉛直方向に分けて考えればいいのよね。ここまでは簡単ね。
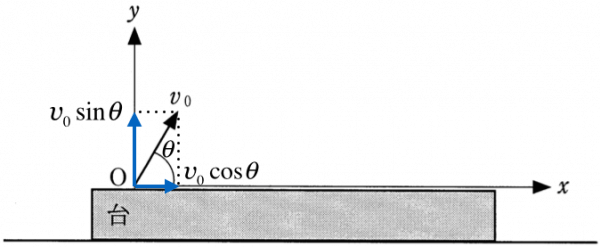
まずは

方向から考えるわ。

方向は等速直線運動だと考えるのよね。

等速直線運動の移動距離は速さ
時間だから、
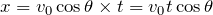
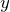
方向は鉛直投射と同じね。上向きが正なので、重力加速度
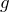
は下向きで考えるのね。
等加速度直線運動の公式
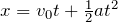
を使って、
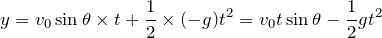

小球と台の運動を別々に考えるよ。まずは台の方が簡単かな。
台の加速度を求めるんだけど、小球を投げ上げたときの台の速さが書いていないから、式が立てられないわ。
そうなんだよね。実は「書いていない」ということは、どんな速さで動いていても、答えは変わらないっていうことなんだ。
ということは、速さが0のときを考えると計算が簡単になるよね。
そうなんだけど、一応今は速さが

として考えてみない?
え〜そうなの。まぁどんな速さでも同じなのか確かめてみるっていうことね。
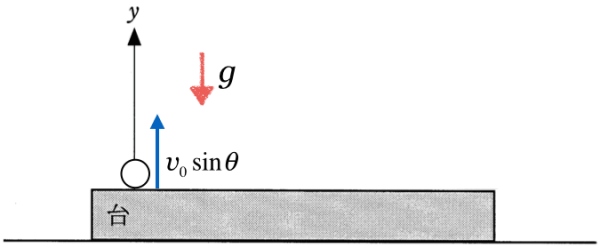
次に小球の運動を考えてみると、まず投げ上げた角度が60°となっているので、代入しちゃうよ。それと、台の速さが

のときに投げ出すので、小球も水平右向きに

だけ速さが速くなるよ。図で表すとこんな感じかな。
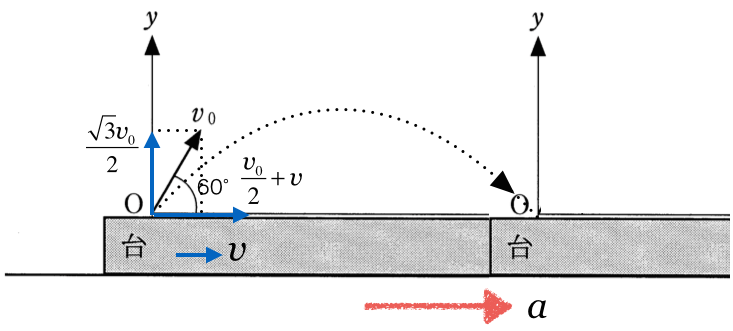
この図ができれば、なんとかなるかな?でも「小球が原点0に戻ってきた」というのを、式で表すにはどうすればいいのかな?
そのあたりがなかなか難しいね。戻ってくる、ということを表すには、どうすればいいかな?
小球が落ちてきたときに、小球の位置と、原点の位置が同じであることかな。
その通り!水平方向だけ考えると、台は等加速度運動で、小球は等速運動なので、台と小球の運動は違うね。だけど、落ちてきたときには同じ位置にあるっていうことだね。
そうよね。でも、落ちてきたときっていうのが、どうなるのかな?
斜方投射で、落ちてくるまでの時間を求めよ、っていう問題をやったことないかな?
そう言われるとやったことあるような気がするけど・・・覚えてないよ。
そうか。落ちてくるまでの時間を

として、鉛直方向だけ考えるんだけど・・・
なるほど。
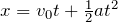
の式を使って、求めるのかな?
鉛直方向だけ考えて、戻ってくるまでの時間だから
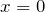
とすればいいのね。
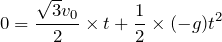
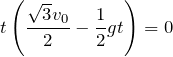
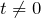
なので、
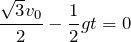
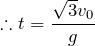
この時間の間に、等加速度で台が動いた距離と、等速度で小球が動いた水平成分の距離が等しいのよね。
台には
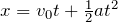
の式を使って、小球の水平成分には距離=速さ
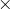
時間を使って、
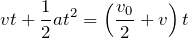
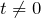
なので、
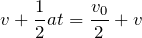
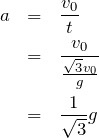
計算が大変だったけどできたね。答えは②だ。結果的に

が消えたでしょ。つまりどんな台がどんな速さでも結果は同じになるということだね。
![]()
![]()
![]() として考えてみない?
として考えてみない?![]() のときに投げ出すので、小球も水平右向きに
のときに投げ出すので、小球も水平右向きに![]() だけ速さが速くなるよ。図で表すとこんな感じかな。
だけ速さが速くなるよ。図で表すとこんな感じかな。![]() として、鉛直方向だけ考えるんだけど・・・
として、鉛直方向だけ考えるんだけど・・・![]()
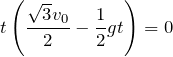
![]()
![]()
![]()
![]()
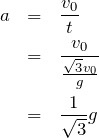
![]() が消えたでしょ。つまりどんな台がどんな速さでも結果は同じになるということだね。
が消えたでしょ。つまりどんな台がどんな速さでも結果は同じになるということだね。 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]()
![]()
![]() として考えてみない?
として考えてみない?![]() のときに投げ出すので、小球も水平右向きに
のときに投げ出すので、小球も水平右向きに![]() だけ速さが速くなるよ。図で表すとこんな感じかな。
だけ速さが速くなるよ。図で表すとこんな感じかな。![]() として、鉛直方向だけ考えるんだけど・・・
として、鉛直方向だけ考えるんだけど・・・![]()
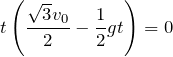
![]()
![]()
![]()
![]()
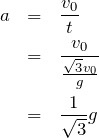
![]() が消えたでしょ。つまりどんな台がどんな速さでも結果は同じになるということだね。
が消えたでしょ。つまりどんな台がどんな速さでも結果は同じになるということだね。