物理が苦手な文子
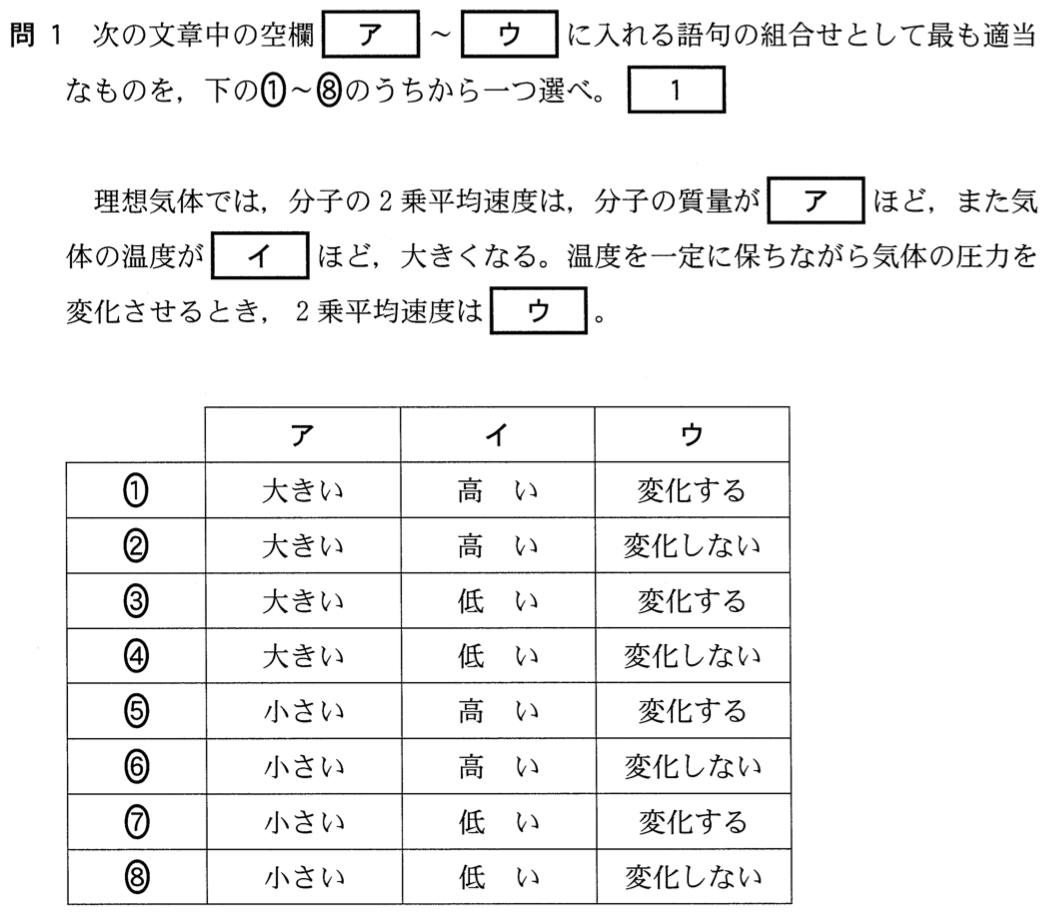
分子の2乗平均速度って、公式みたいのがあるんだっけ?
物理が得意な秀樹
確かに教科書には載ってるね。もちろん、公式を覚えていたらこの問題は簡単なんだけど、覚えていなくても関係性が分かっていれば、答えは出せるんじゃないかな?
物理が苦手な文子
確かに空欄に入るのは、関係性ばかりだもんね。
物理が得意な秀樹
まずは分子の2乗平均速度と分子の質量の関係だね。何か覚えていることはないかな。
物理が苦手な文子
「2乗平均速度は温度で決まる」のか、「運動エネルギーは温度で決まる」のか、どちらかだったと思うんだけど。
物理が得意な秀樹
すごいじゃない!どっちも正解だよ。飛び回っている分子のスピードが速いと,温度が高いって言うことなんだよね。実際に大切なのは,運動ネルギーの方で,こんな感じだよ。

物理が苦手な文子
そういうことなのね。ということは、運動エネルギーは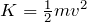 だから,運動エネルギーが一定だとすると,質量が小さい方が速さは速くなるわね。
だから,運動エネルギーが一定だとすると,質量が小さい方が速さは速くなるわね。
物理が得意な秀樹
そうだね。これで⑤〜⑧に絞られたね。2乗平均速度と温度との関係はどうなるかな。
物理が苦手な文子
温度が高いと運動エネルギーは大きいのよね。つまり,2乗平均速度も大きくなるでしょ。
物理が得意な秀樹
まぁそうだね。⑤か⑥だ。教科書には平均の運動エネルギーは絶対温度に比例するという次のような式が書かれているよ。
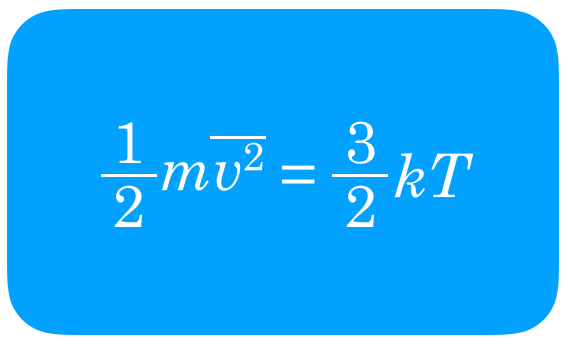
物理が苦手な文子
見たことがあるような気もするわ。この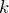 って何?
って何?
物理が得意な秀樹
「ボルツマン定数」っていう名前が付いているよ。簡単に説明すると,「1分子あたりの気体定数」のことなんだけど,とにかく「定数である」っていうことが大切だよ。
物理が苦手な文子
なるほどね。最後は、「温度を一定に保ちながら気体の圧力を変化させる」のね。2乗平均速度は圧力や体積とは関係がないんだから、答えは「変化しない」ね。
物理が得意な秀樹
正解!答えは⑥だ。一応さっきの式を変形するとこうなるよね。

物理が得意な秀樹
ちょっと文字にするとややこしいけど,左辺が2乗平均速度のことで,絶対温度の平方根に比例しているんだね。次は問2だ。
物理が苦手な文子
あれ?計算じゃない!やっぱり公式を覚えていなきゃできないんでしょ。
物理が得意な秀樹
確かにこれも公式を覚えていれば、答えは出せるね。でもなんでもかんでも覚えればなんとかなる、っていうことでもないんだ。
物理が苦手な文子
え、だって計算するのよ。
物理が得意な秀樹
そうだね。でも大丈夫。じゃあ、最初に出てくる「単原子分子理想気体」っていう言葉から何か思い出さない?
物理が苦手な文子
よく聞くキーワードよね。確か、内部エネルギーが決まってるんだよね。
物理が得意な秀樹
そこまで覚えていたら、出てこないかな?
物理が苦手な文子
確か、こんな感じ。
![]()
物理が得意な秀樹
ちゃんと覚えてるね。実は理想気体の場合、その内部エネルギーって、運動エネルギーの総和なんだよね。
物理が苦手な文子
ということは、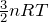 を計算すればいいの?
を計算すればいいの?
物理が得意な秀樹
ただそれは、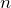 モルの気体の場合の式だよ。この問題は分子1個あたりだから、どうすればいいかな?
モルの気体の場合の式だよ。この問題は分子1個あたりだから、どうすればいいかな?
物理が苦手な文子
1モルあたりにして、さらにアボガドロ定数で割ればいいのね。
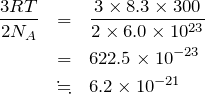
物理が得意な秀樹
ということは、答えは②だね。最後に問3だ。
物理が苦手な文子
定積モル比熱と、定圧モル比熱の関係ね。
物理が得意な秀樹
定積モル比熱を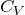 、定圧モル比熱を
、定圧モル比熱を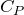 とすると、①は
とすると、①は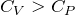 、②は
、②は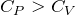 、③は
、③は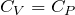 、④は
、④は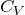 と
と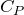 は無関係ということだ。
は無関係ということだ。
物理が苦手な文子
定積モル比熱とか、定圧モル比熱っていう言葉を聞くと、すごく難しく感じるんだけど、この関係は聞いたことあるわ。
物理が得意な秀樹
どんな感じ?
物理が苦手な文子
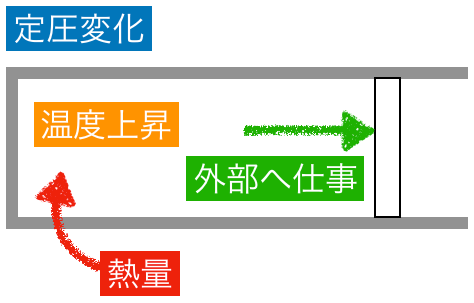
確か、定圧変化だと加えた熱が、温度上昇だけじゃなくて、仕事にも使われるから、比熱が大きくなるんじゃなかったっけ。
物理が得意な秀樹
その通りだよ。確認をしておくよ。モル比熱って,こういうことだよね。

物理が得意な秀樹
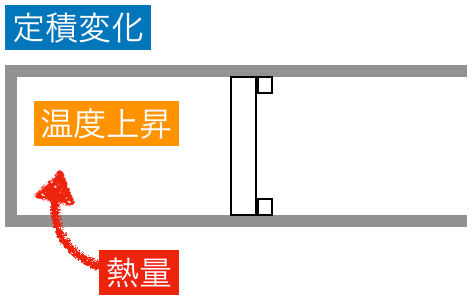
気体の場合は,同じだけ温度を上げるにも,定積変化と定圧変化で必要な熱量が違うんだよね。
物理が苦手な文子
この定積変化の時のモル比熱が「定積モル比熱」で,定圧変化の時が「定圧モル比熱」よね。
物理が得意な秀樹
そうだね。この定積モル比熱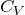 と定圧モル比熱
と定圧モル比熱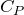 の関係はマイヤーの関係式という式で表せるんだ。
の関係はマイヤーの関係式という式で表せるんだ。

物理が苦手な文子
この式は覚えていなきゃダメなの?
物理が得意な秀樹
覚えていなくてもいいけど,知っていると便利だし,この式を導き出す問題も良く出題されるね。
物理が苦手な文子
そうなのね。
物理が得意な秀樹
ちなみに単原子分子理想気体の場合は,こんな感じ。

物理が苦手な文子
確かに引き算すると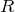 になるわね。
になるわね。
物理が得意な秀樹
そういうわけで,答えは②だね。