
この問題は、よく見るような気がする。ただ熱容量って、比熱とこんがらがるのよね。
そうだね。使われる文字も熱容量が大文字の
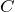
で、比熱が小文字の

で表すから、そのあたりもこんがらがる原因になっているかもね。
そうなのよ。でも
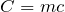
っていう式はなんとなく覚えてるわ。
この問題では使わないけど、大切な式だね。その熱容量と比熱の関係に加えて、熱量と比熱か熱容量の関係が分かれば、大丈夫だね。
確か
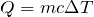
よね。
そうだね。ということはさっきの式と合わせるとどうなる?
そうか。
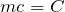
なんだから、
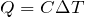
なのね。
そういうことだ。式が立てやすいように図を描いてみるよ。
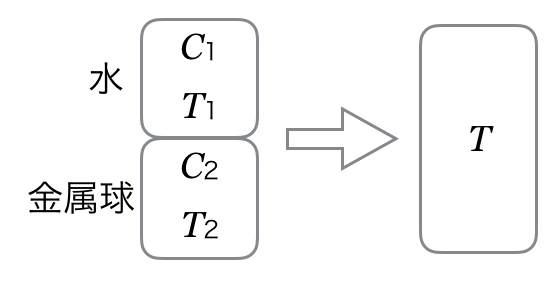
文章だけよりも、こういう図が描けると分かりやすくなるわね。
それじゃあ、問題文にあるけど

なので、しばらく経って等しくなった温度

と
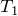
、
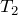
の大小関係はどうなるかな。
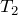
より温度が高くなったり、
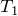
より温度が低くなる可能性はないから、
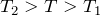
でしょ。
その通り。それでは熱量の保存の関係を使って、式を立ててみよう。
いつもここまでは分かるんだけど、式を立てるときに迷うのよ。でもさっきの図があると分かりやすいわ。
「水が得た熱量=金属球が失った熱量」
なので、
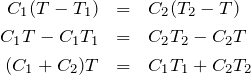
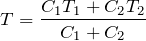
正解!ということは、答えは①か⑤だね。あとはこの変化が、「可逆変化」なのか「不可逆変化」なのかだね。
「可逆変化」、「不可逆変化」ってなんとなく分かるんだけど、正確には分からないわ。ただ、この熱の移動は、「不可逆変化」だと思うけど、どう?
「可逆変化」、「不可逆変化」って、厳密に説明しようとすると難しいんだよね。簡単に説明すると「不可逆変化は放っておいたら絶対に戻らない変化」という感じかな。
放っておいたら、ということは、放っておかなければ戻ることもあるの?
この問題の温度変化も、金属球を加熱して、水を冷やせば元の温度に戻るでしょ。だけど「加熱する」など、エネルギーを加えなければ元に戻らないから、この変化は「不可逆変化」なんだよ。
実際この問題のような熱量の移動は、教科書に「不可逆変化」の例として載っているんだ。というわけで、答えは⑤だね。

![]() で、比熱が小文字の
で、比熱が小文字の![]() で表すから、そのあたりもこんがらがる原因になっているかもね。
で表すから、そのあたりもこんがらがる原因になっているかもね。![]() っていう式はなんとなく覚えてるわ。
っていう式はなんとなく覚えてるわ。![]() よね。
よね。![]() なんだから、
なんだから、![]() なのね。
なのね。
![]() なので、しばらく経って等しくなった温度
なので、しばらく経って等しくなった温度![]() と
と![]() 、
、![]() の大小関係はどうなるかな。
の大小関係はどうなるかな。![]() より温度が高くなったり、
より温度が高くなったり、![]() より温度が低くなる可能性はないから、
より温度が低くなる可能性はないから、![]() でしょ。
でしょ。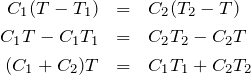
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() で、比熱が小文字の
で、比熱が小文字の![]() で表すから、そのあたりもこんがらがる原因になっているかもね。
で表すから、そのあたりもこんがらがる原因になっているかもね。![]() っていう式はなんとなく覚えてるわ。
っていう式はなんとなく覚えてるわ。![]() よね。
よね。![]() なんだから、
なんだから、![]() なのね。
なのね。
![]() なので、しばらく経って等しくなった温度
なので、しばらく経って等しくなった温度![]() と
と![]() 、
、![]() の大小関係はどうなるかな。
の大小関係はどうなるかな。![]() より温度が高くなったり、
より温度が高くなったり、![]() より温度が低くなる可能性はないから、
より温度が低くなる可能性はないから、![]() でしょ。
でしょ。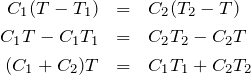
![]()