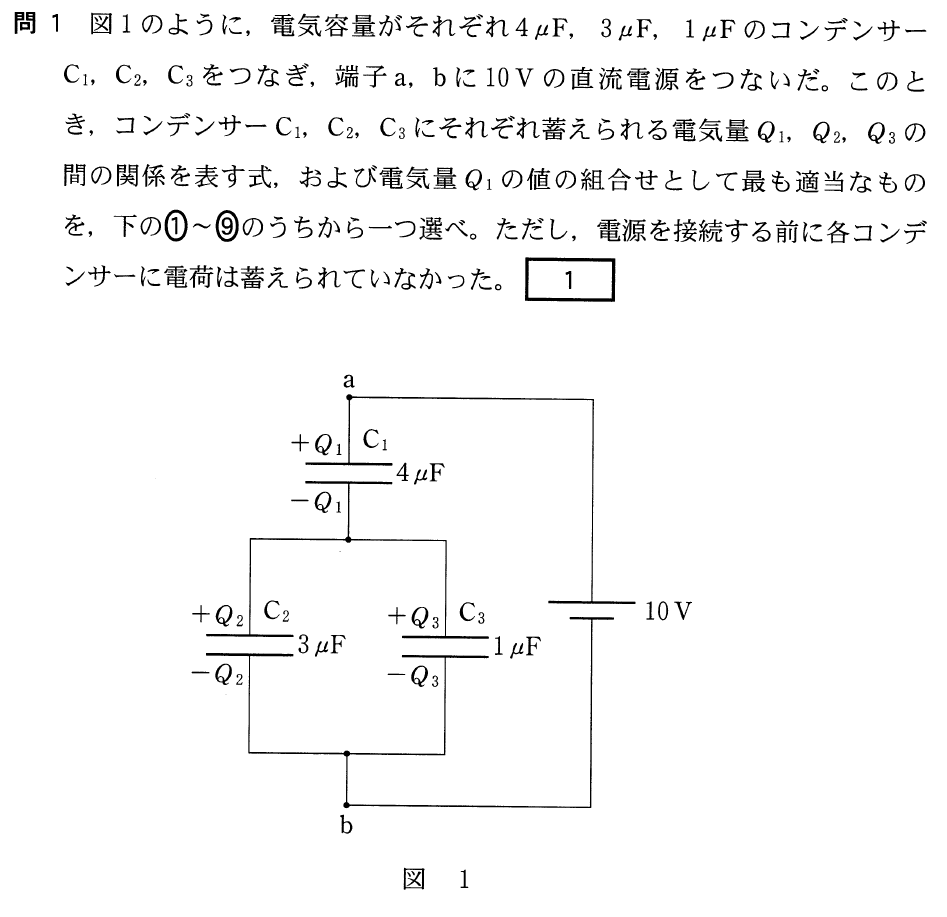
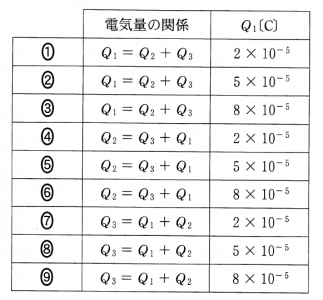
コンデンサーの問題って、使う式は決まっているんだけど、なんか苦手なのよね。
確かにこの問題も、
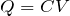
という公式だけで解けるね。ただ文字数が多いので、結構な数の連立方程式になっちゃうかな。
まぁでも地道に計算すればいつかは答えが出るじゃない。この問題もいくつかやり方があって、上手いやり方に気がつくと、未知数が減って、連立する方程式も減るんだよね。
でもね。気がつくかどうかは分からないじゃない。計算さえすれば確実に解ける、っていう方がいいんじゃない?時間も「良い方法がないかな~」って考える時間があるなら、ちょっと計算量が多いかもしれないけど、確実に解ける方法で計算を始めた方が結果的には早く解けちゃったりするんだよ。
確かにね~。じゃあ、「確実に解ける方法」ってどういう方法なの?
さっきでてきた
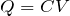
を各コンデンサーに使うんだよ。各コンデンサーの
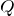
と
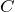
は与えられているから、まず

を決めようか。
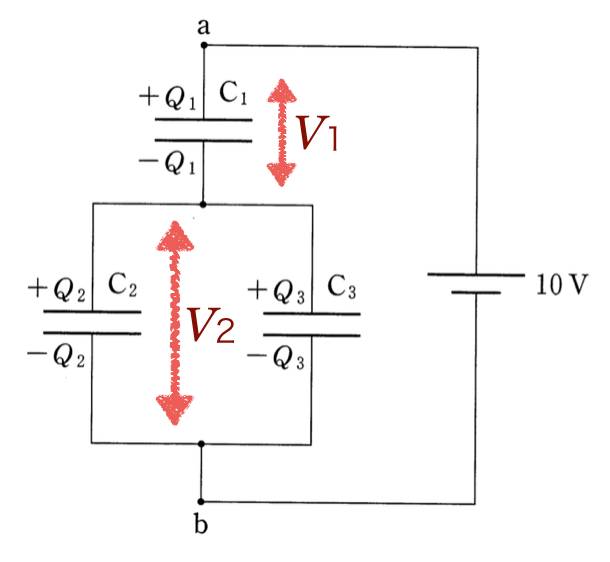
C

とC

は並列なので、同じ電圧ね。なので、図のように決めましょう。
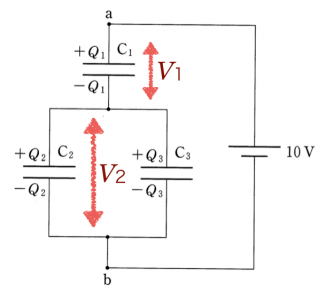
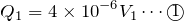
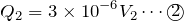
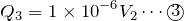
未知数が5つあるから、まだあと式が2本必要ね。電源の電圧10Vは使えない?
そうね。
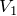
と
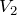
は直列につながっているから、
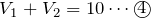
実はこの問題の問1が残りの式を求めているんだね。
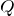
の間の関係だね。赤い線で囲った部分は孤立していて、その中だけで電気が移動しているので、電気量が保存されるっていう式を立てればいいね。
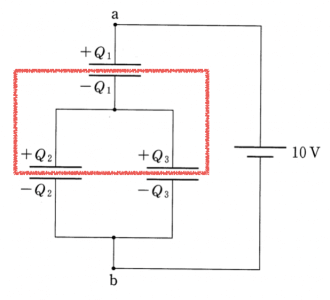
最初はすべてのコンデンサーの電気量は0だったのよね。電源を接続したら、コンデンサーにそれぞれ電気がたまったので、
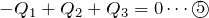
あとは5本の連立方程式を解くのね。④を①に代入して
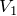
を消去して、①~③を⑤に代入すればいいかな。
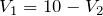
なので、
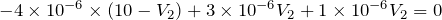
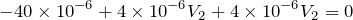
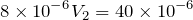
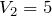
さぁ、あとちょっとだ。求めたいのは
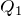
だよ。
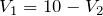
に代入すると、
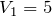
になるので、①に代入すると、
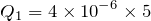
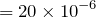
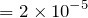


![]() という公式だけで解けるね。ただ文字数が多いので、結構な数の連立方程式になっちゃうかな。
という公式だけで解けるね。ただ文字数が多いので、結構な数の連立方程式になっちゃうかな。![]() を各コンデンサーに使うんだよ。各コンデンサーの
を各コンデンサーに使うんだよ。各コンデンサーの![]() と
と![]() は与えられているから、まず
は与えられているから、まず![]() を決めようか。
を決めようか。![]() とC
とC![]() は並列なので、同じ電圧ね。なので、図のように決めましょう。
は並列なので、同じ電圧ね。なので、図のように決めましょう。
![]()
![]()
![]()
![]() と
と![]() は直列につながっているから、
は直列につながっているから、![]()
![]() の間の関係だね。赤い線で囲った部分は孤立していて、その中だけで電気が移動しているので、電気量が保存されるっていう式を立てればいいね。
の間の関係だね。赤い線で囲った部分は孤立していて、その中だけで電気が移動しているので、電気量が保存されるっていう式を立てればいいね。
![]()
![]() を消去して、①~③を⑤に代入すればいいかな。
を消去して、①~③を⑤に代入すればいいかな。![]() なので、
なので、![]()
![]()
![]()
![]()
![]() だよ。
だよ。![]() に代入すると、
に代入すると、![]() になるので、①に代入すると、
になるので、①に代入すると、![]()
![]()
![]()


コメント
[…] 2016年度第2問A問1「コンデンサー回路」 […]