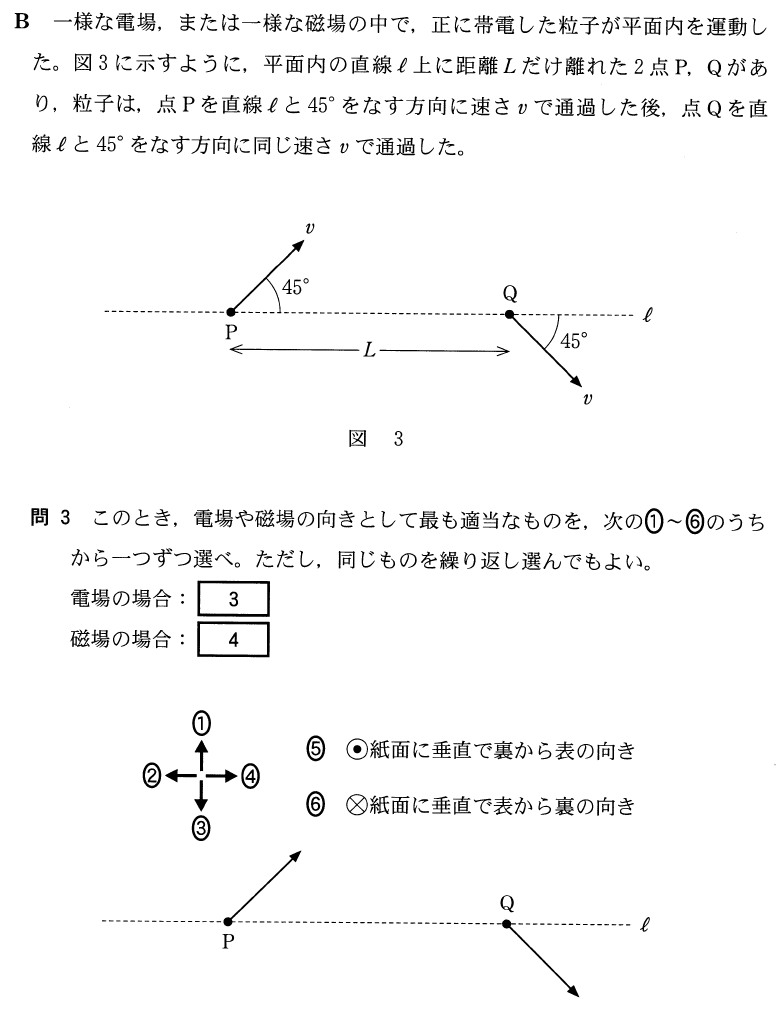
この問題は状況を理解するのに、少し時間がかかるかも。
電場がかかっている場合と、磁場がかかっている場合で、別々に考えるのね。
そういうことだね。まずは電場がかかっているとして考えてみよう。一般に正の電荷は、電場の中でどんな力を受けるかな?
電場と同じ向きに、
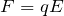
の大きさの力がはたらくのよね。
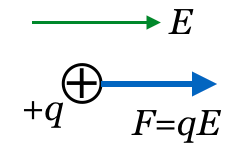
そうだね。常に同じ向きで同じ大きさの力を受けると、物体はどう動くかな?
まぁそうだね。力の向きと運動の向きが同じならだんだん加速するね。力の向きと運動の向きが違ったらどうだろう?
例えば力学の分野で考えると、重力って常に鉛直下向きで
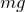
という大きさの力がはたらくよね。重力に対して斜めに動いていたら、その物体はどう動くかな?
あぁ、斜方投射ね。だとすると放物運動するわ。ということは、この粒子も放物運動をするっていうことね。
そうだね。問題の図の点P、点Qが放物運動の途中だとすると、力は向きはどっちかな?
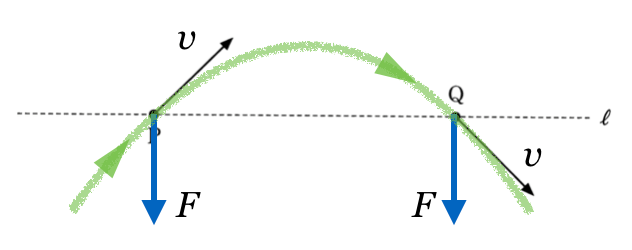
斜方投射と同じと考えると、下向きね。ということは、電場の向きと力の向きは同じだから、電場の向きは下向きね。答えは③。
そうだね。じゃあ、同じように磁場の場合も考えてみよう。一般に正の電荷は、磁場の中でどんな力を受けるかな?
悩むよね。実は電荷が静止している場合は、力を受けることはないんだ。だけど、動いていたら力を受けるんだね。
あーそうか。フレミング左手の法則を使って向きを求めるやつね。
大きさはローレンツ力っていうやつね。
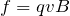
ね。つまり速度

で動いていれば力を受けるけど、

が0なら力も0なのね。
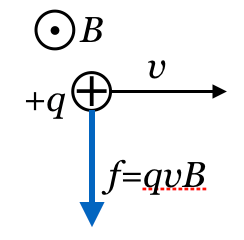
この問題で大切なのは、

の向きと
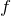
の向きは必ず垂直になるということだ。
ということは、立体的に考えるといろんな向きが考えられるけど、PからQに動いたことを考慮すると、力の向きはこんな感じかな?
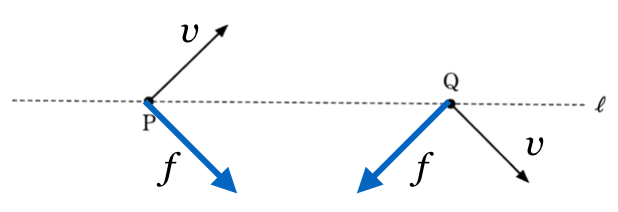
すばらしい!その通りだ。ということは、荷電粒子はどんな運動をすることになるかな?
力の向きがこう変わる運動で知ってるのは、円運動くらいかな。
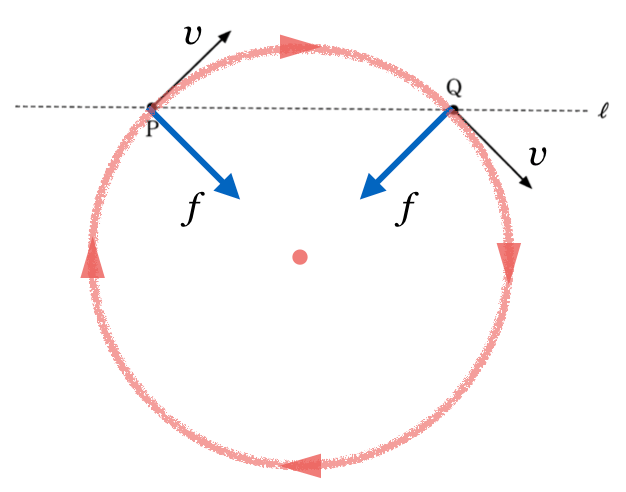
そういえば、磁場の中で荷電粒子は円運動するって聞いたことがあるわ。
フレミング左手の法則で向きを考えるのね。あれ?中指を電流の向きに合わせるんだけど、この場合って電流は流れてないよね。
荷電粒子の運動の場合は、正の電荷なら運動の向きがそのまま電流の向き、負の電荷なら運動の向きの逆が電流の向きだと考えるんだよ。
ということは、左手の中指は電荷の運動の向き、親指を力の向きにすると、人差し指は・・・紙面の裏から表の向きね。答えは⑤ね。
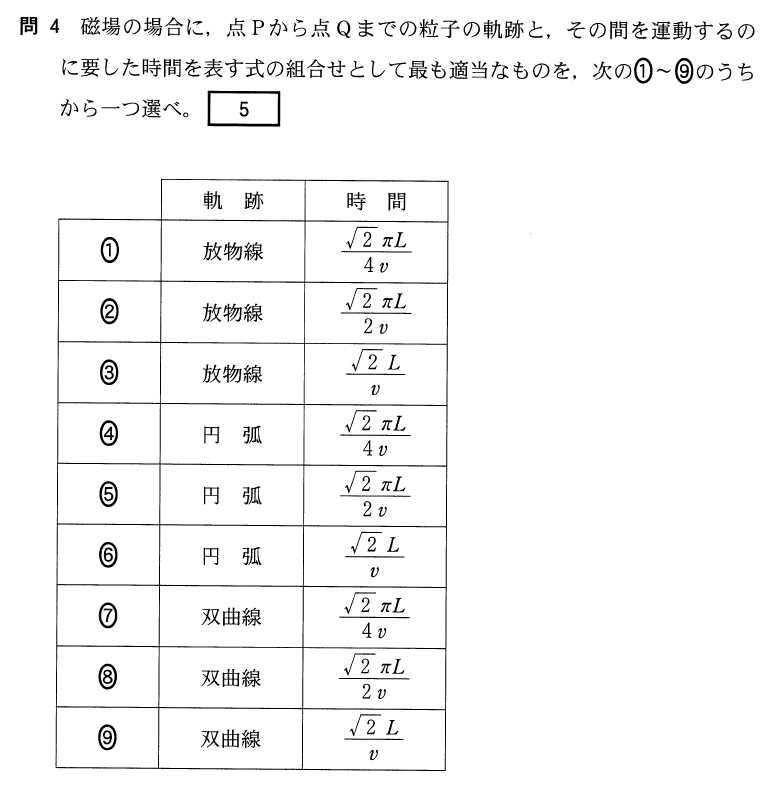
さて、問4の軌跡についてはいいよね。さっきの図でも分かる通り、円運動の一部だから「円弧」を選べばいいね。
円運動の中心と、点P、点Qの関係が分かればできるんだけど、図が描けるかな。
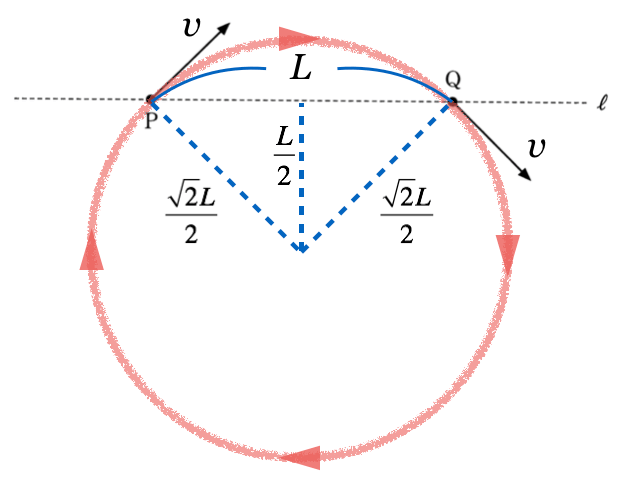
点Pと点Qの

は90°傾いているから、円の中心と作る角も90°になるでしょ。ということは、直角二等辺三角形ができるので、
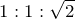
を使うと図のようになるわ。
そうだね。それじゃあ、点Pから点Qまで移動する時間はどうなるかな?
円運動の周期で考えるのかな?中心角が90°だから、1周期の
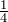
の時間ね。
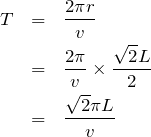
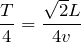

![]() の大きさの力がはたらくのよね。
の大きさの力がはたらくのよね。
![]() という大きさの力がはたらくよね。重力に対して斜めに動いていたら、その物体はどう動くかな?
という大きさの力がはたらくよね。重力に対して斜めに動いていたら、その物体はどう動くかな?
![]() ね。つまり速度
ね。つまり速度![]() で動いていれば力を受けるけど、
で動いていれば力を受けるけど、![]() が0なら力も0なのね。
が0なら力も0なのね。
![]() の向きと
の向きと![]() の向きは必ず垂直になるということだ。
の向きは必ず垂直になるということだ。



![]() は90°傾いているから、円の中心と作る角も90°になるでしょ。ということは、直角二等辺三角形ができるので、
は90°傾いているから、円の中心と作る角も90°になるでしょ。ということは、直角二等辺三角形ができるので、![]() を使うと図のようになるわ。
を使うと図のようになるわ。![]() の時間ね。
の時間ね。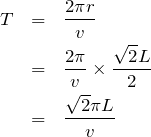
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() の大きさの力がはたらくのよね。
の大きさの力がはたらくのよね。
![]() という大きさの力がはたらくよね。重力に対して斜めに動いていたら、その物体はどう動くかな?
という大きさの力がはたらくよね。重力に対して斜めに動いていたら、その物体はどう動くかな?
![]() ね。つまり速度
ね。つまり速度![]() で動いていれば力を受けるけど、
で動いていれば力を受けるけど、![]() が0なら力も0なのね。
が0なら力も0なのね。
![]() の向きと
の向きと![]() の向きは必ず垂直になるということだ。
の向きは必ず垂直になるということだ。



![]() は90°傾いているから、円の中心と作る角も90°になるでしょ。ということは、直角二等辺三角形ができるので、
は90°傾いているから、円の中心と作る角も90°になるでしょ。ということは、直角二等辺三角形ができるので、![]() を使うと図のようになるわ。
を使うと図のようになるわ。![]() の時間ね。
の時間ね。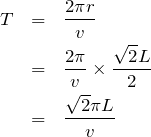
![]()
コメント
[…] 2016年度第2問B「電場・磁場と荷電粒子の運動」 […]