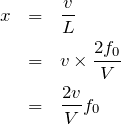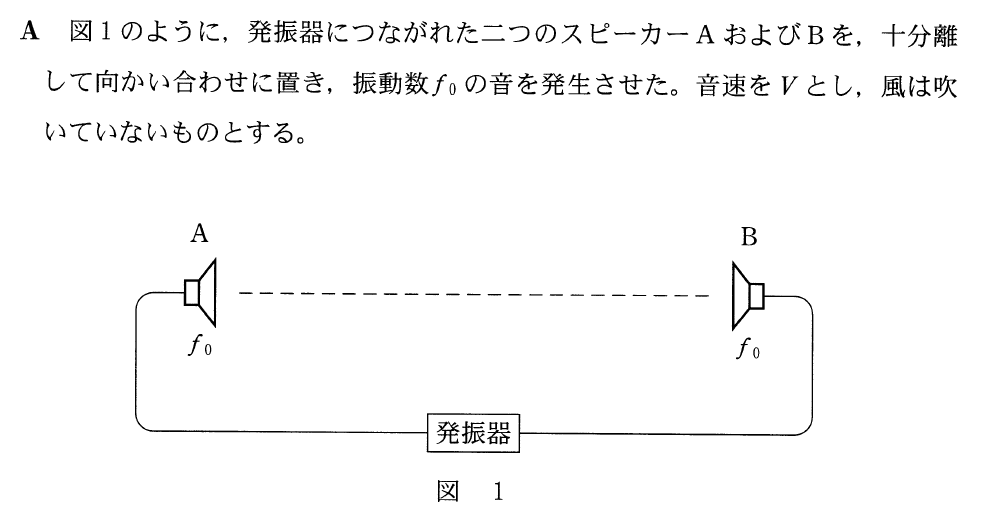
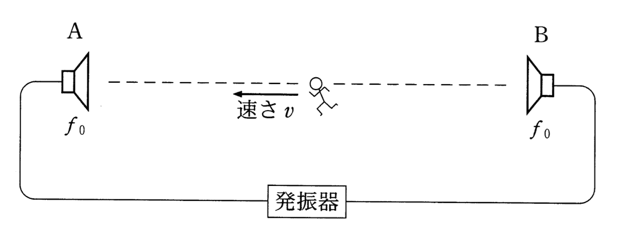
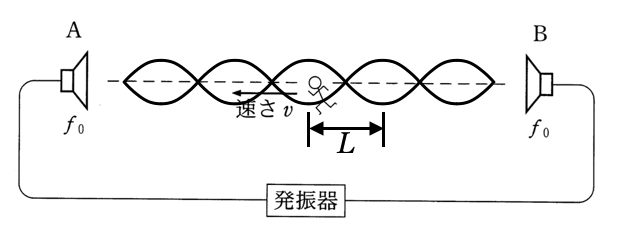
左右から音が出ているんだね。2つのスピーカーの間ではどんなことが起こっているか分かるかな?
音は波なので、一般に波が左右から来てぶつかった状況を考えればいいのね。
確か2つの同じ波がぶつかると、大きく振動する腹と振動しない節ができるんじゃなかったっけ。定常波って言うんだよね。
その通り!じゃあ、この2つのスピーカの間の定常波はどんな風になっているか、描けるかな。本当は音は縦波だけど、横波のように描いてみるんだったよね。
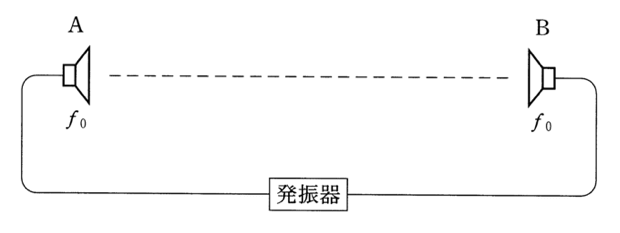
波長や振幅は分からないのでだいたいで描いてくれれば良いんだけど、外せないポイントが1つだけあるんだ。
AとBの中点がどうなっているのか分かるっていうことね。Aのスピーカーからの距離と、Bのスピーカーからの距離が等しいのよね。そうか、波源から等距離ということは、強め合って腹になるのかな?
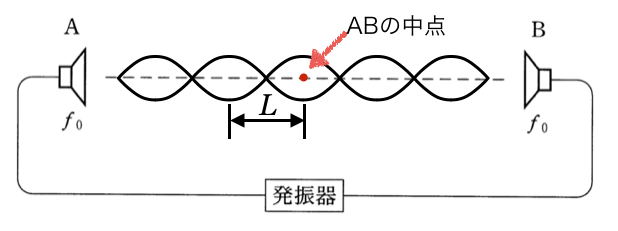
正解だ!この問題ではAとBの中点が腹になる、ということしか分からないから、それさえ守って図を描けば良いんだ。
ABの中点を腹にして定常波を描くと、こんな感じね。腹のところは音がもっとも強めあう点だから、
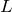
は腹と腹の間隔ね。
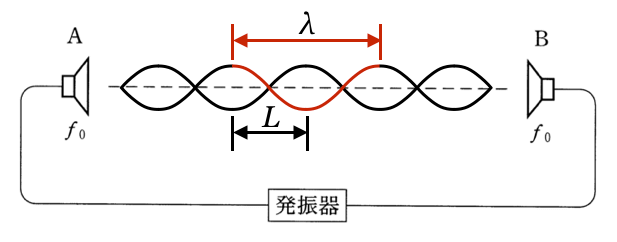
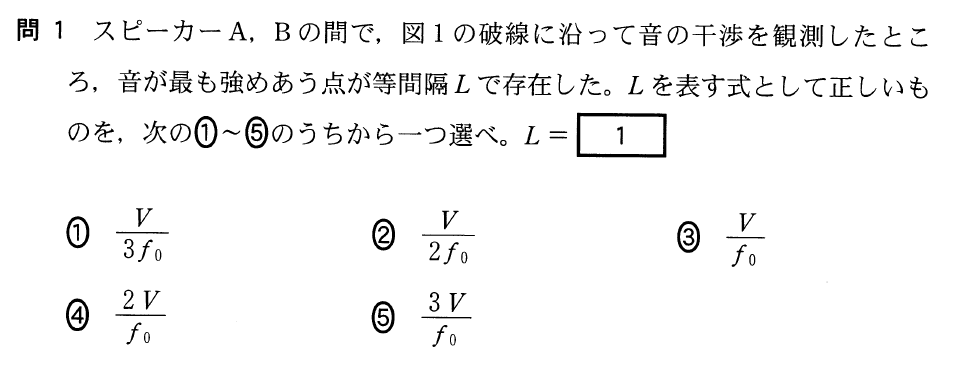
そうだね。それでは問題に戻って、
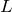
はどう表せるかな。
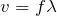
を使うと、
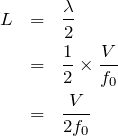
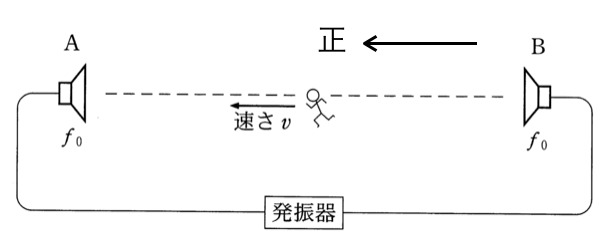
正解!じゃあ、問2へ行こう。この問題は観測者が動いていて、振動数を求める問題だから、ドップラー効果を考えるのは分かるかな?
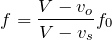
複雑な式だけど、なんとなくこの式は覚えちゃったわ。
この式を覚えていれば、あとはこの問題の設定を入れるだけだね。
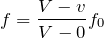
あれ?これでいいのかな?符号が分からなくなっちゃった。
ドップラー効果の公式を使うときには、大切なことが1つあるんだな。覚えてないかな。
そういば、何かあったような・・・そうだ!正の向きね。
そう。ドップラー効果の公式を使うときには正の向きが決まっていて、必ず音源から観測者の向きを正とするんだよ。
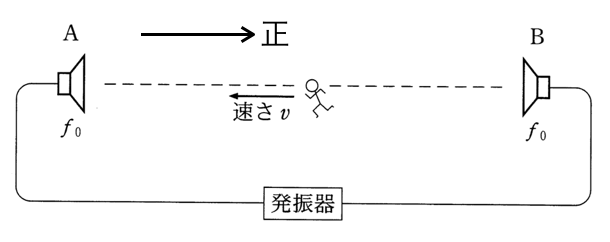
そういえば、そうだった。ということは、観測者はAに向かって動いているから、負の向きということね。なので、
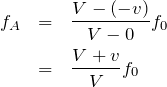
そうだね。じゃあ、次は単位時間あたりのうなりの回数だ。
単位時間あたりのうなりの回数って
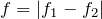
よね。
そうだね。ということは、Aからの振動数を求めた方法と同様に、Bからの振動数を求めて、差をとればいいということだ。やってみて。
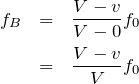
振動数は近づく向きの方が大きくなるので、
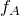
の方が大きいわね。ということは絶対値を外すことができて、
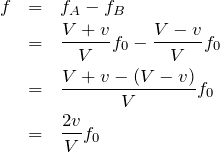
この問題の最後に「このうなりは、音が強め合う場所と弱め合う場所を、交互に観測者が通過することにより聞こえると考えることもできる。」と書いてあるね。
そもそもAB間には定常波ができていて、腹と節があるんだよね。この中を走ると、腹と節を交互に横切るから、観測者には音が強くなったり、弱くなったり聞こえるでしょ。
そうなんだ。例えば腹-節-腹と進むと、1回うなりが聞こえるんだね。
ということは、
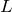
進むごとに1回うなりが聞こえるということだから、1秒間に何回聞こえるかというと、どう計算すればいいのかな?
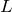
進むのにかかる時間は、
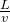
秒なので、時間と回数の比を書くと、
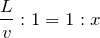
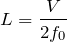
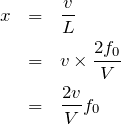
というわけで、ドップラー効果とうなりの関係で求めた答えと同じになるね。




![]() は腹と腹の間隔ね。
は腹と腹の間隔ね。
![]() はどう表せるかな。
はどう表せるかな。![]() を使うと、
を使うと、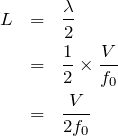

![]()
![]()

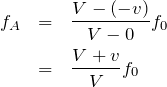
![]() よね。
よね。
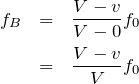
![]() の方が大きいわね。ということは絶対値を外すことができて、
の方が大きいわね。ということは絶対値を外すことができて、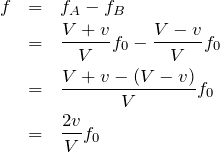

![]() 進むごとに1回うなりが聞こえるということだから、1秒間に何回聞こえるかというと、どう計算すればいいのかな?
進むごとに1回うなりが聞こえるということだから、1秒間に何回聞こえるかというと、どう計算すればいいのかな?![]() 進むのにかかる時間は、
進むのにかかる時間は、![]() 秒なので、時間と回数の比を書くと、
秒なので、時間と回数の比を書くと、![]()
![]()
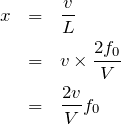
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!



![]() は腹と腹の間隔ね。
は腹と腹の間隔ね。
![]() はどう表せるかな。
はどう表せるかな。![]() を使うと、
を使うと、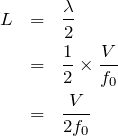

![]()
![]()

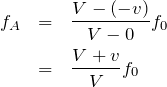
![]() よね。
よね。
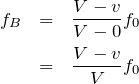
![]() の方が大きいわね。ということは絶対値を外すことができて、
の方が大きいわね。ということは絶対値を外すことができて、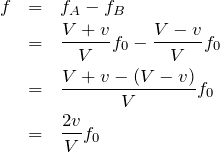

![]() 進むごとに1回うなりが聞こえるということだから、1秒間に何回聞こえるかというと、どう計算すればいいのかな?
進むごとに1回うなりが聞こえるということだから、1秒間に何回聞こえるかというと、どう計算すればいいのかな?![]() 進むのにかかる時間は、
進むのにかかる時間は、![]() 秒なので、時間と回数の比を書くと、
秒なので、時間と回数の比を書くと、![]()
![]()