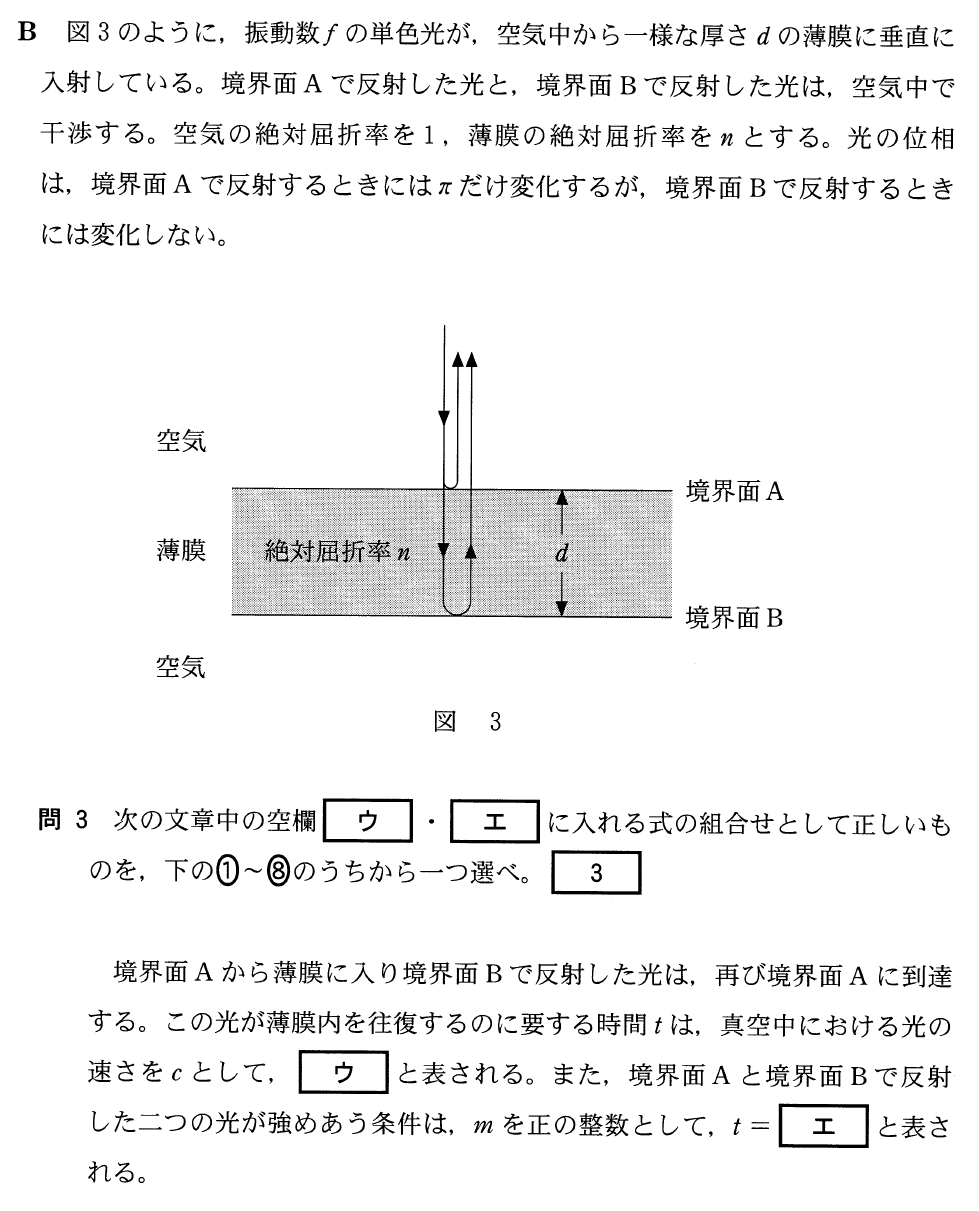
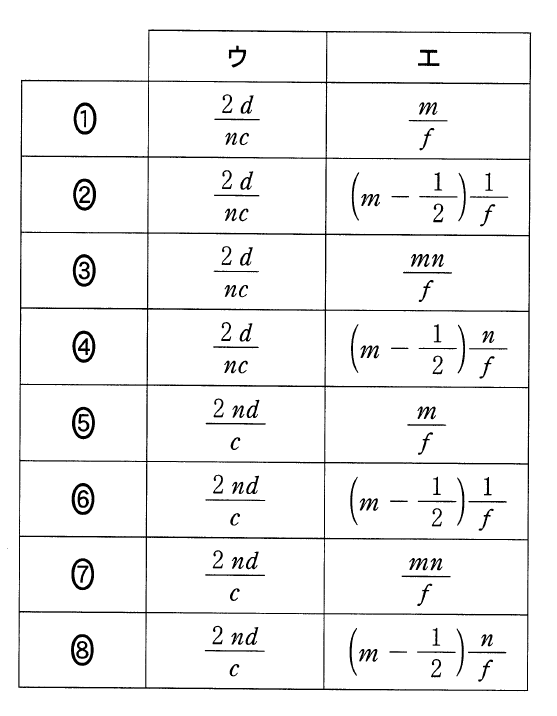
薄膜干渉の問題ね。よく見る問題かな~と思ったら、聞かれているのはあまり見たことがない内容だわ。
そうだね。時間の関係がたくさん聞かれているね。まぁでも考え方は基本通りなのでやってみよう。まず、光が屈折率
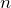
の媒質に入ると、何が変化するか分かるかな?
えっと、波長と速さが
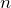
分の1になるのよね。
その通り!この関係は屈折の法則から求められるんだけど、覚えておいた方がいいかもね。あと、振動数は?
分かってるね。それじゃあ簡単だ。まず最初の空欄はどうなる?
これは時間を求めるから、距離÷速さで出せるわ。距離は往復だから
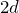
、速さは
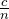
なので、

そうだね。僕もないよ。なので、とりあえず普通に強め合う条件を求めてみようか。
じゃあ、経路差は
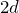
、境界Aだけで位相が反転するので、強め合う条件は・・・
そうだった。波長は
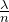
となるのね。
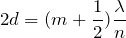
おしい!選択肢を見るとかっこの中が
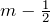
になってるでしょ。
そうか、普段やっていた問題は
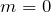
から始まっていたけど、この問題は正の整数だから
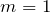
から始まっているっていうことね。
あとは最初の空欄の答えと合わせて
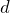
を消去すればいいかな。
ということは、
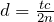
より
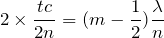
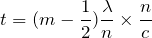
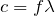
より
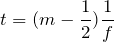
薄膜の厚さが光の波長より十分に薄いときって、どういうこと?
を考えると、強め合う最小の厚さがあるっていうことだね。
だけどまだ膜は薄くすることができるので、さらに薄くなるとだんだんと弱め合っていくということになるね。
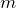
が正の整数であることを考慮すると、弱め合う条件は
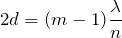
ということになるね。
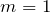
のとき、
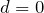
だよね。これって、薄膜が存在するためには
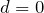
になることはないんだけど、
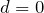
に近づくにつれてどんどん弱め合うっていうことなんだ。
問題に戻ると、まず十分に薄いときは弱め合う。そこから厚くしていくと今度は強め合う。さらに厚くしていくと再び弱め合う。このときの膜の厚さが
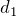
なんだね。ということは、
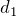
のとき、
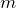
はいくつかな?
最も薄いときが
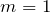
なんだから、次は
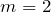
ね。弱め合うときの式に入れると、
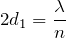
そうだね。ということは、
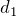
が最も小さいのは、何色の時?
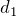
は
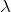
に比例するので、波長が短い青色の時ね。
そうだね。波長の短い順に並べると青、緑、赤だよね。というわけで、答えは③だ。


![]() の媒質に入ると、何が変化するか分かるかな?
の媒質に入ると、何が変化するか分かるかな?![]() 分の1になるのよね。
分の1になるのよね。![]() 、速さは
、速さは![]() なので、
なので、 ![]()
![]() 、境界Aだけで位相が反転するので、強め合う条件は・・・
、境界Aだけで位相が反転するので、強め合う条件は・・・![]() となるのね。
となるのね。![]()
![]() になってるでしょ。
になってるでしょ。![]() から始まっていたけど、この問題は正の整数だから
から始まっていたけど、この問題は正の整数だから![]() から始まっているっていうことね。
から始まっているっていうことね。![]() を消去すればいいかな。
を消去すればいいかな。![]() より
より![]()
![]()
![]() より
より![]()

![]()
![]() が正の整数であることを考慮すると、弱め合う条件は
が正の整数であることを考慮すると、弱め合う条件は![]()
![]() のとき、
のとき、![]() だよね。これって、薄膜が存在するためには
だよね。これって、薄膜が存在するためには![]() になることはないんだけど、
になることはないんだけど、![]() に近づくにつれてどんどん弱め合うっていうことなんだ。
に近づくにつれてどんどん弱め合うっていうことなんだ。 ![]() なんだね。ということは、
なんだね。ということは、![]() のとき、
のとき、![]() はいくつかな?
はいくつかな?![]() なんだから、次は
なんだから、次は![]() ね。弱め合うときの式に入れると、
ね。弱め合うときの式に入れると、![]()
![]() が最も小さいのは、何色の時?
が最も小さいのは、何色の時?![]() は
は![]() に比例するので、波長が短い青色の時ね。
に比例するので、波長が短い青色の時ね。