![]() よね。えーと、気体の温度
よね。えーと、気体の温度![]() が分からないわ。気体定数
が分からないわ。気体定数![]() も与えられていないし。
も与えられていないし。
![]() や
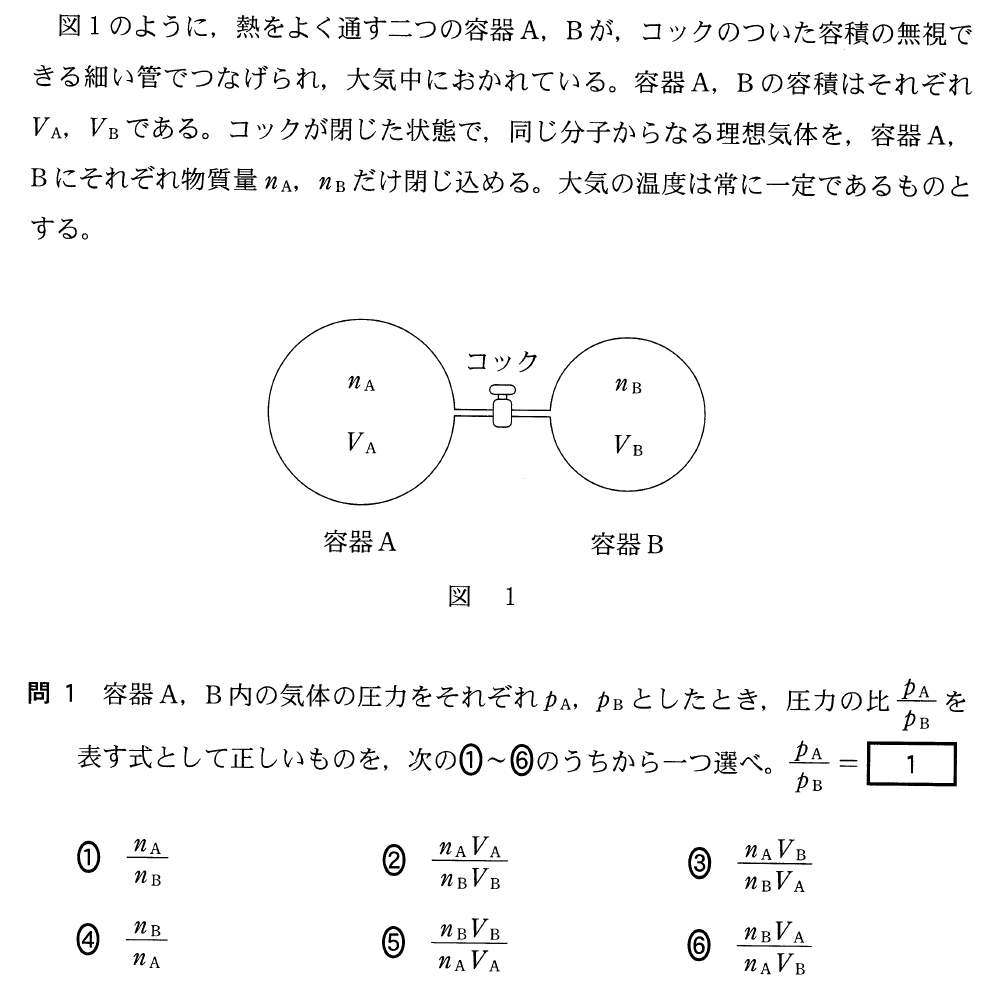
や![]() は約分されて消えるんじゃないかな。ただ、容器Aと容器Bで温度が同じだっていうことは分かる?
は約分されて消えるんじゃないかな。ただ、容器Aと容器Bで温度が同じだっていうことは分かる?
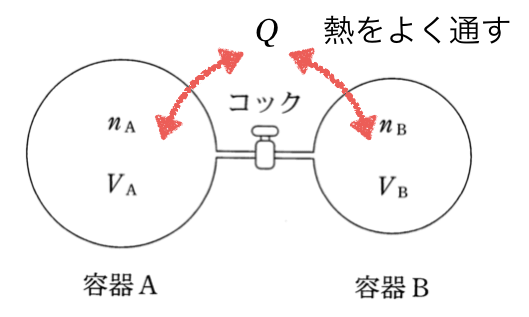
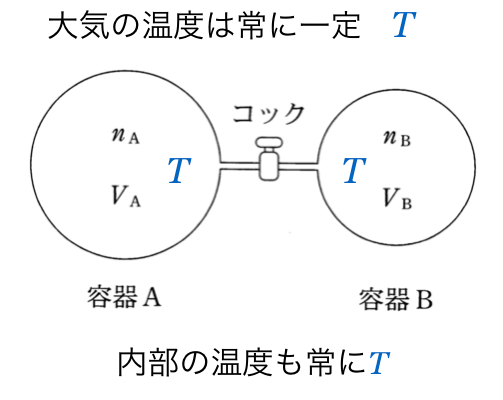
![]() として、気体の状態方程式を立ててみよう。
として、気体の状態方程式を立ててみよう。
![]()
![]()
![]() を求めたいんだから、両辺をそのまま割っちゃえばいいかな。
を求めたいんだから、両辺をそのまま割っちゃえばいいかな。
![]()
![]()
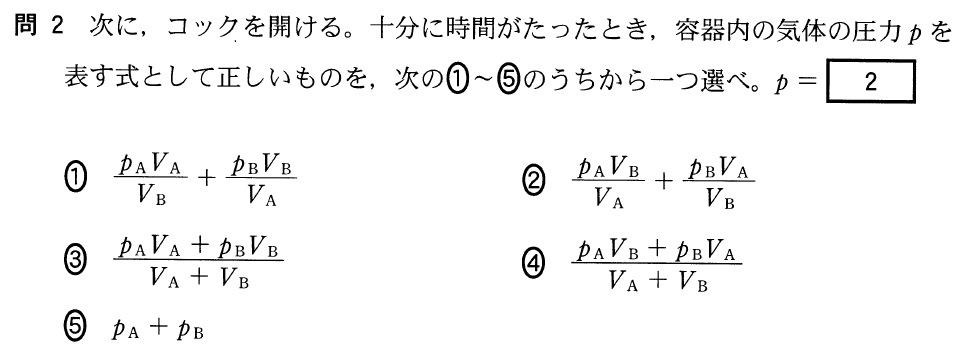
![]() でしょ。モル数も合わせて
でしょ。モル数も合わせて![]() よね。温度はさっき常に
よね。温度はさっき常に![]() だと確認したわよね。
だと確認したわよね。
![]()
![]()
![]() が来るのは良さそうだけど、
が来るのは良さそうだけど、![]() が入っている選択肢はないね。新しく式を立てられたら良いんだけど・・・
が入っている選択肢はないね。新しく式を立てられたら良いんだけど・・・
![]() が選択肢にある
が選択肢にある![]() に変換できればいいのよね。ということは、最初に立てた2本の気体の状態方程式が使えるんじゃない?
に変換できればいいのよね。ということは、最初に立てた2本の気体の状態方程式が使えるんじゃない?
![]()
![]()
![]()
![]()

![]()
![]() が使えるのは、「単原子分子」の時だけなんだ。「単原子分子」についても問題が多いけど、この問題には「単原子分子」っていう言葉は出てこないんだよね。なので、この式は使えないんだ。「単原子分子」とセットで覚えておいてね。
が使えるのは、「単原子分子」の時だけなんだ。「単原子分子」についても問題が多いけど、この問題には「単原子分子」っていう言葉は出てこないんだよね。なので、この式は使えないんだ。「単原子分子」とセットで覚えておいてね。
![]() が、絶対温度
が、絶対温度![]() に比例するっていうことは間違いないんだ。
に比例するっていうことは間違いないんだ。