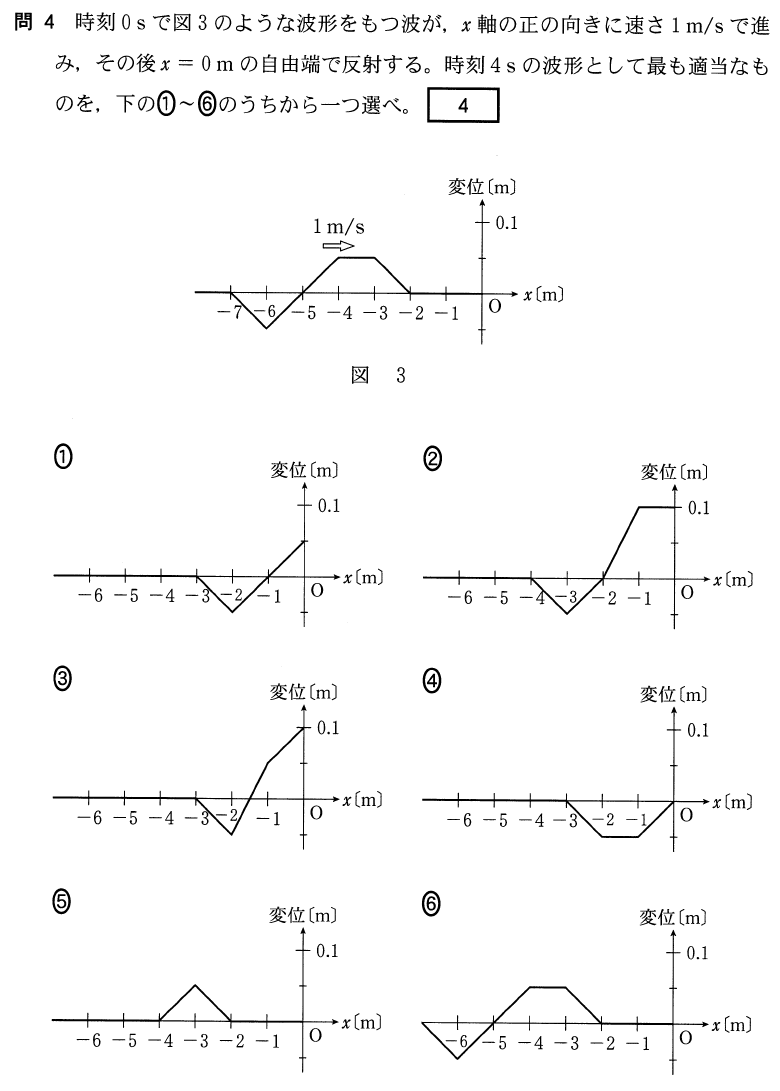
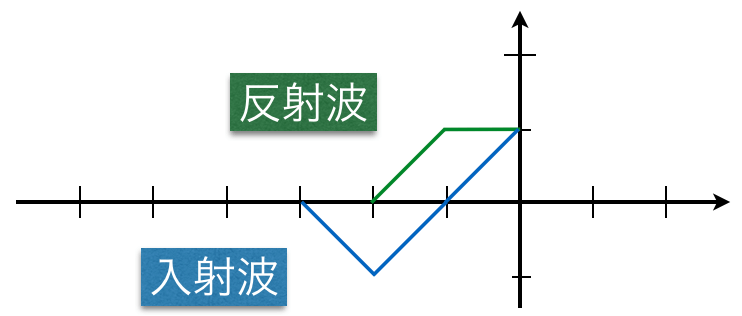
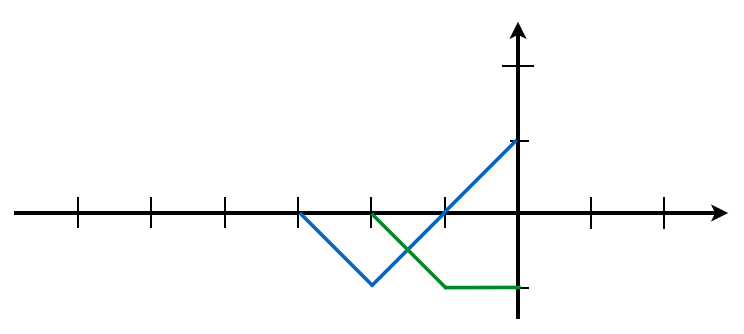
![]() 軸を伸ばさなきゃ描けないということね。こんな感じかな。
軸を伸ばさなきゃ描けないということね。こんな感じかな。
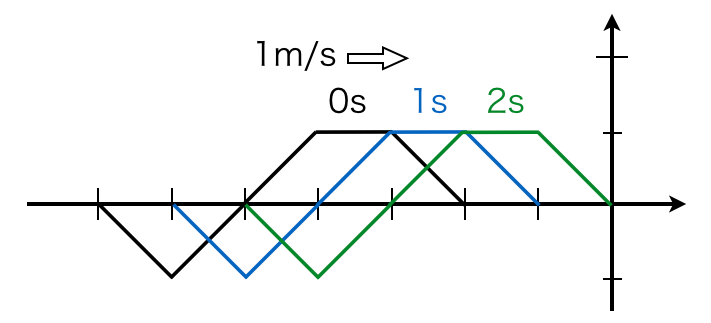
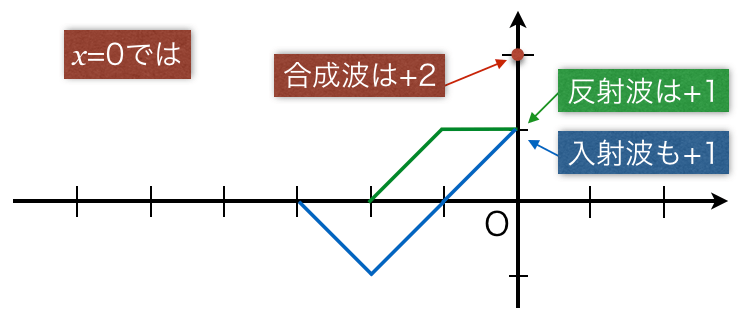
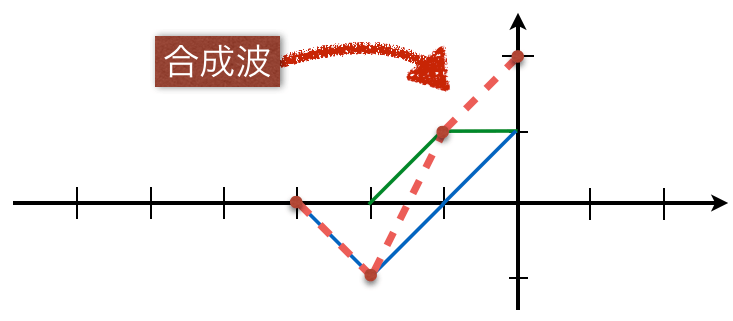
![]() を考えよう。この点では、青色の入射波も、緑色の反射波も、どちらも変位は+1だよね。なので、合わせると変位は+2になるんだ。
を考えよう。この点では、青色の入射波も、緑色の反射波も、どちらも変位は+1だよね。なので、合わせると変位は+2になるんだ。
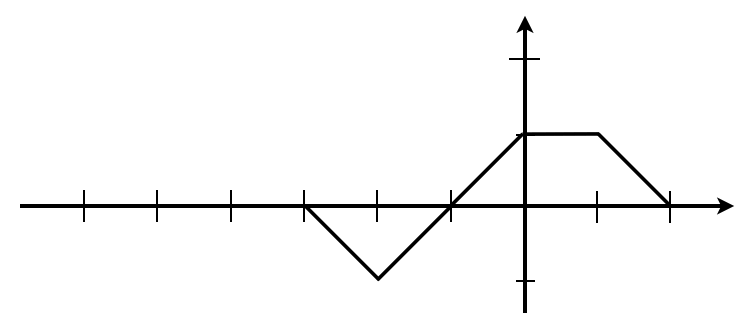
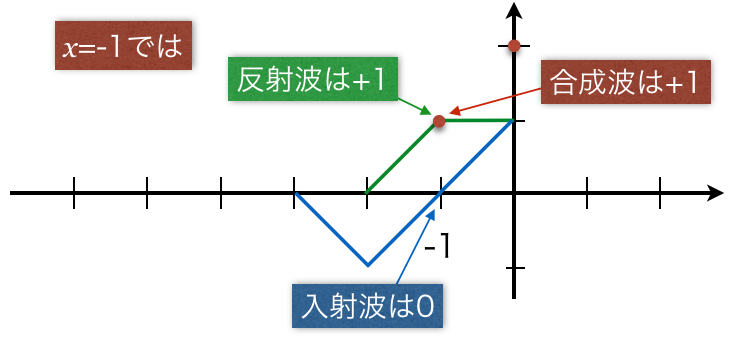
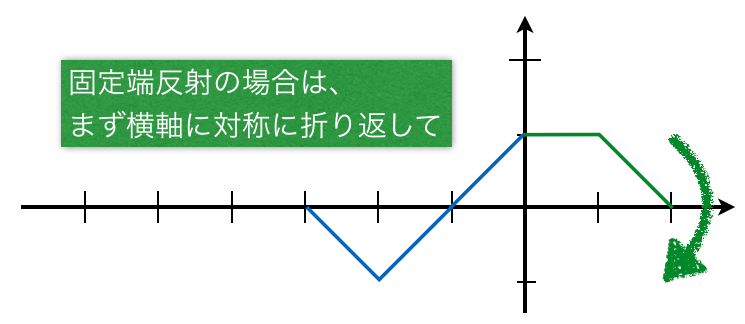
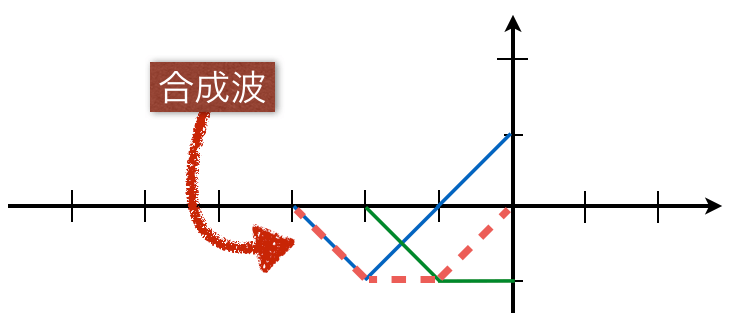
![]() だ。
だ。![]() では、反射波の変位は+1だけど、入射波の変位が0だね。ということは、合成波の変位は+1だね。
では、反射波の変位は+1だけど、入射波の変位が0だね。ということは、合成波の変位は+1だね。
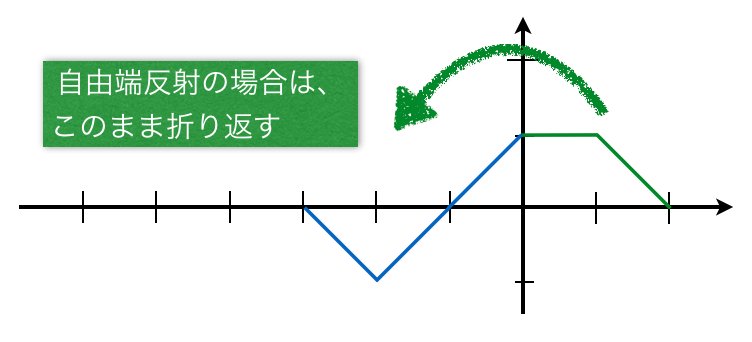
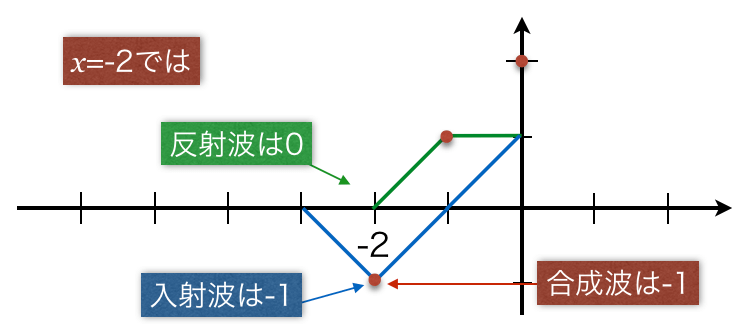
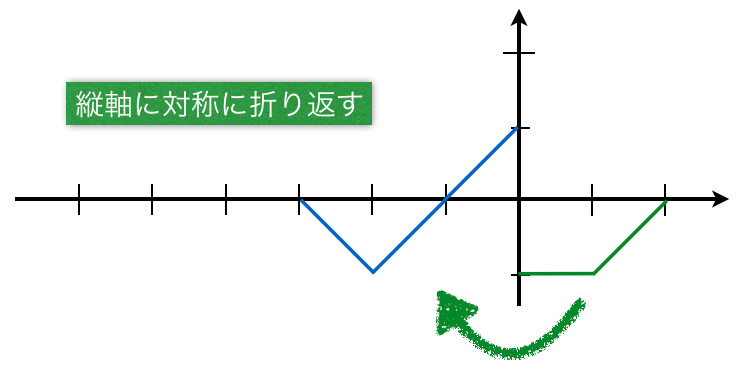
![]() では、反射波の変位は0で、入射波の変位は-1だから、合成波の変位は-1ね。
では、反射波の変位は0で、入射波の変位は-1だから、合成波の変位は-1ね。
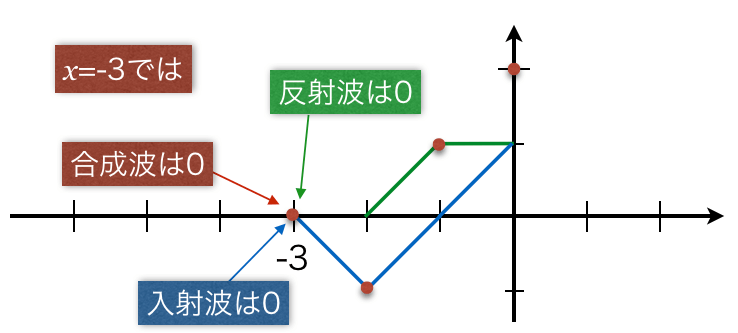
![]() では、反射波も入射波も変位は0ね。もちろん合成波も変位は0。
では、反射波も入射波も変位は0ね。もちろん合成波も変位は0。
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() 軸を伸ばさなきゃ描けないということね。こんな感じかな。
軸を伸ばさなきゃ描けないということね。こんな感じかな。



![]() を考えよう。この点では、青色の入射波も、緑色の反射波も、どちらも変位は+1だよね。なので、合わせると変位は+2になるんだ。
を考えよう。この点では、青色の入射波も、緑色の反射波も、どちらも変位は+1だよね。なので、合わせると変位は+2になるんだ。

![]() だ。
だ。![]() では、反射波の変位は+1だけど、入射波の変位が0だね。ということは、合成波の変位は+1だね。
では、反射波の変位は+1だけど、入射波の変位が0だね。ということは、合成波の変位は+1だね。

![]() では、反射波の変位は0で、入射波の変位は-1だから、合成波の変位は-1ね。
では、反射波の変位は0で、入射波の変位は-1だから、合成波の変位は-1ね。

![]() では、反射波も入射波も変位は0ね。もちろん合成波も変位は0。
では、反射波も入射波も変位は0ね。もちろん合成波も変位は0。





