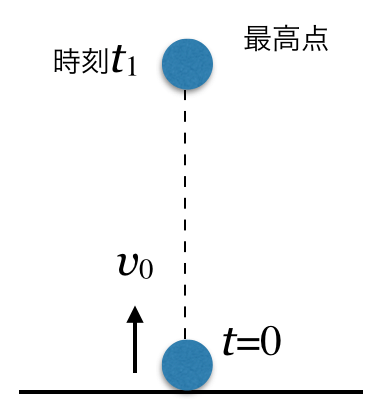
![]() で真上に投げ上げたんだから、
で真上に投げ上げたんだから、
![]() ね。
ね。
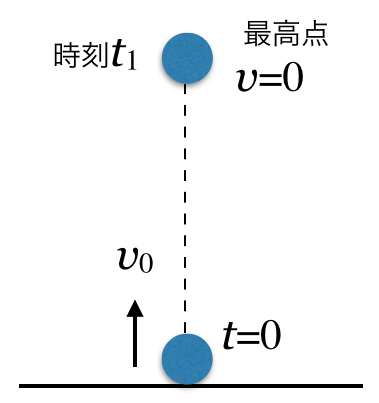
![]() を書いて、正の向きを決めようか。
を書いて、正の向きを決めようか。
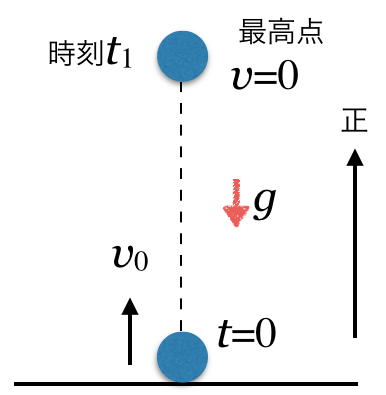
![]() を求めてみようか。そういえば、等加速度直線運動の3つの式を覚えてる?
を求めてみようか。そういえば、等加速度直線運動の3つの式を覚えてる?
![]()
![]()
![]()
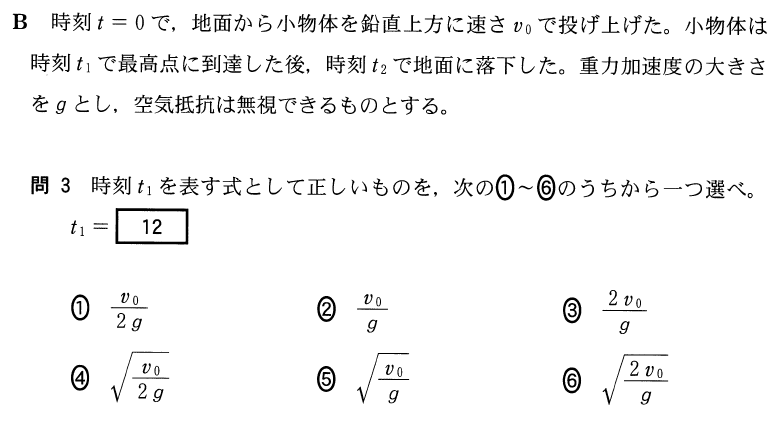
![]() が分かっていて、時間を求めたいんだから、最初の式を使えば良さそうね。正の向きに気をつけて、
が分かっていて、時間を求めたいんだから、最初の式を使えば良さそうね。正の向きに気をつけて、
![]()
![]()
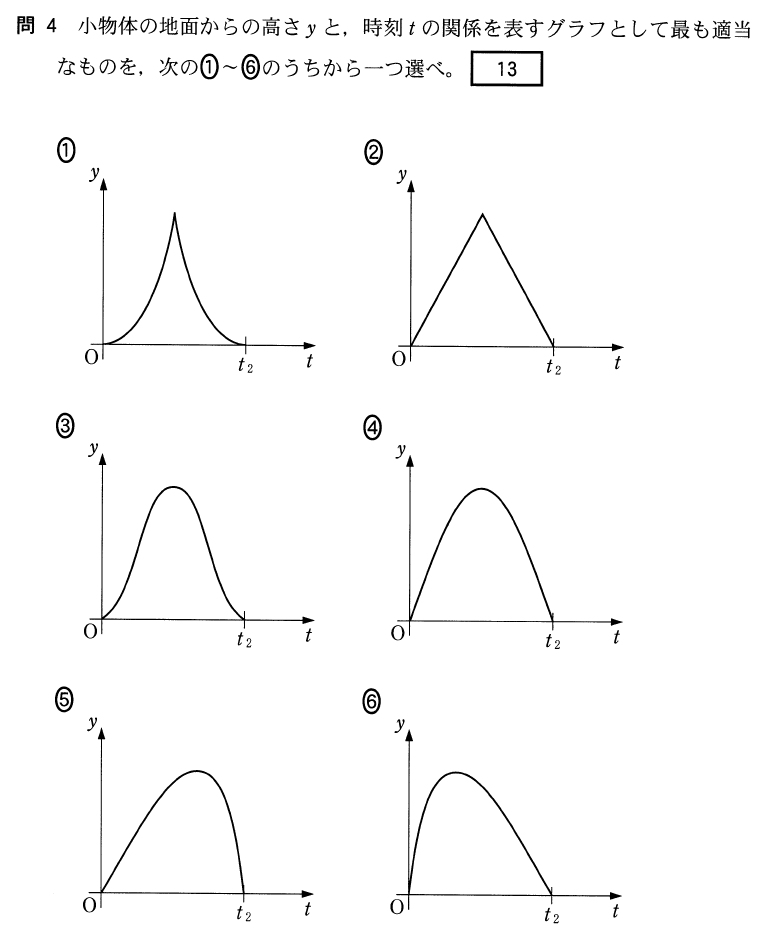
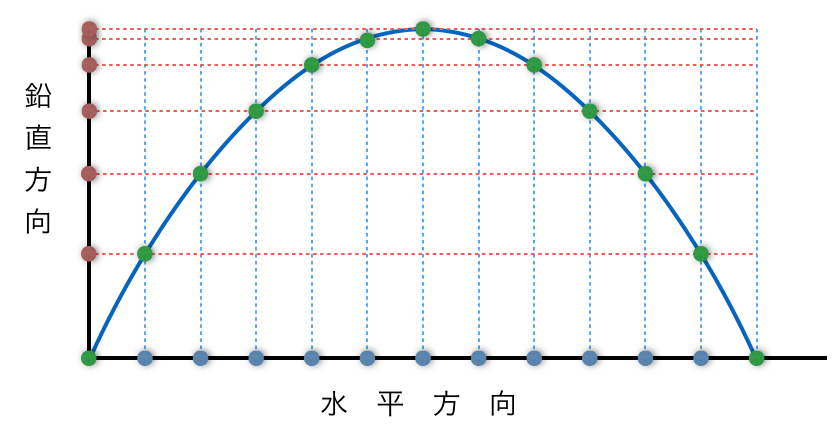
![]() で、横軸は時間
で、横軸は時間![]() だね。
だね。
![]() を
を![]() で表せないか考えるんだ。上手く知ってる関数で表すことができれば、グラフの形はすぐに分かるからね。
で表せないか考えるんだ。上手く知ってる関数で表すことができれば、グラフの形はすぐに分かるからね。
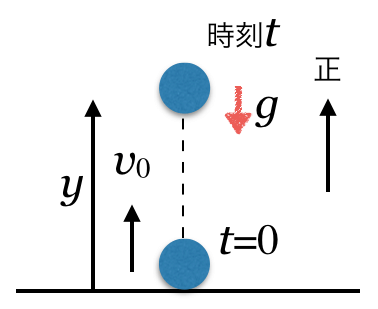
![]()
![]()
![]()
![]() と
と![]() なんだから、2番目の式ね。上向きを正として、
なんだから、2番目の式ね。上向きを正として、
![]()
![]() を
を![]() で表せたじゃない。
で表せたじゃない。
![]()
![]() の項があるから、
の項があるから、![]() の2次関数っていうこと?
の2次関数っていうこと?
![]() の項の係数が「ー」だから、上に凸の放物線かな?
の項の係数が「ー」だから、上に凸の放物線かな?
![]()