
力積を求める問題ね。力積って
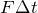
で求めるのよね。
いいね。ちゃんと覚えてるね。でもね、もう一つ力積の求め方があるんだけど覚えていないかな?
私の中には力積は
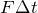
しかないわ。
運動量って
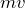
よね。
そうだね。「力積=運動量の変化」って聞いたことないかな?
聞いたことがあるような、ないような・・・まぁ、そのまま式を立ててみよう!
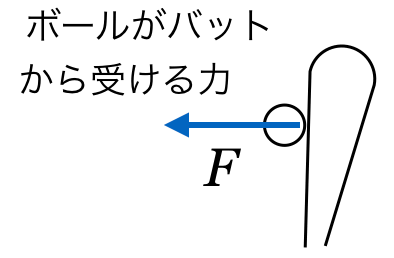
向きを考えなければならないっていうことね。問題文にどっち向きかは書いていないので、最初、右向きに飛んできたとしよう。
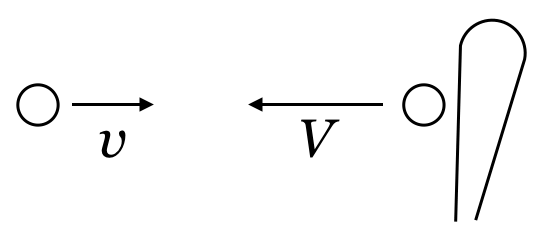
最終的に求めたいのは、ボールが受けた平均の力なので、ボールが受けた力の向きは左になるので、左向きを正にしようかな。
「力積=運動量の変化」なので、
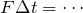
でも、運動量の変化って、どっちからどっちを引くの?
例えば、100gあったものが80gになったとすると、変化量は何g?
-20gっていうこと?じゃあ、80g-100gを計算すれば良いということだから、変化後から変化前を引けばいいってことか。改めて式を立てると、
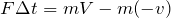
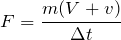

![]() で求めるのよね。
で求めるのよね。![]() しかないわ。
しかないわ。![]() よね。
よね。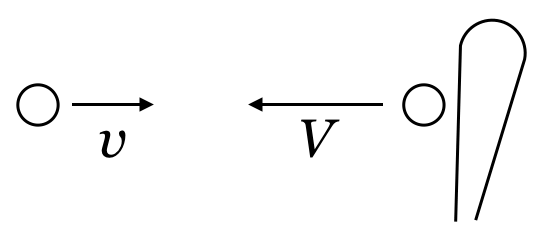

![]() でも、運動量の変化って、どっちからどっちを引くの?
でも、運動量の変化って、どっちからどっちを引くの?![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() で求めるのよね。
で求めるのよね。![]() しかないわ。
しかないわ。![]() よね。
よね。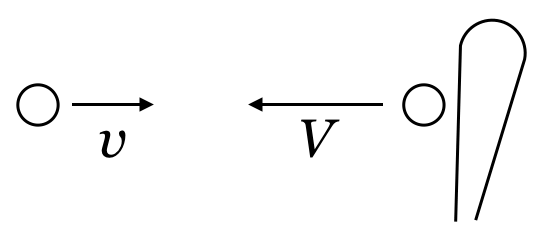

![]() でも、運動量の変化って、どっちからどっちを引くの?
でも、運動量の変化って、どっちからどっちを引くの?![]()
![]()
コメント
[…] 2016年度追試第1問 問1「運動量と力積」 […]