

簡単に言うと、「AP:BPの抵抗の比が自由に変えられる抵抗」だね。抵抗APと抵抗BPが直列になっていると考えて、2つの抵抗の和は一定なんだ。ちなみに回路を描き変えるとこんな感じかな。
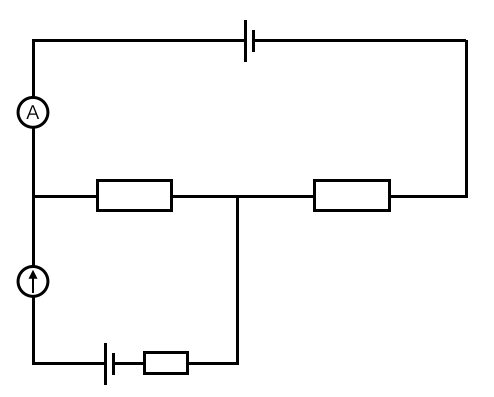
なるほどね。じゃあ次の質問は、検流計に流れる電流が0ってどういうこと?
どういうことって、そういうことだよ。検流計には電流が流れないのよ。
っていうことは、回路を見る限り検流計と電池は直列でつながっているから、電池にも電流が流れていないっていうこと?
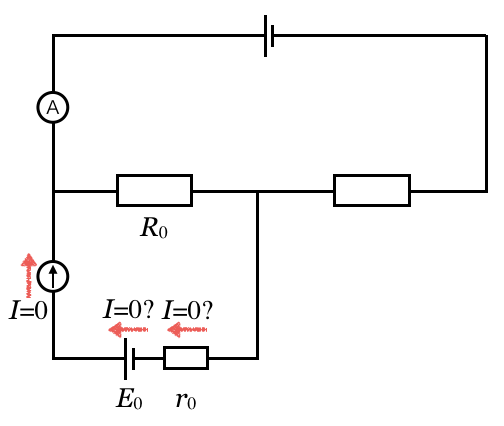
その通りだよ。電池にも、さらには内部抵抗にも電流は流れていないんだね。
だって、電池がつながっているのよ。途中どこかが断線しているっていうわけでもなく、回路の途中に絶縁体やコンデンサーがあるわけでもないのに、電池から電流が流れないの?
気持ちはよく分かるけど、だってそうなんだもん。電池は起電力によって電圧を生じさせるけど、電流が流れるかどうかは回路がどうなっているかによるんだよ。この問題のように電流が流れないときもあるし、電流が逆向きに流れるときもあるよ。
そう言われれば、キルヒホッフの法則を使う問題で電池の向きと電流の向きが逆になったことがあったような気がする。でも逆流するって言うことは、電池は壊れるじゃない!
普通の乾電池だったら壊れるね。でも、充電できる電池だったら、電流が逆流しているというのは、充電しているっていうことなんだよ。
たしかに、「電池」とは書いてあるけど、「普通の乾電池」とは書いていないわね。電池があるのに電流が流れないっていうのは、まだよくイメージができないけど、電流の逆流が充電だというのはよく分かるわ。だとすると電流が0っていうのもあり得そうな気がしてきた。
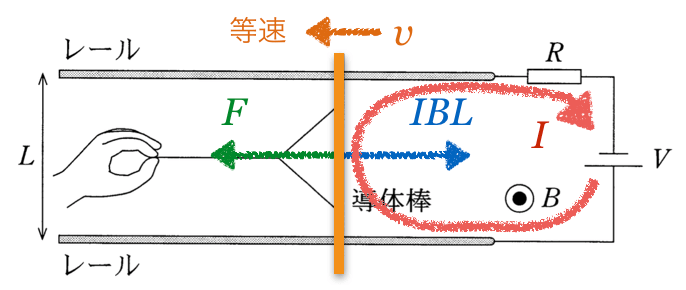
じゃあ、この回路に流れている電流を図に書き入れてみようか。
電流計を流れる電流は
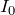
で、回路の下半分には電流が流れないから、すべり抵抗器を流れる電流も
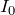
ね。
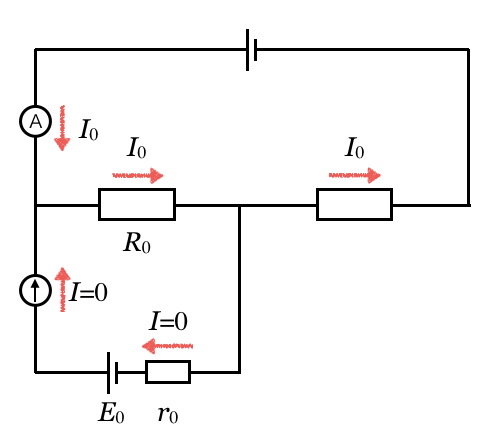
そういうことだね。それじゃあ、最初の空欄
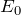
と
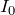
の関係はどうなるかな。
電池には電流が流れていないから、
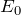
と
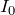
って関係がなさそうだけど・・・
選択肢を見ると、何らかの関係はありそうだね。上にある直流電源の電圧も分からないし、すべり抵抗器の右側、PB間の抵抗も分からないから、できそうなことは限られているね。
できそうなのは、下の回路でキルヒホッフの第2法則の式を立てることかな?
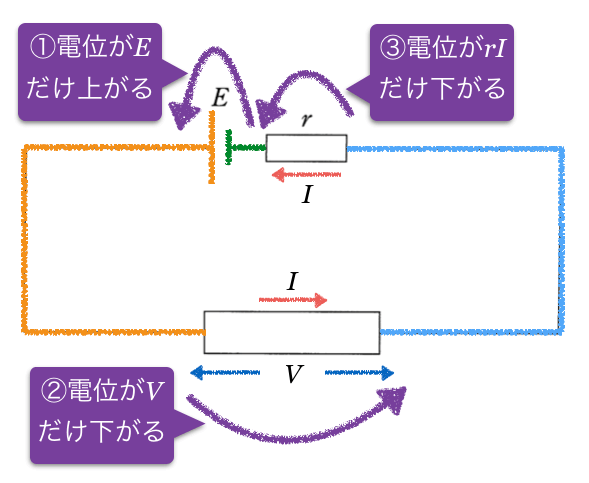
いいね。やってみよう!せっかくだから、前問、問1でやった電位の考え方でやってみない?ルールを確認すると、
(1)つながっている金属は等電位
(2)電流が抵抗を流れると
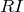
だけ電位が下がる
(3)電池は負極から正極へ電位を

だけ上げる
ということだったね。
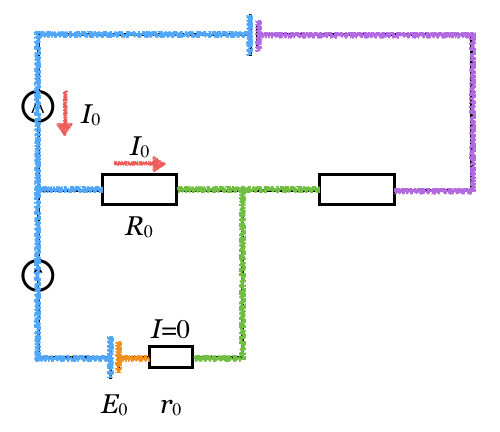
(1)の条件を考えるとそうなるね。(2)の条件を考えると、ちょっと変わらない?
そうか、電池の内部抵抗には電流が流れていないから、電位は下がらないのね。ということは、内部抵抗の左右も等電位ね。
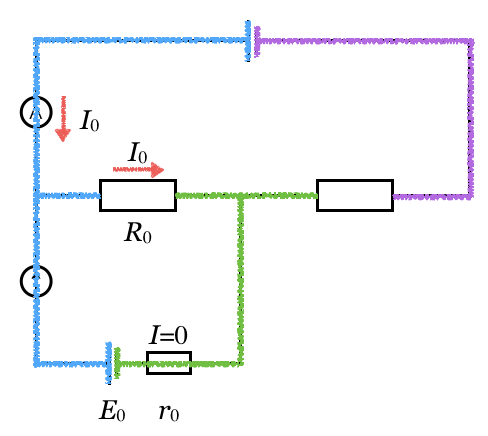
そうなんだよ。図を見ると明らかなように、電池の
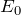
の両端の色と、すべり抵抗器の
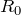
の両端の色が同じでしょ。
ほんとだ。両端の色が同じということは、電位差が同じということね。式で表すと
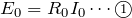
問題文の続きを読むと、結局は電池の起電力
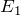
、内部抵抗
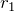
、検流計を流れる電流0、電流計を流れる電流
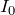
よね。AP間の抵抗を
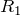
とすると、こんな図で良いかな?
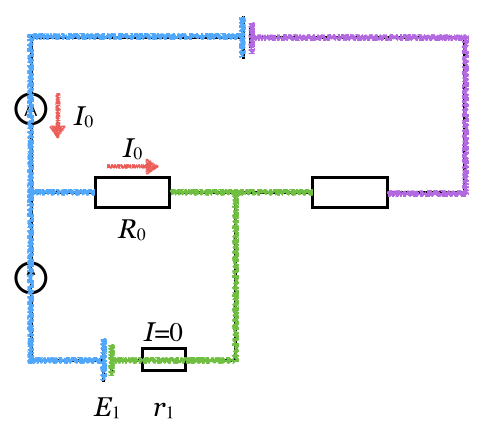
そうだね。検流計を流れる電流が0なので、各値は変わるけど電位の図は変わらないね。
まず大小関係で分かっているのは、AP間の抵抗ね。Pを右に移動させたんだから、抵抗値は大きくなっているのよね。なので、
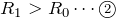
あとは、最初の空欄と同様に電池の起電力
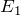
の両端の電位差と、AP間の電位差
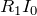
が等しいから、
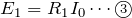
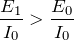
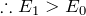
あとは①と③から
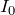
を消去すればいいのかな。①÷③をやっちゃうと、
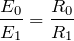
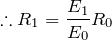




![]() で、回路の下半分には電流が流れないから、すべり抵抗器を流れる電流も
で、回路の下半分には電流が流れないから、すべり抵抗器を流れる電流も![]() ね。
ね。
![]() と
と![]() の関係はどうなるかな。
の関係はどうなるかな。![]() と
と![]() って関係がなさそうだけど・・・
って関係がなさそうだけど・・・![]() だけ電位が下がる
だけ電位が下がる![]() だけ上げる
だけ上げる 

![]() の両端の色と、すべり抵抗器の
の両端の色と、すべり抵抗器の![]() の両端の色が同じでしょ。
の両端の色が同じでしょ。![]()
![]() 、内部抵抗
、内部抵抗![]() 、検流計を流れる電流0、電流計を流れる電流
、検流計を流れる電流0、電流計を流れる電流![]() よね。AP間の抵抗を
よね。AP間の抵抗を![]() とすると、こんな図で良いかな?
とすると、こんな図で良いかな?
![]()
![]() の両端の電位差と、AP間の電位差
の両端の電位差と、AP間の電位差![]() が等しいから、
が等しいから、![]()
![]()
![]()
![]() を消去すればいいのかな。①÷③をやっちゃうと、
を消去すればいいのかな。①÷③をやっちゃうと、![]()
![]()


コメント
[…] 2016年度追試第2問A問2「すべり抵抗器を含む回路」 […]