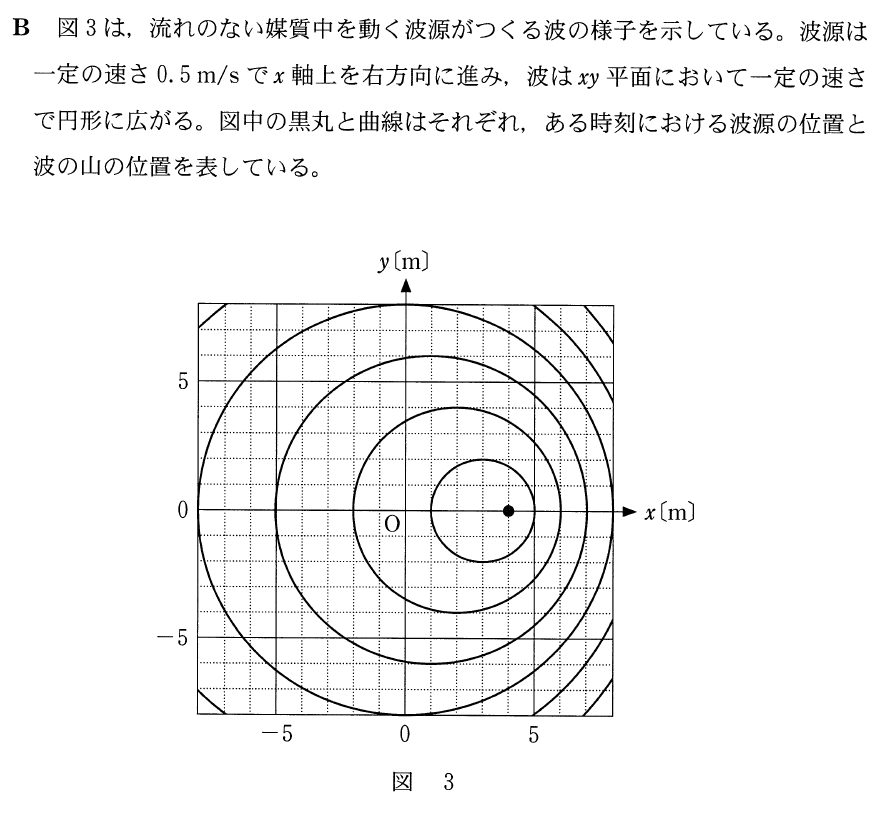

ドップラー効果のところでこんな図を見たことがあるわ。
おっ、よく分かってるね。まさしくドップラー効果の説明で使う図だけど、この問題ではドップラー効果の公式は使う必要がないね。
ドップラー効果の公式を使わないとすると、何からやればいいのか全く分からないわ。
まずは図をきちんと理解するところから始めよう。今、波源はどこにいるかな?
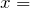
4mの黒丸のところね。
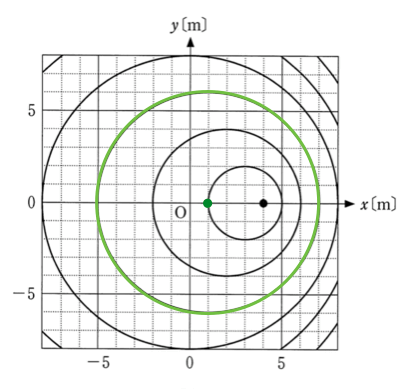
そうだね。じゃあ、一番小さい円は何を表しているかな。
この円は波の山を表しているのよね。一番小さい円の中心は、
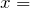
3mだから、波源が
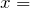
3mにいたときに出た波かな?
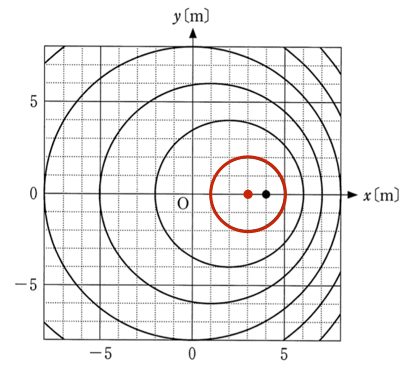
そういうことだよね。波源が
3mで波を出してから最初の図の位置
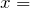
4mに移動するまでにどのくらい時間がかかっているかな?
時間?そんなこと分かるの?1m動いたっていうことは分かるけど。
そうか、波源の速さは0.5m/sだった。1m進むには2秒ね。
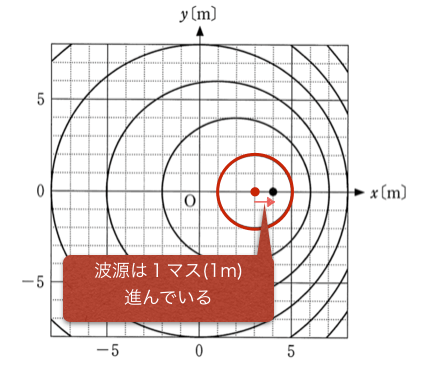
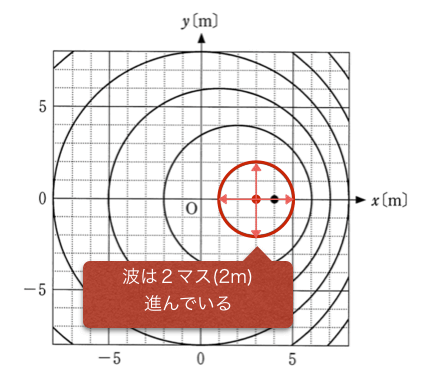
なるほど。波源が1m進んでいる間に、波は2m進んでいるのね。
波源が
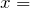
2mにいたときに出した波ね。
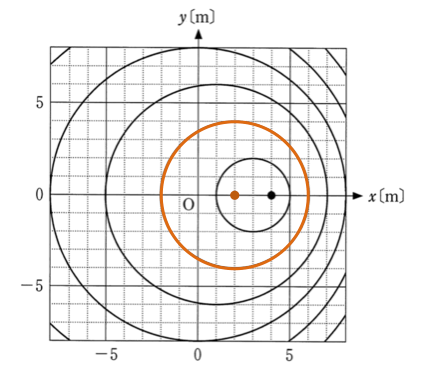
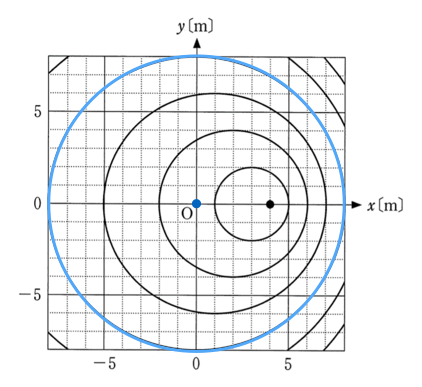
同様に考えると、3番目の円は波源が
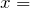
1mにいたときに出した波、4番目の円は波源が原点にいたときに出した波だね。
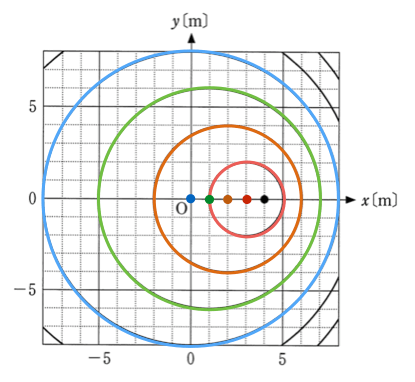
ということは、この波源は1m進むごとに、つまり2秒ごとに1つ波を出しているっていうことね。
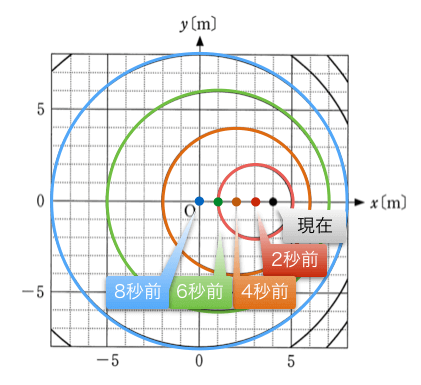
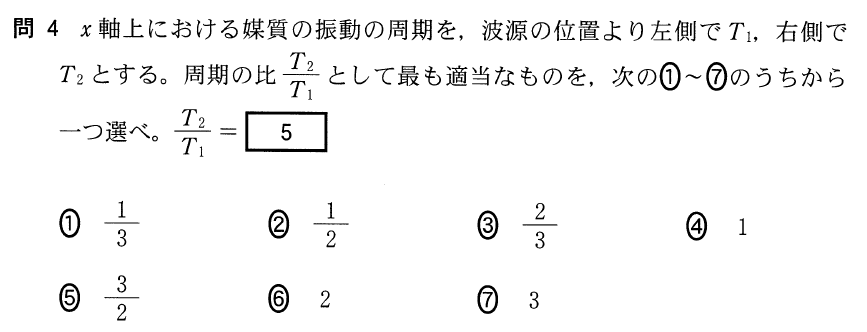
選択肢に「1」っていうのがあるから、同じかもしれないけど、最初に気づいたように、この図ってドップラー効果の説明に使う図だよね。ということは、波源が進む方向と、波源が遠ざかる方向では振動数が違うよね。振動数が違うっていうことは、
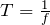
なんだから、周期も違うよね。
まぁそうだね。周期の求め方はいろいろとありそうだけど、例えばさっき使わないって言ったけどドップラー効果の公式を上手く使うとか、さっき使った
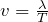
を使うとかね。今は簡単に図から求めてみよう。
少しは考えなきゃダメだけどね。まぁたいしたこと無さそうだよ。この波って1マス進むのに、何秒かかるか分かるかな。
波源は2秒で1マス進むけど、波はその2秒間で2マス進むのよね。さっき描いた図だとこんな感じ。
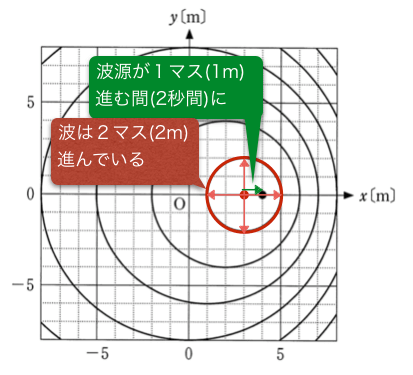
それが分かればもうあとは簡単。波源の右側でこの波を観察するとしよう。この図の×のところね。
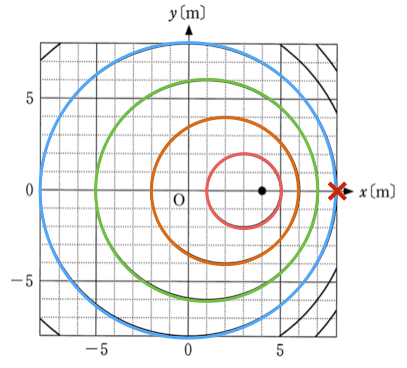
波は2秒で2マス進むから、1秒で1マス。ということは、波の山は1秒ごとに来そうね。
気を緩めちゃダメっていうことね。
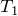
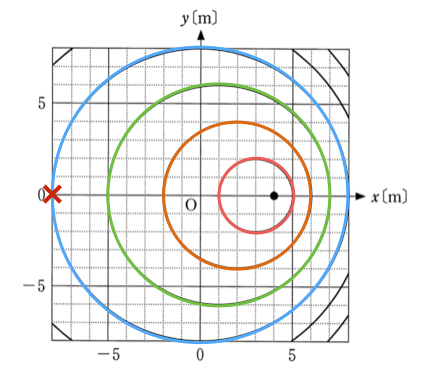
は波源の左側、
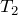
が波源の右側なので、
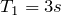
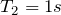
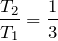


![]() 4mの黒丸のところね。
4mの黒丸のところね。![]() 3mだから、波源が
3mだから、波源が![]() 3mにいたときに出た波かな?
3mにいたときに出た波かな?
![]() 3mで波を出してから最初の図の位置
3mで波を出してから最初の図の位置![]() 4mに移動するまでにどのくらい時間がかかっているかな?
4mに移動するまでにどのくらい時間がかかっているかな?

![]() 2mにいたときに出した波ね。
2mにいたときに出した波ね。
![]() 1mにいたときに出した波、4番目の円は波源が原点にいたときに出した波だね。
1mにいたときに出した波、4番目の円は波源が原点にいたときに出した波だね。




![]() なんだから、周期も違うよね。
なんだから、周期も違うよね。![]() を使うとかね。今は簡単に図から求めてみよう。
を使うとかね。今は簡単に図から求めてみよう。


![]() は波源の左側、
は波源の左側、![]() が波源の右側なので、
が波源の右側なので、![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() 4mの黒丸のところね。
4mの黒丸のところね。![]() 3mだから、波源が
3mだから、波源が![]() 3mにいたときに出た波かな?
3mにいたときに出た波かな?
![]() 3mで波を出してから最初の図の位置
3mで波を出してから最初の図の位置![]() 4mに移動するまでにどのくらい時間がかかっているかな?
4mに移動するまでにどのくらい時間がかかっているかな?

![]() 2mにいたときに出した波ね。
2mにいたときに出した波ね。
![]() 1mにいたときに出した波、4番目の円は波源が原点にいたときに出した波だね。
1mにいたときに出した波、4番目の円は波源が原点にいたときに出した波だね。




![]() なんだから、周期も違うよね。
なんだから、周期も違うよね。![]() を使うとかね。今は簡単に図から求めてみよう。
を使うとかね。今は簡単に図から求めてみよう。


![]() は波源の左側、
は波源の左側、![]() が波源の右側なので、
が波源の右側なので、![]()
![]()
![]()
コメント
[…] 2016年度追試第3問B「移動する波源と周期」 […]