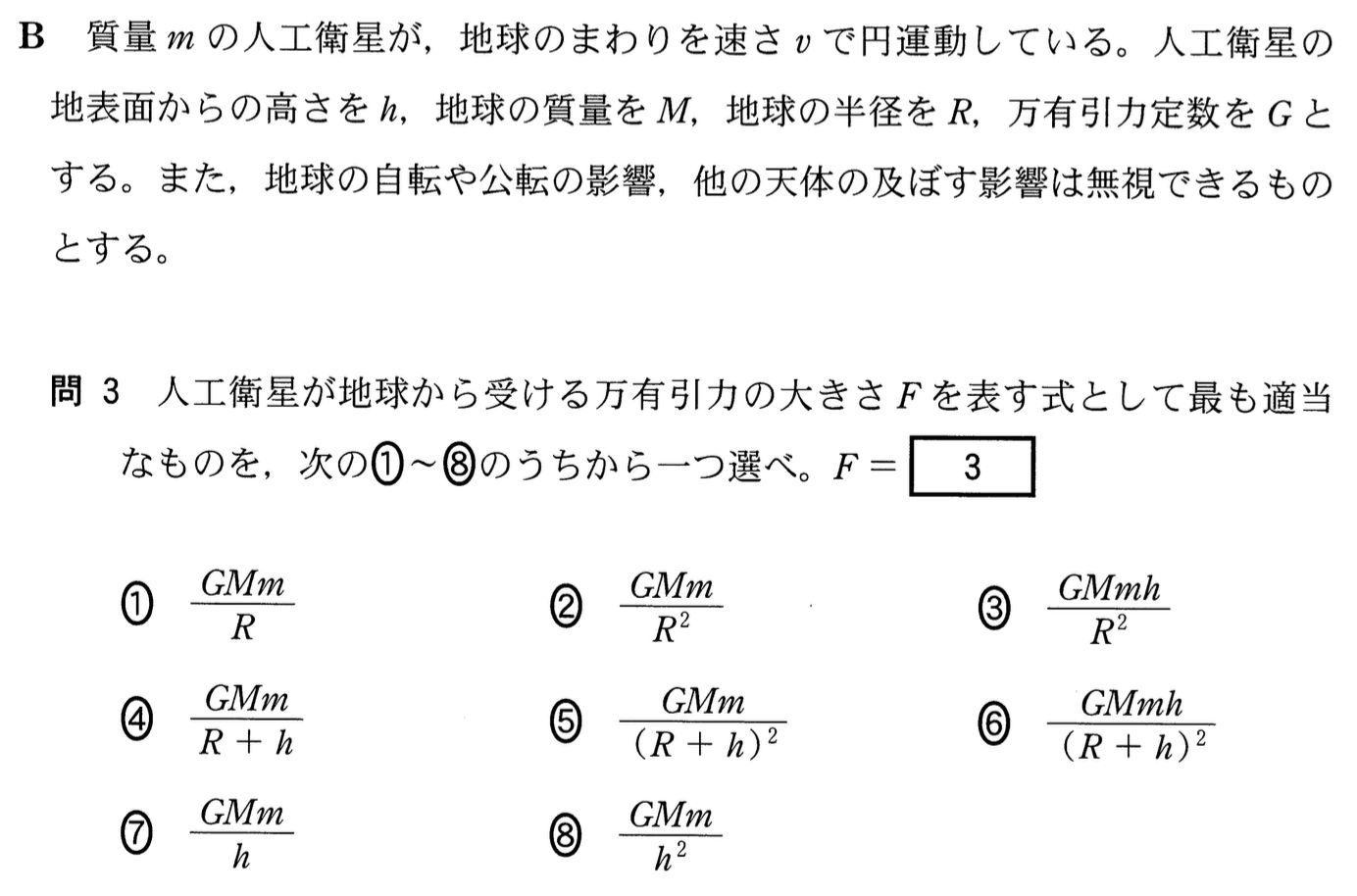
地球と人工衛星との万有引力の問題だね。万有引力の公式は覚えているかな。
雰囲気は覚えているんだけど・・・こんな感じだったっけ?
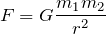
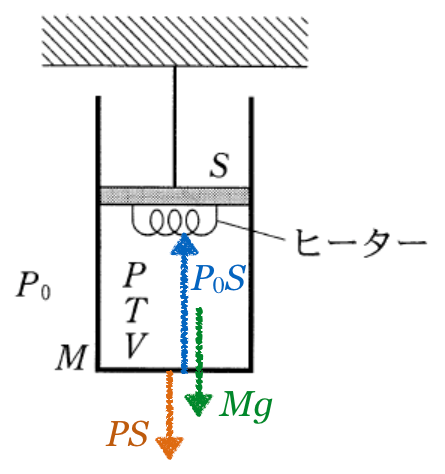
その通りだ。大丈夫だね。あとはこの問題には図がないので、図を描いてみよう。
人工衛星は地表面から
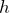
の高さを飛んでいるのね。こんな感じかな。
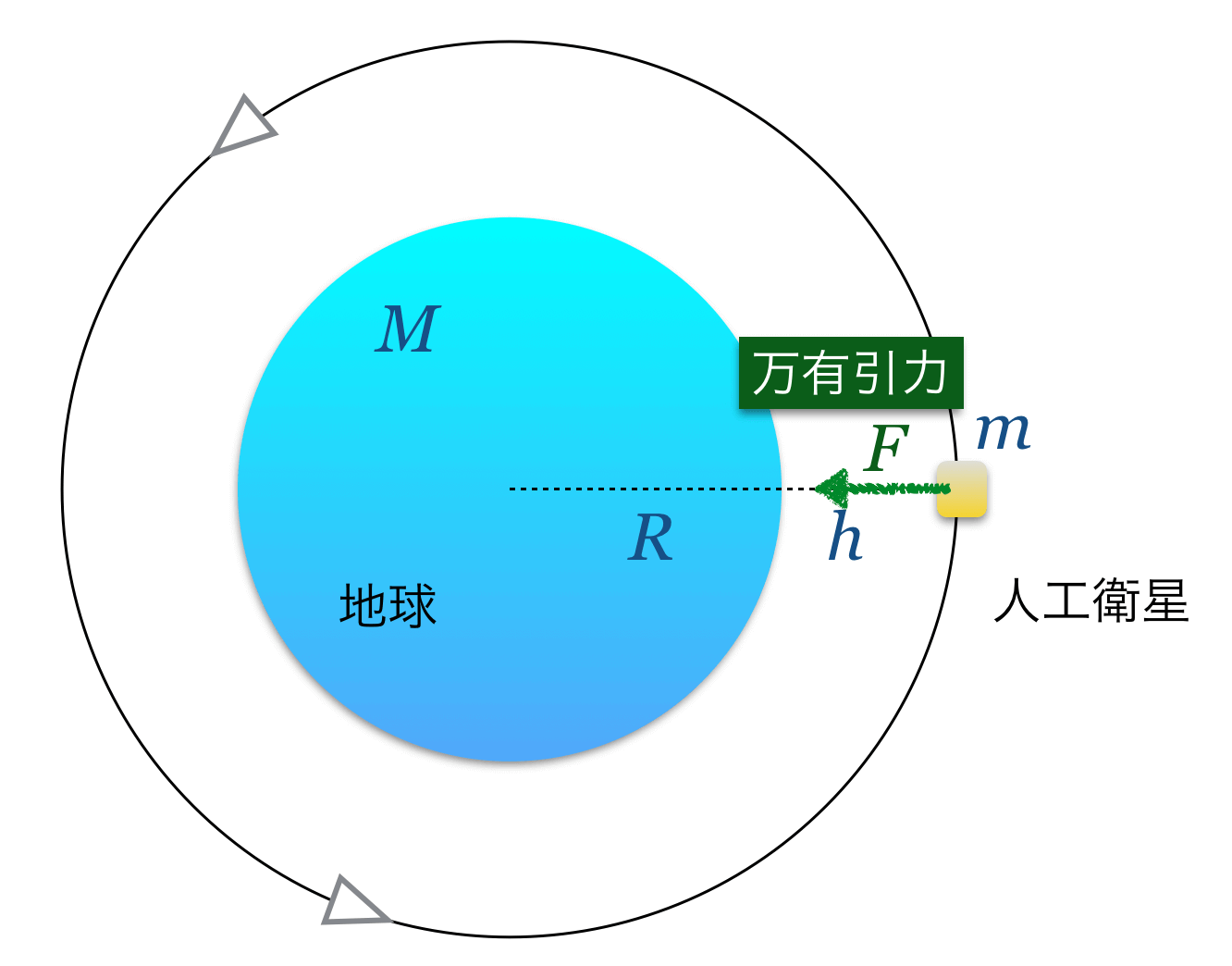
いい感じの図になったね。じゃあ、万有引力を求めてみようか。
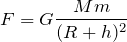
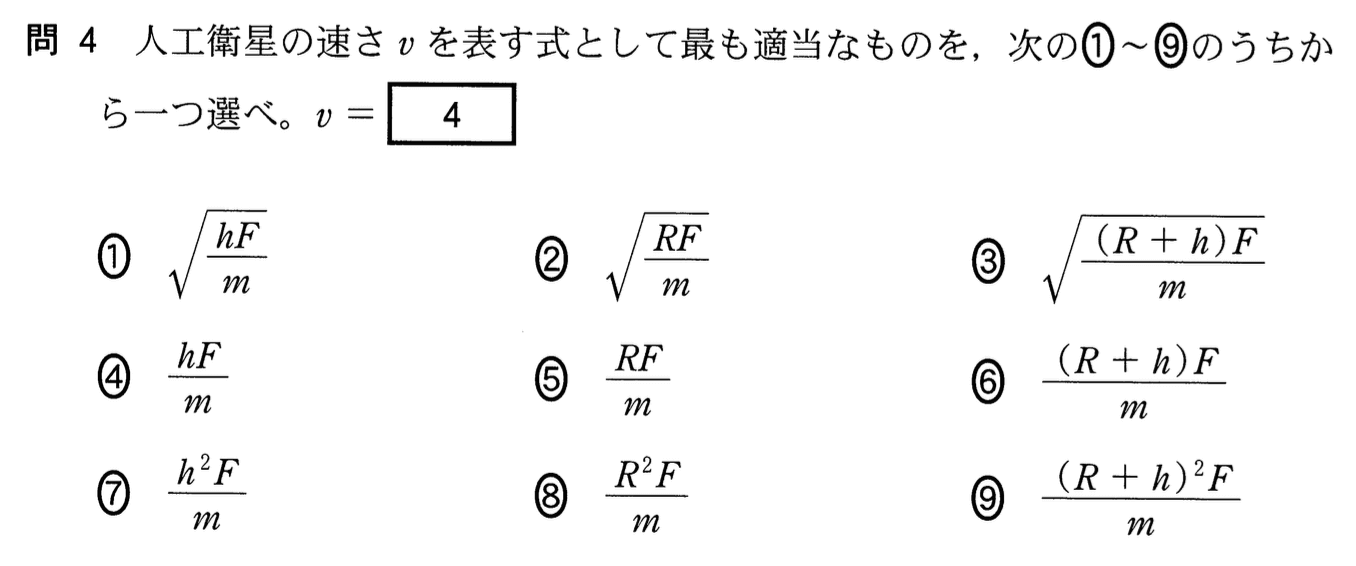
万有引力で動いているときの、速さってどうやって求めるんだっけ?
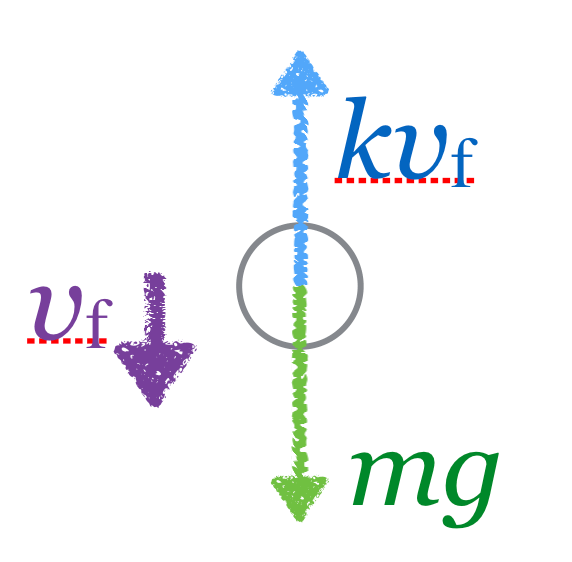
万有引力というよりも、円運動で考えた方が良いんじゃないかな?
円運動ね。じゃあさっきの図に速度

と、加速度
を加えると、
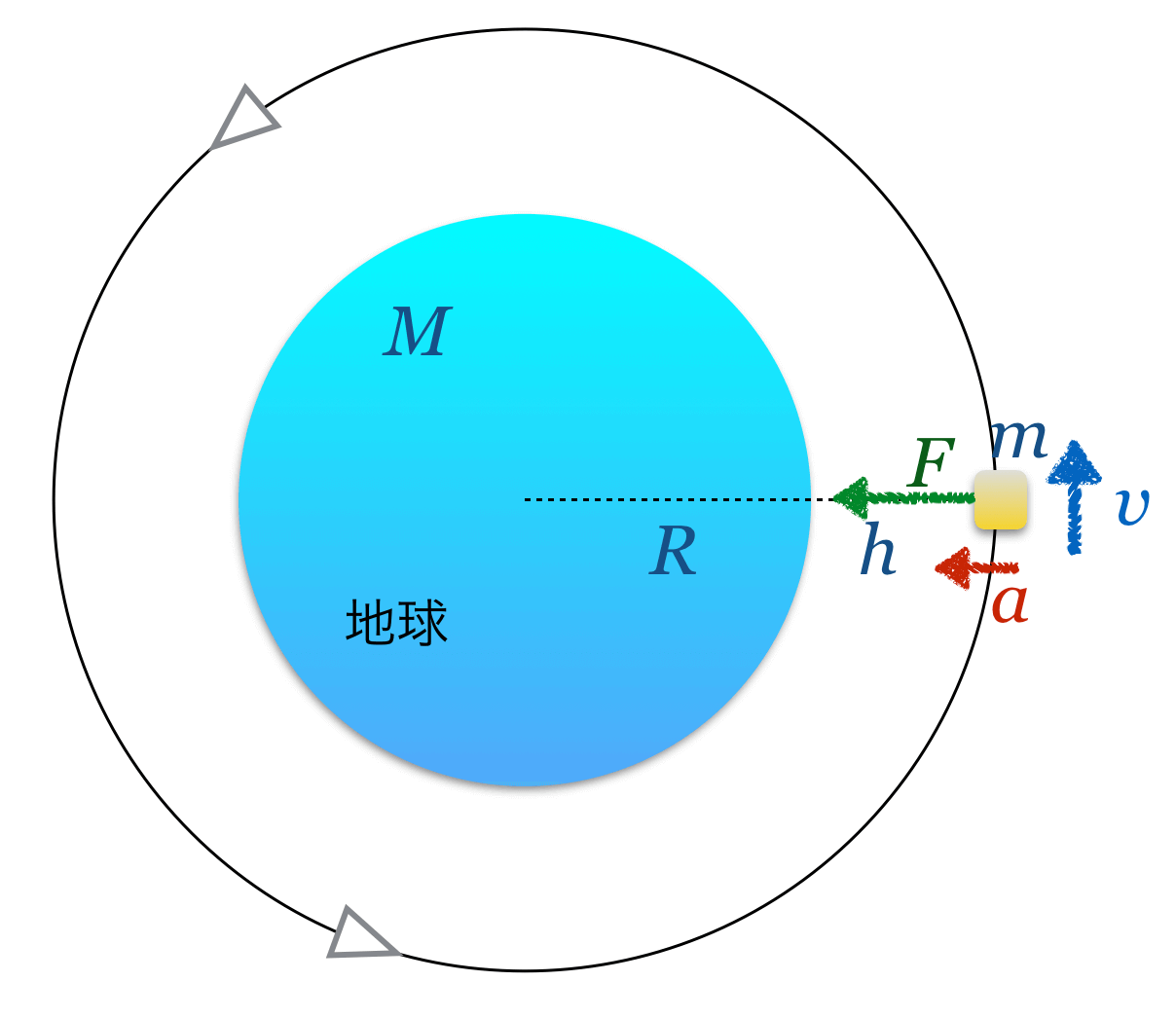
そうだね。円運動の速度は接線方向、加速度は円の中心方向だね。次はどうしよう。
とりあえずは運動方程式かな。
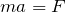
だから、円の中心方向を正として、
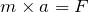
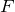
は万有引力だから、問3の答えを入れればいいんだけど、選択肢を見ると、
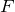
をそのまま使っているようなので、これは残しておこうかな。あとは
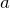
ね。円運動の加速度の公式は、
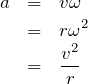
とあるけど、今は

は関係なさそうなので、最後の式を使おうかな。円運動の半径は
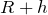
なので、
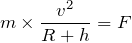
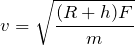

この問題は、どういうこと?
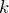
は

と
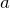
で表されているから、答えは⑤の
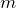
にも

にもよらないんじゃない?こんな問題?
そんな問題だといいんだけどね。実際は
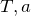
が
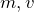
で表せないか分析しなきゃダメなんだね。
でもね、問題文1行目の「惑星の運動に関する法則」ってどんな法則か知らない?
そうだね。ケプラーの法則って、第1から第3まであるんだけど、3つがどんな法則か覚えてるかな?
あ〜、あんまり覚えていないけど、惑星は楕円軌道を描くってあったような気がする。
第1法則だね。正確には「惑星は太陽をひとつの焦点とする楕円軌道を描く」っていう法則だ。第2法則は「面積速度一定の法則」。詳しいことは調べてみてね。
第3法則が実は、この問題の設問そのものだ。「惑星の公転周期

の2乗は、楕円軌道の半長軸
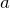
の3乗に比例する」っていう法則だからね。
この法則が人工衛星と地球の間にも成り立つと言っているのね。この問題で人工衛星は円軌道としているけど同じよね。

の2乗と、地球の中心からの距離
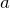
の3乗の比は一定なのよね。つまり答えはやっぱり⑤ということね。
そういうことなんだよ。でもせっかくだから計算しておいてもいいかな。一応ケプラーの第3法則の証明っていうことで。
簡単じゃないけど、順番に計算していけばたどり着くよ。まず
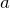
はこの問題ではどうなる?
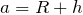
そうだね。次は

だけど、円運動の周期の式を使うと、この問題ではどうなるかな?
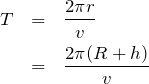
そうだね。ということは、
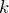
を計算してみると、
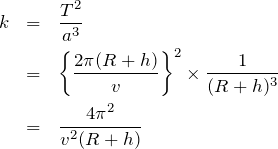
まず問4の答えに問3の答えを代入して
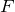
を消去しよう。
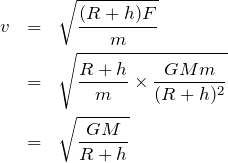
これをさっきの
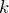
の式に代入しよう。
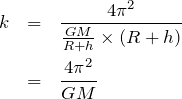
となって、
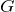
は定数だし、
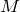
は地球の質量なので決まった値だよね。つまり、
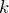
は

や
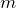
によらず一定ということだね。いずれにしも、答えは⑤だ。

![]()
![]() の高さを飛んでいるのね。こんな感じかな。
の高さを飛んでいるのね。こんな感じかな。
![]()

![]() と、加速度
と、加速度![]() を加えると、
を加えると、
![]() だから、円の中心方向を正として、
だから、円の中心方向を正として、![]()
![]() は万有引力だから、問3の答えを入れればいいんだけど、選択肢を見ると、
は万有引力だから、問3の答えを入れればいいんだけど、選択肢を見ると、![]() をそのまま使っているようなので、これは残しておこうかな。あとは
をそのまま使っているようなので、これは残しておこうかな。あとは![]() ね。円運動の加速度の公式は、
ね。円運動の加速度の公式は、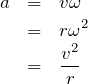
![]() は関係なさそうなので、最後の式を使おうかな。円運動の半径は
は関係なさそうなので、最後の式を使おうかな。円運動の半径は![]() なので、
なので、![]()
![]()

![]() は
は![]() と
と![]() で表されているから、答えは⑤の
で表されているから、答えは⑤の![]() にも
にも![]() にもよらないんじゃない?こんな問題?
にもよらないんじゃない?こんな問題?![]() が
が![]() で表せないか分析しなきゃダメなんだね。
で表せないか分析しなきゃダメなんだね。![]() の2乗は、楕円軌道の半長軸
の2乗は、楕円軌道の半長軸![]() の3乗に比例する」っていう法則だからね。
の3乗に比例する」っていう法則だからね。![]() の2乗と、地球の中心からの距離
の2乗と、地球の中心からの距離![]() の3乗の比は一定なのよね。つまり答えはやっぱり⑤ということね。
の3乗の比は一定なのよね。つまり答えはやっぱり⑤ということね。![]() はこの問題ではどうなる?
はこの問題ではどうなる?![]()
![]() だけど、円運動の周期の式を使うと、この問題ではどうなるかな?
だけど、円運動の周期の式を使うと、この問題ではどうなるかな?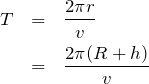
![]() を計算してみると、
を計算してみると、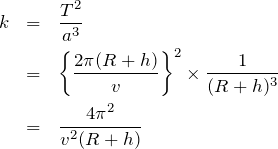
![]() があるので、
があるので、![]() は
は![]() に反比例するのね。
に反比例するのね。![]() を消去しよう。
を消去しよう。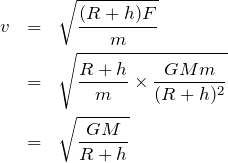
![]() の式に代入しよう。
の式に代入しよう。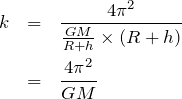
![]() は定数だし、
は定数だし、![]() は地球の質量なので決まった値だよね。つまり、
は地球の質量なので決まった値だよね。つまり、![]() は
は![]() や
や![]() によらず一定ということだね。いずれにしも、答えは⑤だ。
によらず一定ということだね。いずれにしも、答えは⑤だ。

コメント
[…] 2016年度追試第4問B「万有引力」 […]