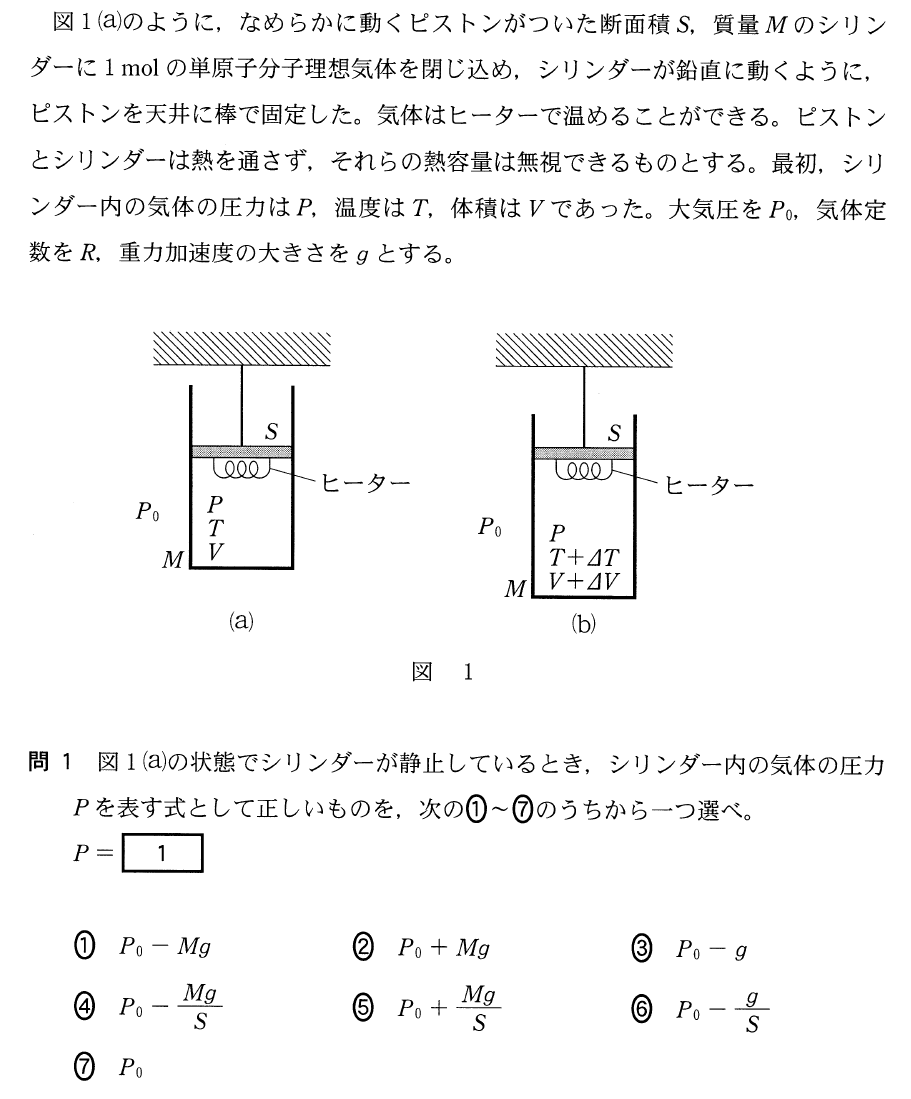
ピストンが固定されていて、シリンダーが動くっていうこと?
そうだね。シリンダーとピストンの問題は、普通ピストンにはたらく力の矢印を描くんだけど、この問題はシリンダーにはたらく力を描かなきゃダメだね。描いてみようか。
まず、重力を描きたいんだけど、こういう場合はどこから描けばいいの?
この図でいうとシリンダーがコの字になっているので描きにくいけど、重心はだいたい真ん中でいいのね。
真ん中よりちょっと下っていう感じでいいんじゃないかな。
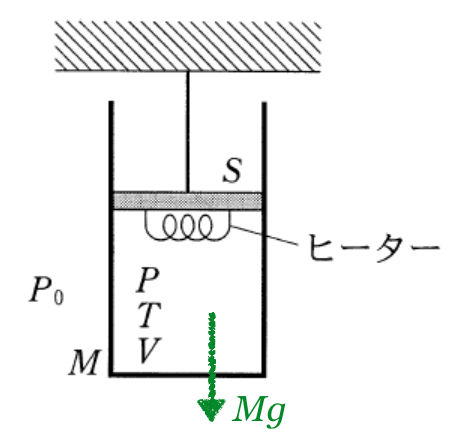
重力があるのに、シリンダーが静止しているのは、何かが上向きにシリンダーを引っ張っているからよね。
空気って分子が飛び回っているんだよね。どうやって引っ張るの?
ん〜良く分からないけど、引っ張るとすれば空気しかないでしょ。
気体分子は壁にぶつかるしかないので、押すことしかできないんだ。だから、シリンダーを引っ張る力は何もないよ。
シリンダーの外の気体の押す力が大きいからだね。大気圧が
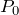
だから、シリンダーを押す力はいくらになるかな?
そもそも圧力って、力÷面積だから、押す力は圧力×面積よね。ただ大気圧って、いろんな方向から押すっていうこと?
確かにいろんな方向から押すんだけど、今はシリンダーが落ちない原因としての大気圧なので、上向きの力だけでいいんじゃないかな?
そうね。シリンダーは断面積が
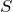
なので、上向きの力は
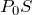
ね。
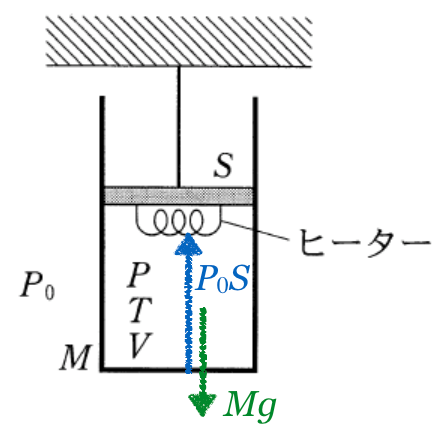
さっきの話からすると、中の気体もシリンダーを押しているのよね。下向きの力だけ考えると、これでいいかな?
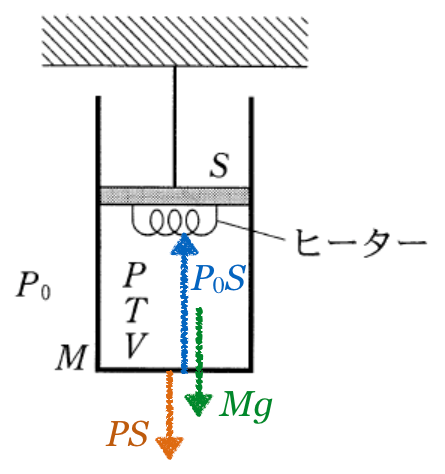
一応横向きの力もあるけど、360°同じ大きさの力を受けているので、つりあっているんだね。
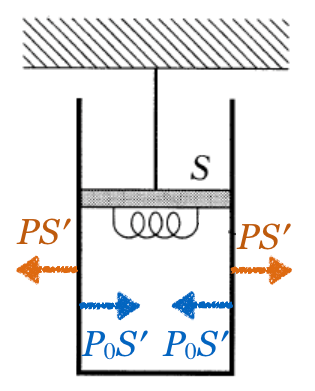
それじゃあ、下向きを正としてつりあいの式を立てようか。
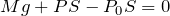
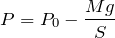

何となく覚えているんだけど、条件があったんじゃなかったっけ。
そうだね。内部エネルギー
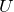
の式で覚えなければならない式は1つだけなんだけど、「単原子分子理想気体」の場合という条件付きで、
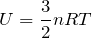
だね。この問題では「1molの単原子分子理想気体」と書かれているのと、求めたいのは内部エネルギーの増加分
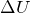
だということで、どうなるかな?
温度は

だけ温度が上昇しているので、
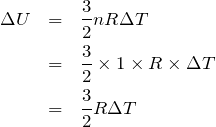
その通り!選択肢は⑦〜⑨に絞られたね。
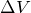
はどうかな?
できそうなことは、ボイル・シャルルの法則を使うことかな?
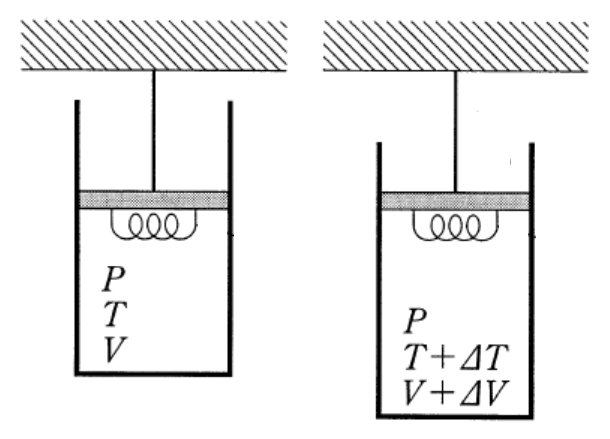
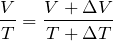
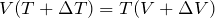
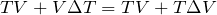
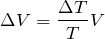

ヒーターが気体に与えた熱量
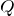
を求めるのね。
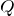
を求めるときは、熱力学第1法則というイメージが強いんだけど。
実際は他にもあるけど、確かに熱力学第1法則が多いね。
だけど、熱力学第1法則って、なかなか分かりにくいのよね。
図を描いてみると分かりやすいかな。まず、熱は入ってきている?出ている?
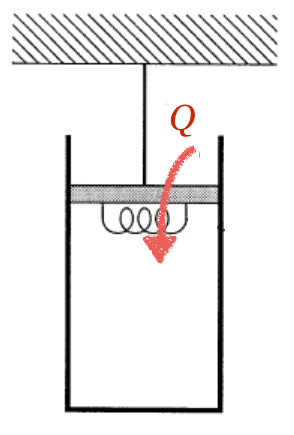
そうだね。じゃあ、仕事はどう?気体は外に仕事をしたのか、外から仕事をされたのか。
確かにそうだね。でも仕事は単純で、気体の体積が増えていれば外に仕事をしたことになるし、気体の体積が減っていれば外から仕事をされたことになるんだね。
ということは、体積が増えているから、外に仕事をしたのね。図に描くとこうかな?
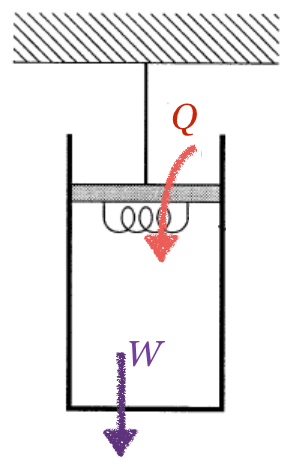
そうだね。内部エネルギーの増加量を図に描くとこうなるので、
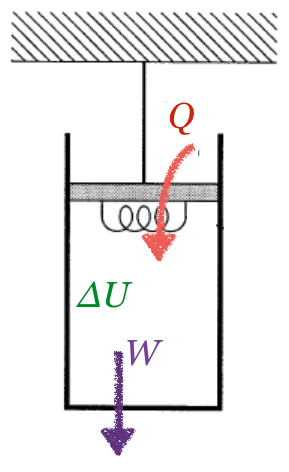
この図から、文章を作るんだ。「外から熱量
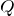
を加えた結果、外に仕事
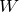
をして、内部エネルギーが
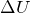
だけ増えた」と考えるんだ。
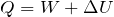
できるじゃない!そういうことだよ。あとは選択肢を見ると、
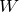
をどうにかしなきゃダメだね。
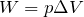
そうだね。この式の圧力
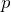
ってシリンダーの中の圧力?外部の圧力?
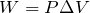
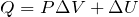


![]() だから、シリンダーを押す力はいくらになるかな?
だから、シリンダーを押す力はいくらになるかな?![]() なので、上向きの力は
なので、上向きの力は![]() ね。
ね。


![]()
![]()

![]() の式で覚えなければならない式は1つだけなんだけど、「単原子分子理想気体」の場合という条件付きで、
の式で覚えなければならない式は1つだけなんだけど、「単原子分子理想気体」の場合という条件付きで、![]()
![]() だということで、どうなるかな?
だということで、どうなるかな?![]() だけ温度が上昇しているので、
だけ温度が上昇しているので、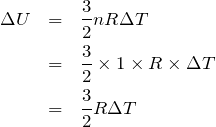
![]() はどうかな?
はどうかな?
![]()
![]()
![]()
![]()

![]() を求めるのね。
を求めるのね。![]() を求めるときは、熱力学第1法則というイメージが強いんだけど。
を求めるときは、熱力学第1法則というイメージが強いんだけど。


![]() を加えた結果、外に仕事
を加えた結果、外に仕事![]() をして、内部エネルギーが
をして、内部エネルギーが![]() だけ増えた」と考えるんだ。
だけ増えた」と考えるんだ。![]()
![]() をどうにかしなきゃダメだね。
をどうにかしなきゃダメだね。![]()
![]() ってシリンダーの中の圧力?外部の圧力?
ってシリンダーの中の圧力?外部の圧力?![]()
![]()