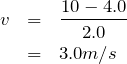■まずは図を描く
慌てちゃダメだよ。この問題はそれほど難しくはないので,使う式さえ分かれば計算ができるかもしれないけど,やっぱりまずは図を描かなきゃ。こういう問題で図を描く練習をしておかないと,ちょっと難しくなると,図も描けなくなるよ。
文章だけの問題だから,一から図を描かなきゃだめよね。図を描くのは苦手なのよ。
最初の状況は描けるでしょ。まず

軸を描いて,小球Aと小球Bの速さとその向き,質量を描こう。
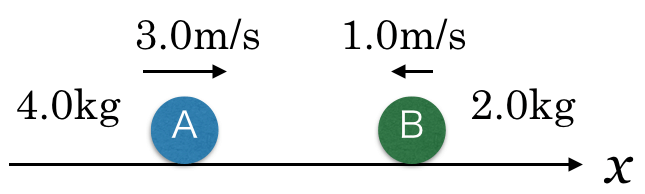
いいじゃない。小球Bの速度は負の向きなんだよね。一応確認だけど,「速さ」と「速度」の違いは分かってる?
問題文には「正の向きに速さ3.0m/s」と「速さ」となっているわね。確か,「速さ」は大きさだけを持っていて,「速度」は大きさと向きを持つんじゃなかったっけ?
だとすると,もしかして小球Bの速度は「-1.0m/s」とマイナスを付けるの?
それはどっちでもいいんだけど,僕はマイナスを付けない方がいいと思うな。
この問題のように一直線上の運動だと,向きをプラスマイナスで表すことができるけど,平面上の運動や立体的な運動だと符号で表すことはできないんだ。なので一直線上の運動であっても,基本は「向きは符号ではなく,矢印で表す」としておいた方が間違いは無くなると思うよ。
なるほどね,そうするわ。ということは,この図のままでいいわよね。この後,小球Aと小球Bは衝突するのよね。
■向きが分からなければ正にする
こんな感じかな?でも衝突後の小球Bの動きが分からないわ。
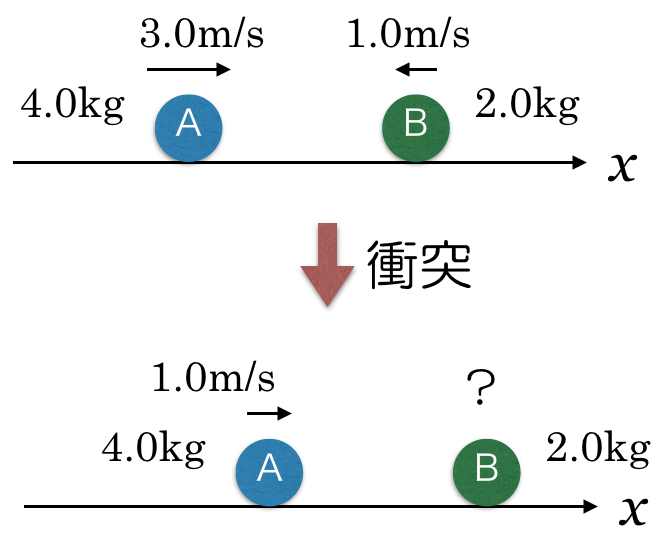
とりあえず,衝突後の小球Bの速さを

と置くわね。向きはどうしよう。
何となくだったら,

軸の正の向きかな。小球Aが衝突後も

軸の正の向きに動いているから,小球Bの進む向きが負の向きだと,また2つの小球は衝突することになるわよね。
そうだね。衝突後の小球Bの速度の向きは

軸の正の向きで正解だ。ただ実際は,向きが分からない場合,とりあえず正の向きに取っておくのが基本だから覚えておいてね。
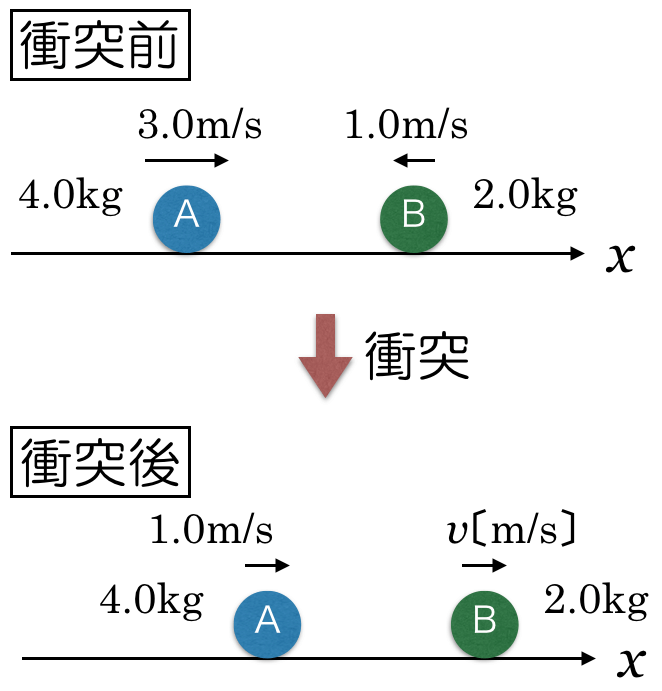
■「衝突」→「運動量保存の法則」
この図から式を立てるんだけど,2つの物体が「衝突」するときは,だいたい使う式は決まってるんだ。
「衝突」,「合体」,「分裂」などのキーワードがある場合は,「運動量保存の法則」を使うことが多いんだ。
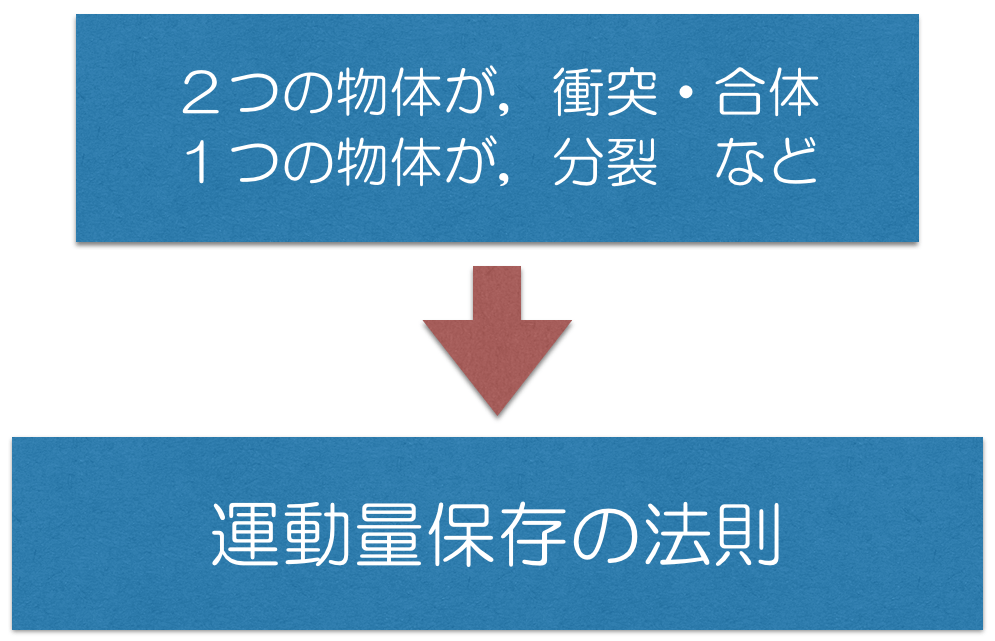
「運動量保存の法則」がどのような場合に使えるのかは,教科書などで調べてもらうとして,簡単に言うと,「衝突・合体・分裂などの前後で,運動量の総和は変化しない」というが「運動量保存の法則」だよ。
運動量って,確か
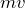
よね。
その通り。それと大切なのが「運動量はベクトル」っていうことだよ。
ということは,負の向きに運動しているときは,運動量も負になるということね。
その通りだ。それでは図を見ながら式が立てられるかな?

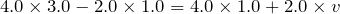
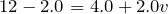
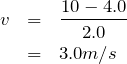

![]() 軸を描いて,小球Aと小球Bの速さとその向き,質量を描こう。
軸を描いて,小球Aと小球Bの速さとその向き,質量を描こう。

![]() と置くわね。向きはどうしよう。
と置くわね。向きはどうしよう。![]() 軸の正の向きかな。小球Aが衝突後も
軸の正の向きかな。小球Aが衝突後も![]() 軸の正の向きに動いているから,小球Bの進む向きが負の向きだと,また2つの小球は衝突することになるわよね。
軸の正の向きに動いているから,小球Bの進む向きが負の向きだと,また2つの小球は衝突することになるわよね。![]() 軸の正の向きで正解だ。ただ実際は,向きが分からない場合,とりあえず正の向きに取っておくのが基本だから覚えておいてね。
軸の正の向きで正解だ。ただ実際は,向きが分からない場合,とりあえず正の向きに取っておくのが基本だから覚えておいてね。

![]() よね。
よね。
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() 軸を描いて,小球Aと小球Bの速さとその向き,質量を描こう。
軸を描いて,小球Aと小球Bの速さとその向き,質量を描こう。

![]() と置くわね。向きはどうしよう。
と置くわね。向きはどうしよう。![]() 軸の正の向きかな。小球Aが衝突後も
軸の正の向きかな。小球Aが衝突後も![]() 軸の正の向きに動いているから,小球Bの進む向きが負の向きだと,また2つの小球は衝突することになるわよね。
軸の正の向きに動いているから,小球Bの進む向きが負の向きだと,また2つの小球は衝突することになるわよね。![]() 軸の正の向きで正解だ。ただ実際は,向きが分からない場合,とりあえず正の向きに取っておくのが基本だから覚えておいてね。
軸の正の向きで正解だ。ただ実際は,向きが分からない場合,とりあえず正の向きに取っておくのが基本だから覚えておいてね。

![]() よね。
よね。
![]()
![]()