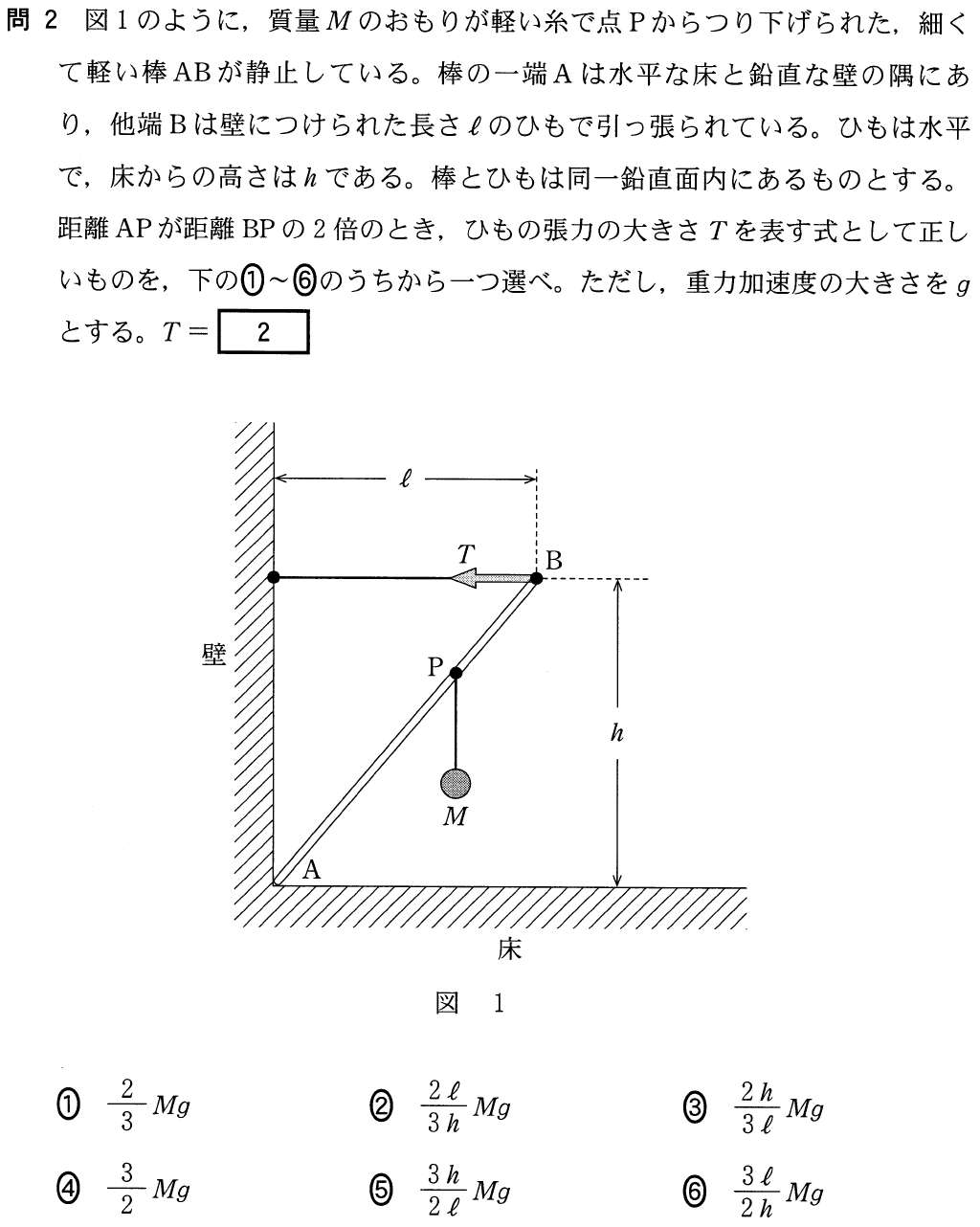
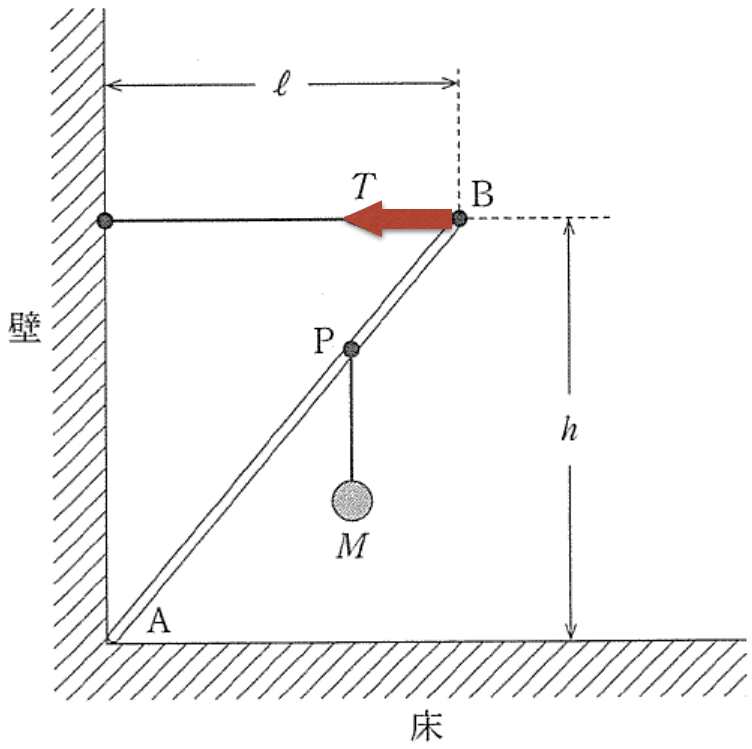
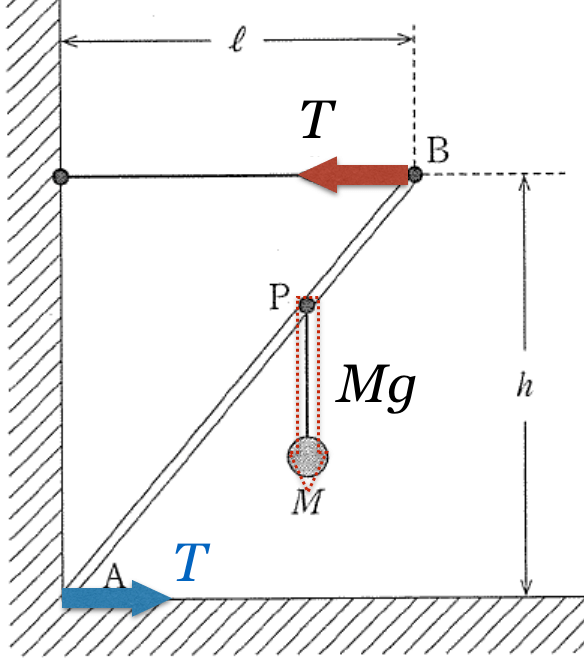
■まずは力の矢印を描く
棒が静止している問題ね。見たことがある気がするわ。
棒が出てくる問題って，だいたい「力のモーメントのつりあい」の式を使うわよね。
そうなの。じゃあ仕方ないので，棒にはたらく力の矢印を描くわ。
力の矢印は，
１．重力
２．くっついているものから受ける力
の順で考えるといいよ。
それじゃあまずは，重力ね。棒の真ん中に
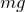
でいいわよね？
よくないよ。問題文に棒の質量が書かれていないでしょ。さらに「軽い棒」とあるでしょ。
そうか，「軽い」というのは質量が無視できるということだったわね。
それじゃあ重力は描かないので，次はくっついているものから受ける力ね。棒の端Bはひもで引っ張られていて，その大きさは
とすでに描かれているわね。敢えて矢印を重ねて強調しておくわ。
いいね。その
を求めるんだね。
■点Pにはたらくのは，糸が引く力
あとは点Pにおもりがぶら下がっているので，おもりから力を受けるのね。
この場合は確かにその考え方でも大丈夫だね。だけど，本当は棒にくっついているのは糸だから，棒は糸から力を受けるんだ。図には
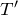
と描いておくよ。
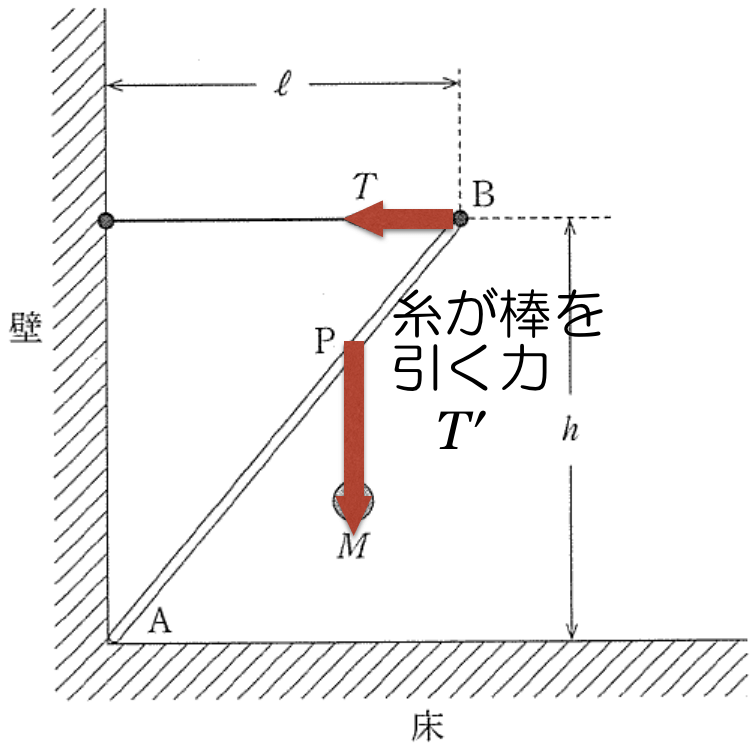
逆に，棒はおもりとはくっついていないので，おもりからは力を受けないんだよ。
おもりが糸を引っ張って，糸が棒を引っ張ってるっていうイメージだね。
「おもりは棒にくっついていないから，棒はおもりから力を受けない」という非常にシンプルな考え方なんだけどな。そこが物理のいいところだけど，苦手な人にとっては嫌なんだよね。
ちゃんとやると，おもりにはたらく力を描く必要があるんだ。描けるかな？
おもりにはたらくのは，重力
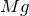
と，糸がおもりを引く力ね。糸がおもりを引く力は
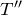
でいい？
糸はどこでも張力の大きさは同じなので，
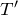
と描いていいんだよ。さっき描いた「糸が棒を引く力」と同じ大きさね。
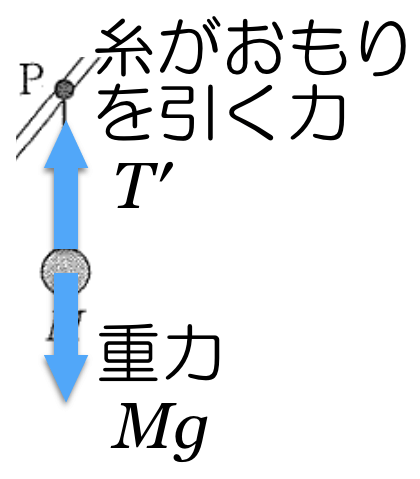
おもりは静止しているので，力のつりあいの式を立てることができで，鉛直上向きを正とすると，こうなるよ。
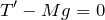
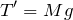
ということは，糸が棒を引く力も
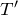
だから，結局はこういうことね。
そうなんだよ。なので，結局はおもりが棒を引っ張っていると考えてもOKなんだ。でも今のような考え方の結果だということは理解しておいたほうがいいね。
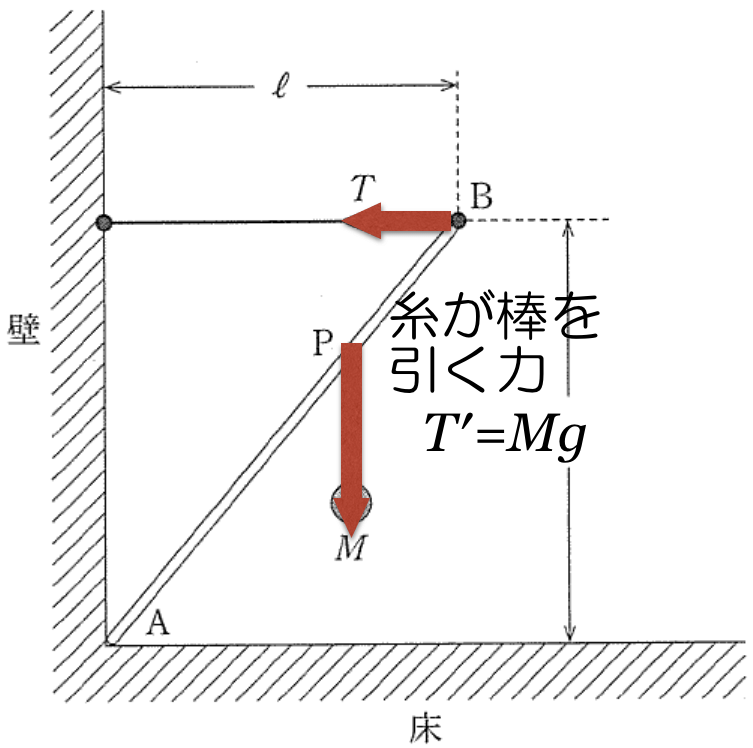
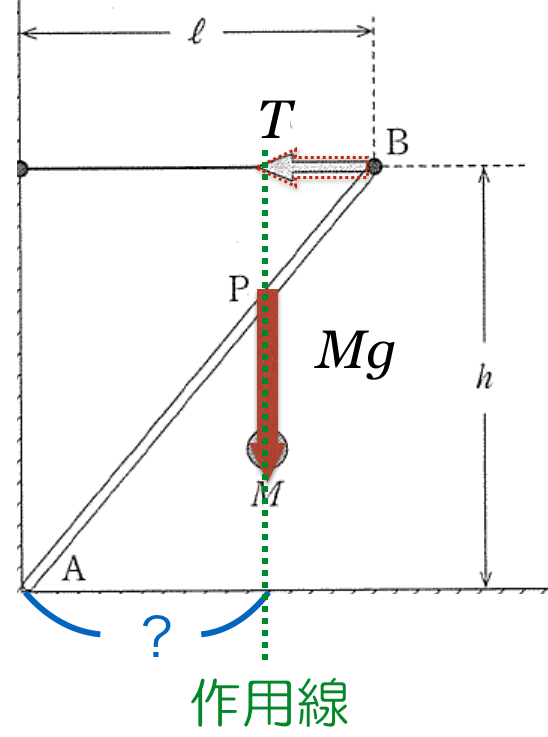
今のところは分かったわ。あと棒にはたらくのは，端Aが壁と床から受ける力かな？ちょうど角なので，力の向きが分からないわ。
実際は棒が壁と床から受ける力の大きさや向きは分かるんだけど，今は分からなくてもこの問題は解けるんだ。
■力のモーメントの定義
この問題は「力のモーメントのつりあい」の式を立てて，計算するんだけど，点Aのまわりの力のモーメントのつりあいの式を立てれば，点Aにはたらいている力は結果的に式には出てこないんだ。
「点Aのまわりの力のモーメント」は，「力×点Aから力の作用線までの長さ」で求めることができるんだ。
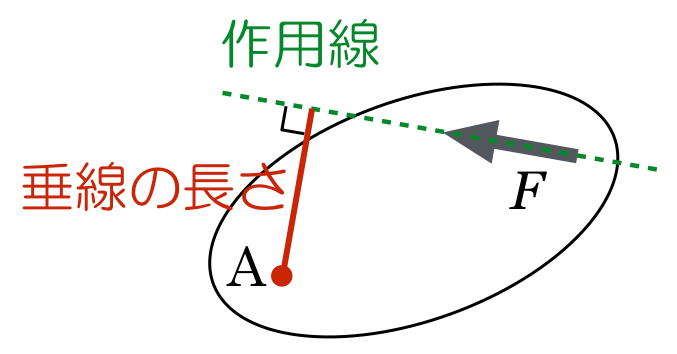
ということは，点Aから力の作用線までの長さが0だったら，力のモーメントも0ということね。だから点Aにはたらく力は考えなくていいのね。
そういうことだね。それから，力のモーメントには正負があるんだ。点Aを固定したと考えて，力によって反時計回りに回転する場合を正，時計回りに回転する場合を負とするんだ。
この問題の場合，棒は静止しているから回転しないわよね。
そうなんだよ。他の問題でも棒は回転しないんだ。反時計回りに回転させようとする力と，時計回りに回転させようとする力がつりあっているから回転しないんだ。棒は回転しないけど，１つひとつの力について，回転させる向きを考えるんだ。
なるほど，分かったわ。１つひとつの力について考えるのね。それじゃあまず点Bにはたらいている
から考えましょうか。
その時に大切なのが，もう一つの力，点Pにはたらいている
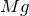
は考えないんだよ。それと，点Aは固定されているんだけど，点Aを中心に棒は自由に回転できると考えるんだ。
点Aは固定されていて，
だけを考えると，棒は反時計回りに回転するわね。
そうだね。そうすると，
による力のモーメントの符号は正ね。あとは力×点Aから作用線までの長さだ。
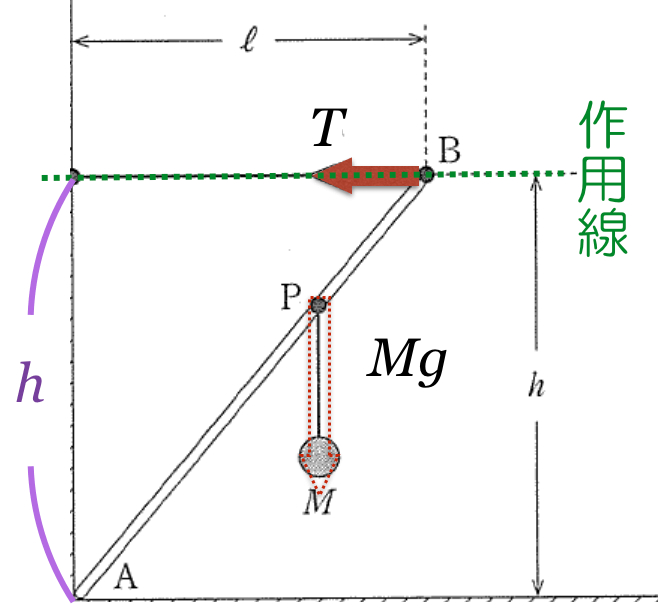
そうだね。作用線は，その力の矢印を含む直線なので，その作用線に点Aから下ろした垂線の長さ
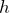
を使えばいいね。
まず，
による点Aのまわりの力のモーメントは，
ということですか？
いいね。それじゃあ
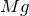
の方も力のモーメントが分かるかな？
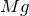
の作用線までの長さが難しいわ。
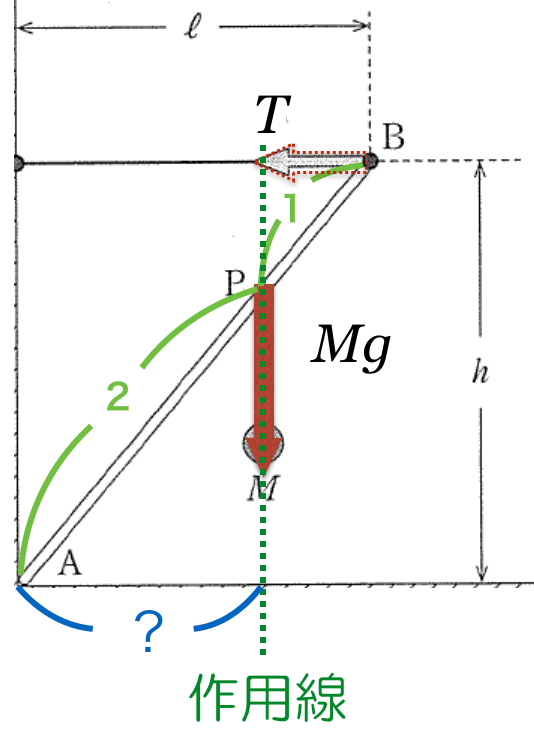
そうか，ということは，こう考えれば
ですね。
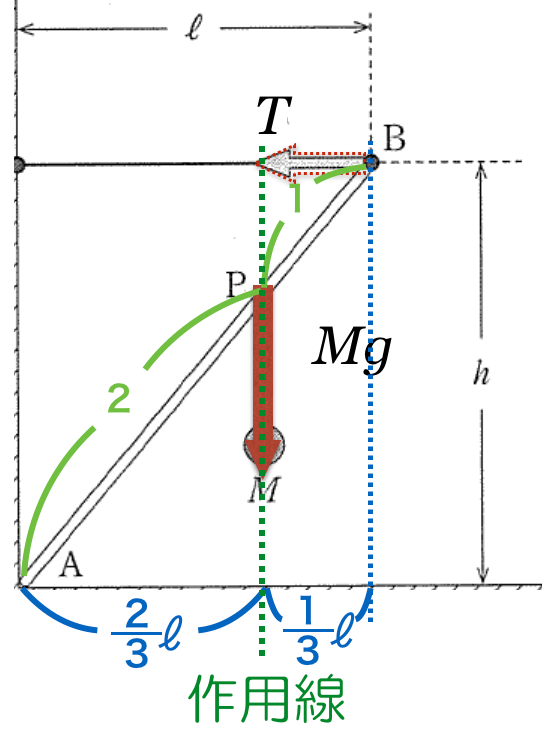
では，
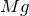による点Aのまわりの力のモーメントは，時計回りになるのでマイナスが付きますね。
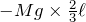
その通りだよ。点Aにはたらいている力は考えなくていいので，この２つの力のモーメントがつりあっているんだ。
■力のモーメントのつりあい
この２つの力のモーメントの和=0という式を立てればいいんだ。
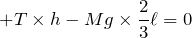
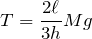
■点Aにはたらく力
さっき，点Aにはたらく力は分かるって言ってたわよね。
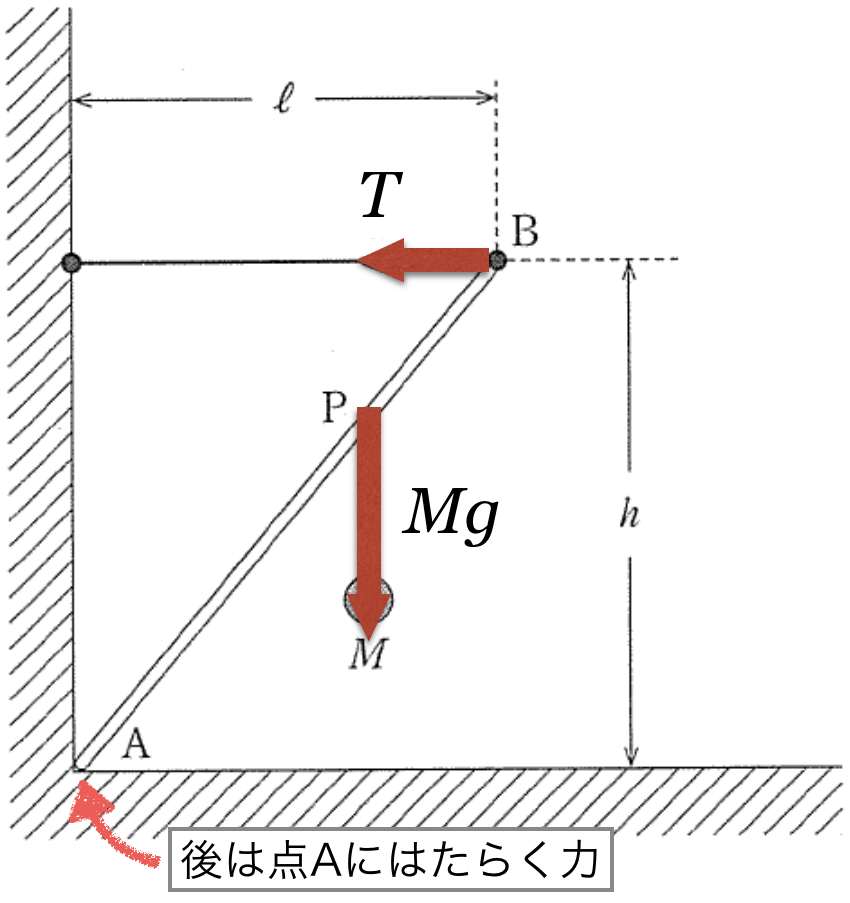
棒にはたらいている力は，点Bにはたらくひもが引く力
と，点Pにはたらく糸の張力（＝おもりの重力
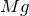
）と，点Aにはたらく力の３力だよね。
さっきの計算結果，
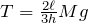
だから，この図で考えると
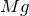
よりも
の方が小さそうだよね。
なるほど。確かに図では
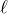
よりも
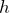
の方が大きくて，式では分母の方が大きくなりそうだから，
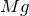
よりも
の方が小さそうなのね。
さらに点Aにはたらく力も加えた，３つの力がつりあっているんだよね。
水平方向と鉛直方向に分けて考えてみよう。図では水平方向にはたらく力は左向きの
しかないから，点Aにはそれとつりあうような水平方向右向きで大きさが
の力がはたらいているはずなんだ。
そうか。すでに左向きの力があるから，力がつりあうためには右向きの力が必要なのね。
同様に，鉛直方向の力のつりあいを考えてみるとどうなるかな？
図には鉛直下向きの
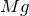
しかないから，点Aには鉛直上向きで大きさが
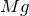
の力がはたらいているはずなのね。
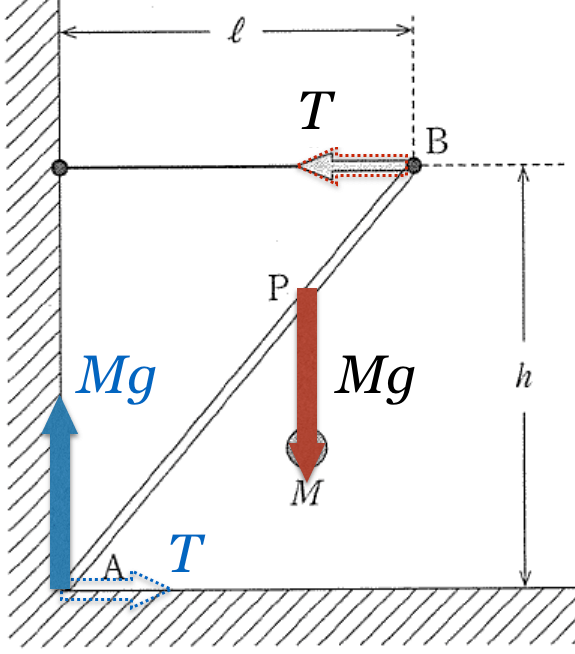
ということは，点Aにはたらいている力は，水平右向きの
と，鉛直上向きの
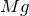
の合力ということね。
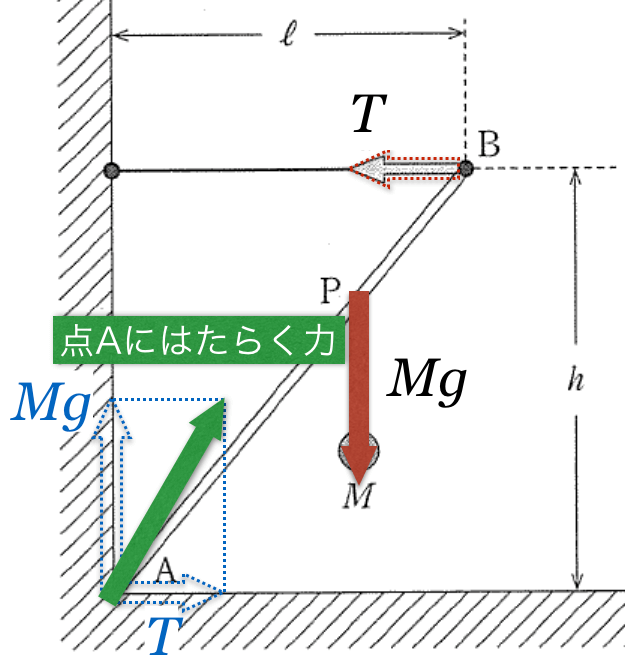
■点Aにはたらく力の向き
そういうことなんだよ。ついでに，向きについても考えておこうか。点Aにはたらく力は，右上向きなんだけど，どこに向かうと思う？
どこに向かう？って言われても，右上向きとしか分からないわ。もっと具体的に向きが分かるの？
分かるんだよ。明確に「ここの点の方を向く」っていう点があるんだ。
実は，点Bにはたらく
の作用線と，点Pにはたらく
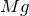
の採用線の交点に向かう向きが，点Aにはたらく力の向きなんだ。
棒のような剛体に，互いに平行ではない３力がはたらいていてつりあっている場合，３力の作用線は１点で交わるんだ。この性質を知っていると役に立つよ。
