動画解説をYouTubeにUPしました。動画での解説と、このサイトでの解説を少し変えましたので、ぜひどちらも参考にしてください。
■必要な情報を文字で置けるかが勝負
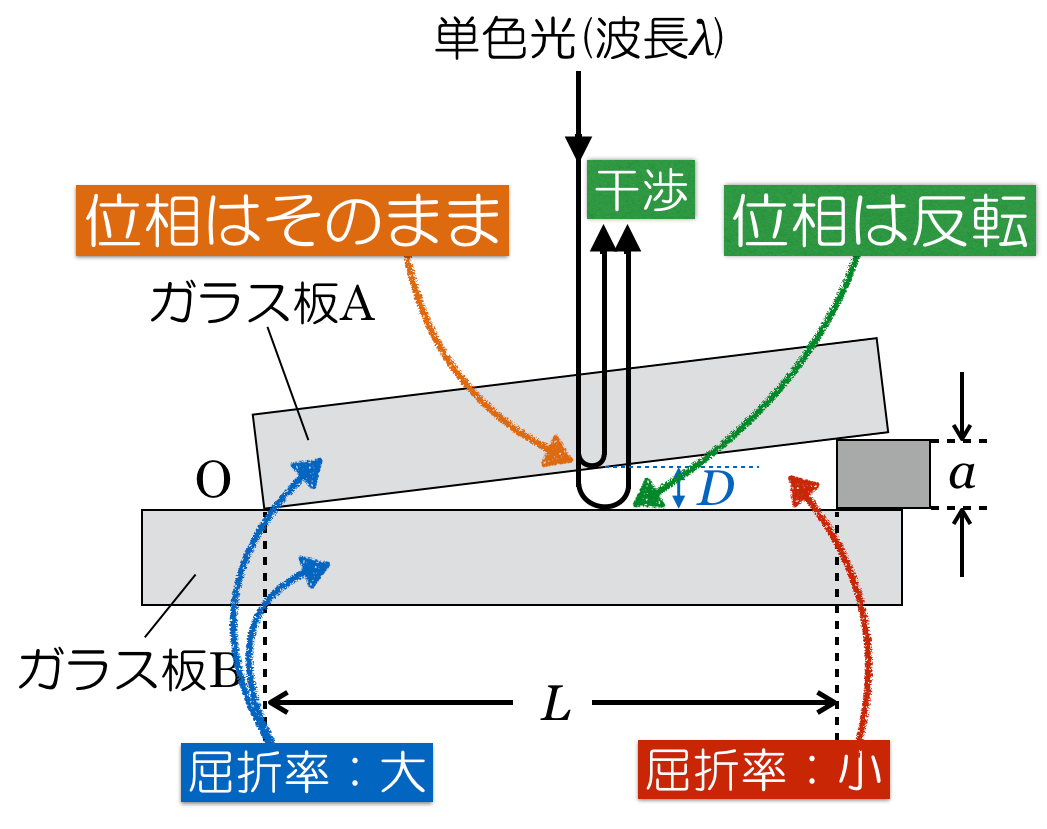
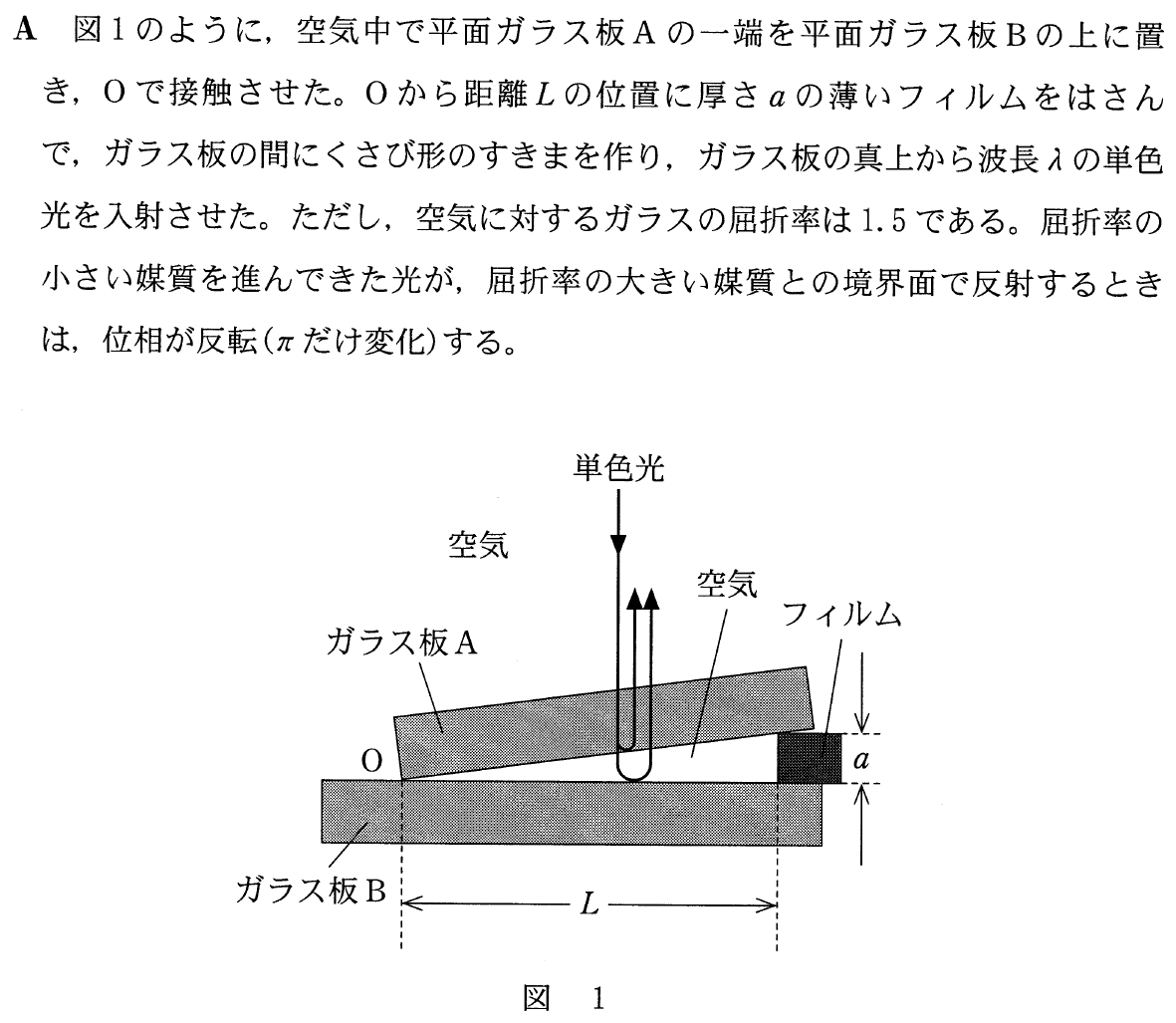
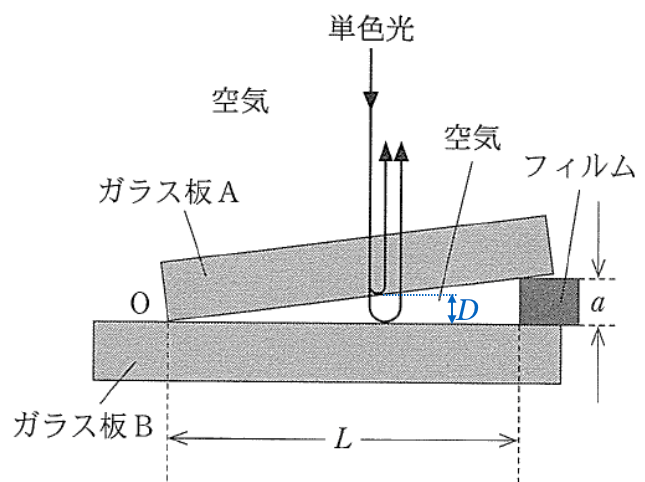
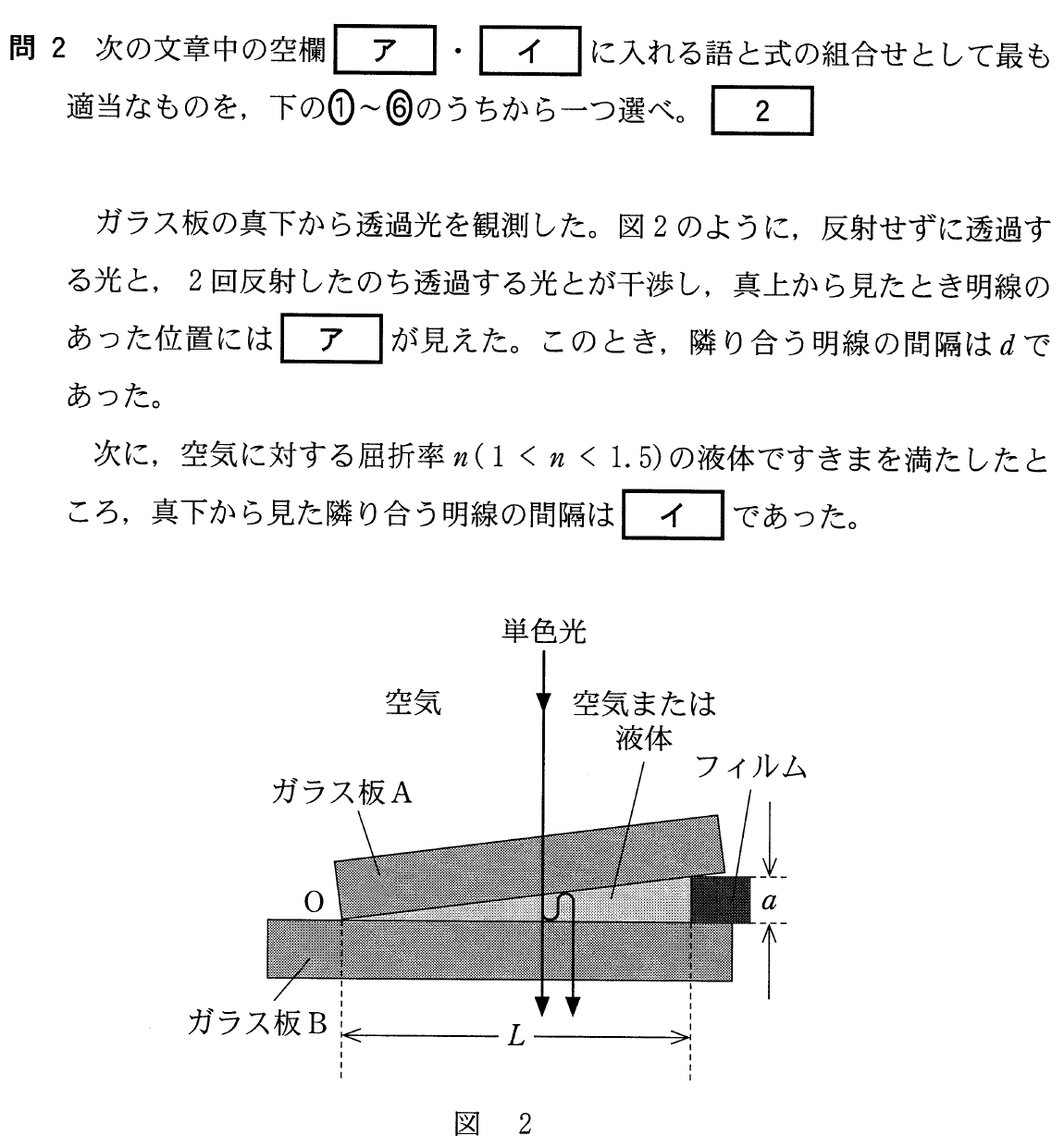
くさび形空気層」っていうのが,図の真ん中の直角三角形の部分ね。
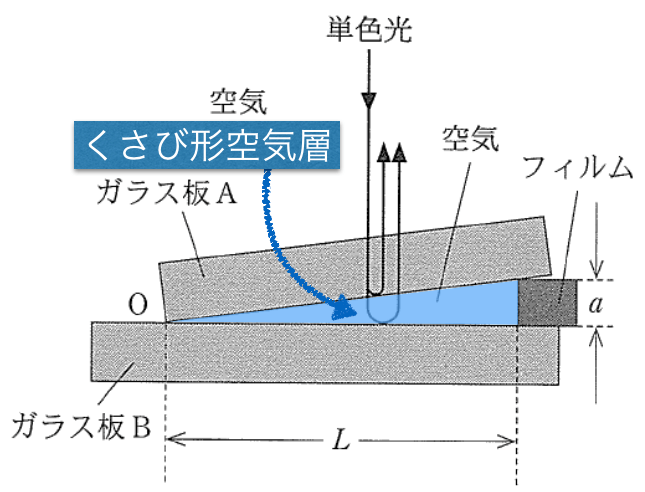
この部分は実際はすごく薄いんだよ。そして,問題文にある通り,真上から見ると,明暗の縞模様になっていて,隣り合う明線の間隔が
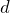
なんだね。
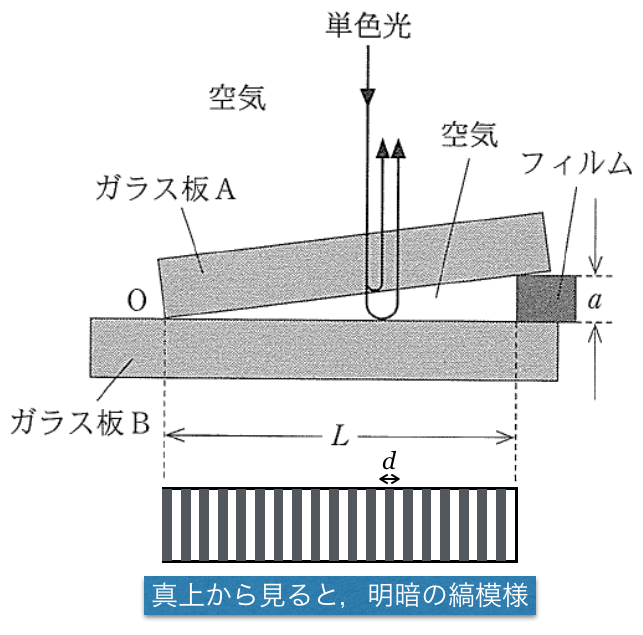
そこまでは見たことあるので分かるんだけど,明線の間隔
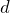
をどうやって求めればいいか,分からないわ。
確かにこのくさび形空気層の問題はよくあるんだけど,いきなり明線の間隔を求めるのはなかなか厳しいね。自分でいろいろと決めなきゃダメなんだ。まずは順番に考えていこうか。
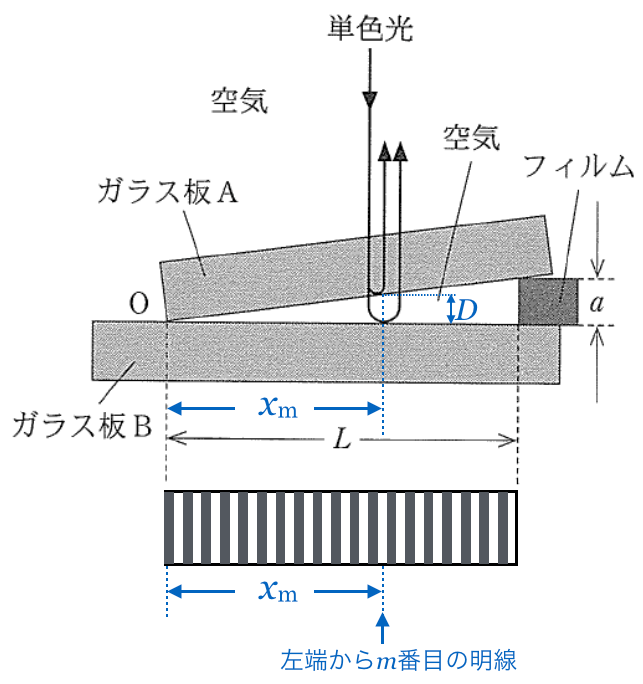
まず,左端から
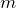
番目の明線までの長さを
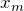
として,その位置での空気層の厚さを
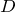
とするよ。
図の通りということね。ただ,この
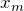
や
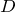
は自分で決めなきゃダメなの?思いつかないわ。
そうなんだよね。文字は違うかもしれないけど,教科書には必ず出ている計算の流れなので,やっぱり自分で決めれるようにしておいたほうがいいね。
逆に言うと,「くさび形空気層の干渉の公式」みたいな式を覚えるより,この流れを理解するほうがずっといいよ。
■明線の条件,暗線の条件
空気層の厚さが
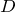
で明るくなる条件を求めよう。
図のように空気層の上面で反射した光と,下面で反射した光が干渉するんだよね。

空気層の下面で反射する光の方が,
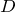
の往復分,つまり
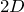
だけ距離が長くなっているのよね。
そう,経路差は
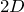
だ。それで,さっきの干渉の基本の式なんだけど,反射があるときは注意が必要なんだよね。
■「反射」があるときは注意!
反射があるときは位相が反転するとか,反転しないとかを考えなきゃダメなのね。
そうだね。反転が1回あると,強めあう条件と弱め合う条件が逆になるんだ。そして反転が2回あると元に戻るんだよね。

問題文に「屈折率の小さい媒質を進んできた光が,屈折率の大きい媒質との境界面で反射するときは,位相が反転(
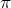
だけ変化)する。」とあるね。

「空気に対するガラスの屈折率は1.5である。」と問題文にあるわ。
普通は「空気の屈折率が1,ガラスの屈折率が1.5」とするんだけどね。大切なのは,ガラスのほうが屈折率が大きいということだね。
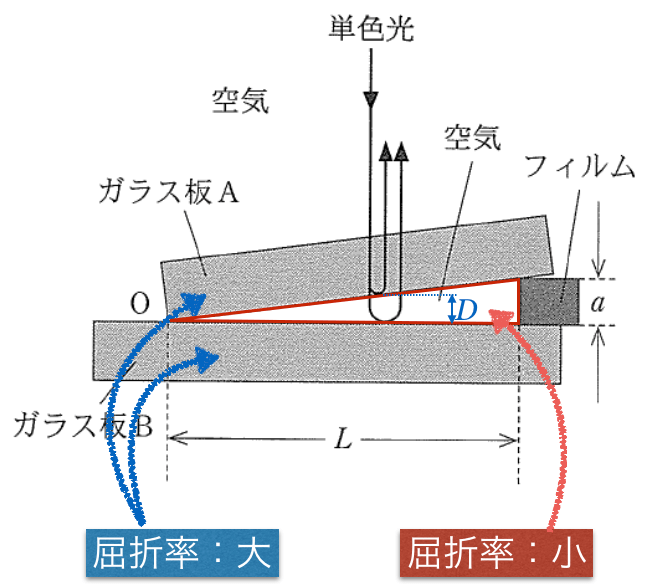
そうすると,空気層の上面で反射する光は位相が反転しないけど,空気層の下面で反射する光は位相が反転するのね。
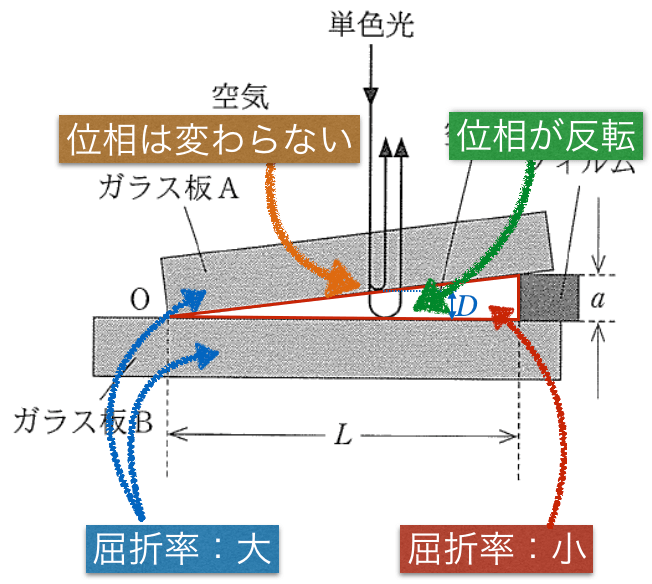
ということは,位相が反転するのは1カ所なので,干渉によって強めあう条件と弱め合う条件が入れ替わるのね。今は明線の位置について考えていたので,強めあう条件を書くと,
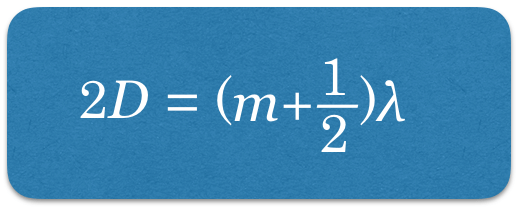
そこまではいいね。次は
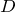
を求めるんだ。
■比を使って関係を表す
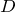
を求めるのは,どうすればいいの?
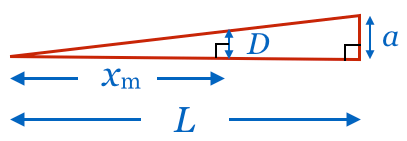
なるほど,こうやって描いてみるとなんとなく分かりますね。こんな式になりますね。
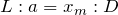
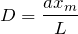
いいね。これをさっきの条件式に入れて計算してみるよ。
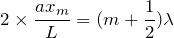
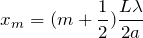
なるほど。これで
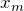
が分かったのね。でも求めたいのは明線の間隔
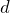
なのよね。
■dとxmの関係
明線の間隔
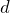
はどこでも等間隔なので,こう表すことができるよ。
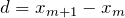
なるほど,数学の漸化式みたいな考え方ね。あとは,
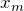
の式を使えばいいのね。
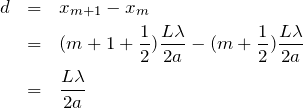
■やっぱり「反射」に注目しよう
問題としては,ときどきあるかな。ポイントは,位相が反転する反射が何回あるかを数えることだよ。干渉する2つの光の経路は,図を見れば分かるよね。
1つは1度も反射せずに,まっすぐ透過する光ね。もう1つは,空気層の下面で反射して,次に上面で2回目の反射をして真下に抜けてくる光ね。位相の反転はこんな感じね。
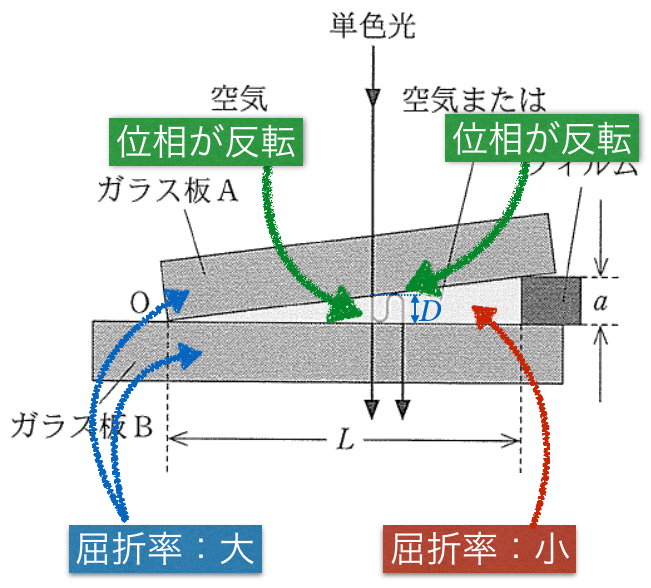
ということは,位相の反転が2回起こるということだね。干渉の条件はどうなるかな?
位相の反転が2回ということは,反転が無い場合と同じだから,こうね。

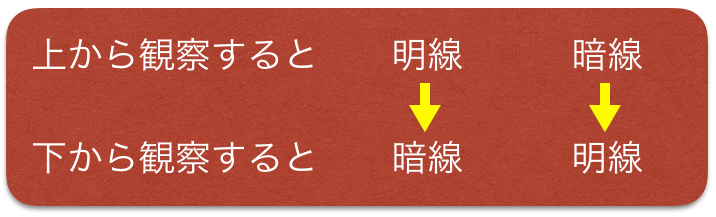
そうだね。これって,さっきの真上から観察したときと逆になっているよね。

強めあう条件と,弱め合う条件が逆になるんだから,上から見たときに明線だと,同じ位置でしたから見たときは暗線になるということだね。
■屈折率の大小関係を確認
そうだね。次は,空気層のところを屈折率
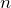
の液体で満たしたときだね。
まず,位相が反転する反射の数が変わるかもしれないね。屈折率の大小関係で位相が反転するか,しないかが決まるからね。
液体の空気に対する屈折率
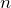
の大きさ
は,
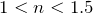
となっているわね。ということは,液体の屈折率はガラスよりも小さいということね。
ということは,屈折率がガラスより小さいというのは空気と同じなので,位相の反転も空気と同じね。
■屈折率が異なると波長が変わる
それじゃあ,液体を満たしたことで何も変わらないの?
いや,変わるものがあるんだ。光の波長が変わるんだよ。
そう。真空中の光の波長を
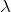
とすると,屈折率
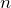
の媒質中の光の波長
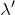
は,

この問題では空気中の波長が
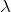
で,空気に対する液体の屈折率が
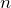
だけど,いいの?
微妙に違うよね。ちゃんと説明するとちょとややこしいけど,全く同じ関係なので,そのままこの波長の関係を使って大丈夫だよ。
そうなのね。今求めたいのは,真下から見たときの明線の間隔だけど,どうすればいい?
■明線の間隔と暗線の間隔は同じ
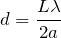
確かに明線と暗線は逆になるんだけど,明線でも暗線でも間隔は同じだよね。
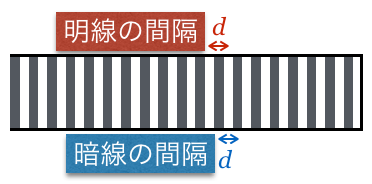
この明線の間隔の式を見ると,液体を入れることによって変わる
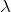
が入っているね。
この
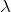
を変えればいいのね。液体を満たしたときの明線の間隔を
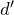
とすると,
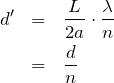
つまり空欄イに入るのは

ね。



![]() なんだね。
なんだね。
![]() をどうやって求めればいいか,分からないわ。
をどうやって求めればいいか,分からないわ。
![]() 番目の明線までの長さを
番目の明線までの長さを![]() として,その位置での空気層の厚さを
として,その位置での空気層の厚さを![]() とするよ。
とするよ。![]() や
や![]() は自分で決めなきゃダメなの?思いつかないわ。
は自分で決めなきゃダメなの?思いつかないわ。![]() で明るくなる条件を求めよう。
で明るくなる条件を求めよう。

![]() の往復分,つまり
の往復分,つまり![]() だけ距離が長くなっているのよね。
だけ距離が長くなっているのよね。![]() だ。それで,さっきの干渉の基本の式なんだけど,反射があるときは注意が必要なんだよね。
だ。それで,さっきの干渉の基本の式なんだけど,反射があるときは注意が必要なんだよね。
![]() だけ変化)する。」とあるね。
だけ変化)する。」とあるね。


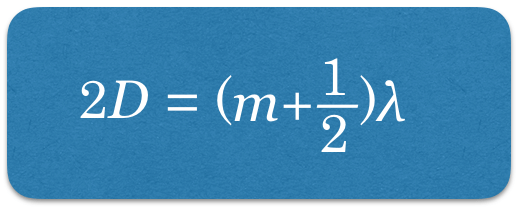
![]() を求めるんだ。
を求めるんだ。![]() を求めるのは,どうすればいいの?
を求めるのは,どうすればいいの?
![]()
![]()
![]()
![]()
![]() が分かったのね。でも求めたいのは明線の間隔
が分かったのね。でも求めたいのは明線の間隔![]() なのよね。
なのよね。![]() はどこでも等間隔なので,こう表すことができるよ。
はどこでも等間隔なので,こう表すことができるよ。![]()
![]() の式を使えばいいのね。
の式を使えばいいのね。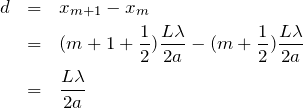






![]() の液体で満たしたときだね。
の液体で満たしたときだね。![]() の大きさは,
の大きさは,![]()
![]() とすると,屈折率
とすると,屈折率![]() の媒質中の光の波長
の媒質中の光の波長![]() は,
は,
![]() で,空気に対する液体の屈折率が
で,空気に対する液体の屈折率が![]() だけど,いいの?
だけど,いいの?![]()

![]() が入っているね。
が入っているね。![]() を変えればいいのね。液体を満たしたときの明線の間隔を
を変えればいいのね。液体を満たしたときの明線の間隔を![]() とすると,
とすると,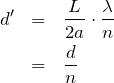
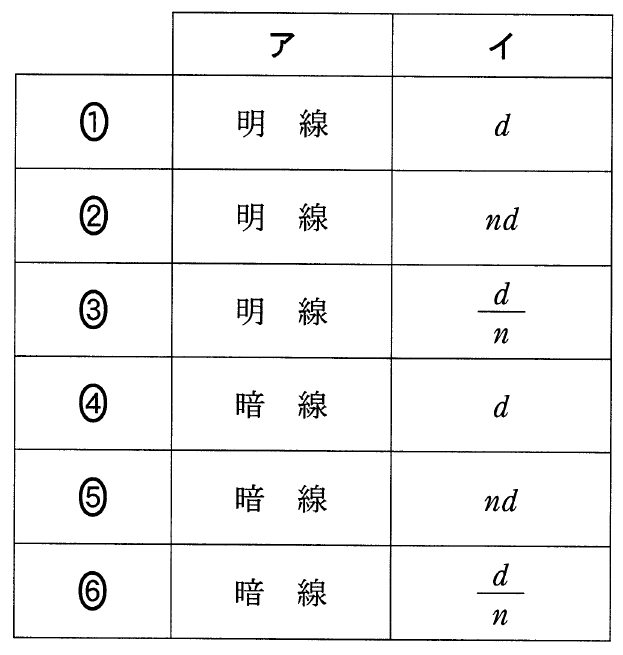
![]() ね。
ね。