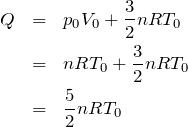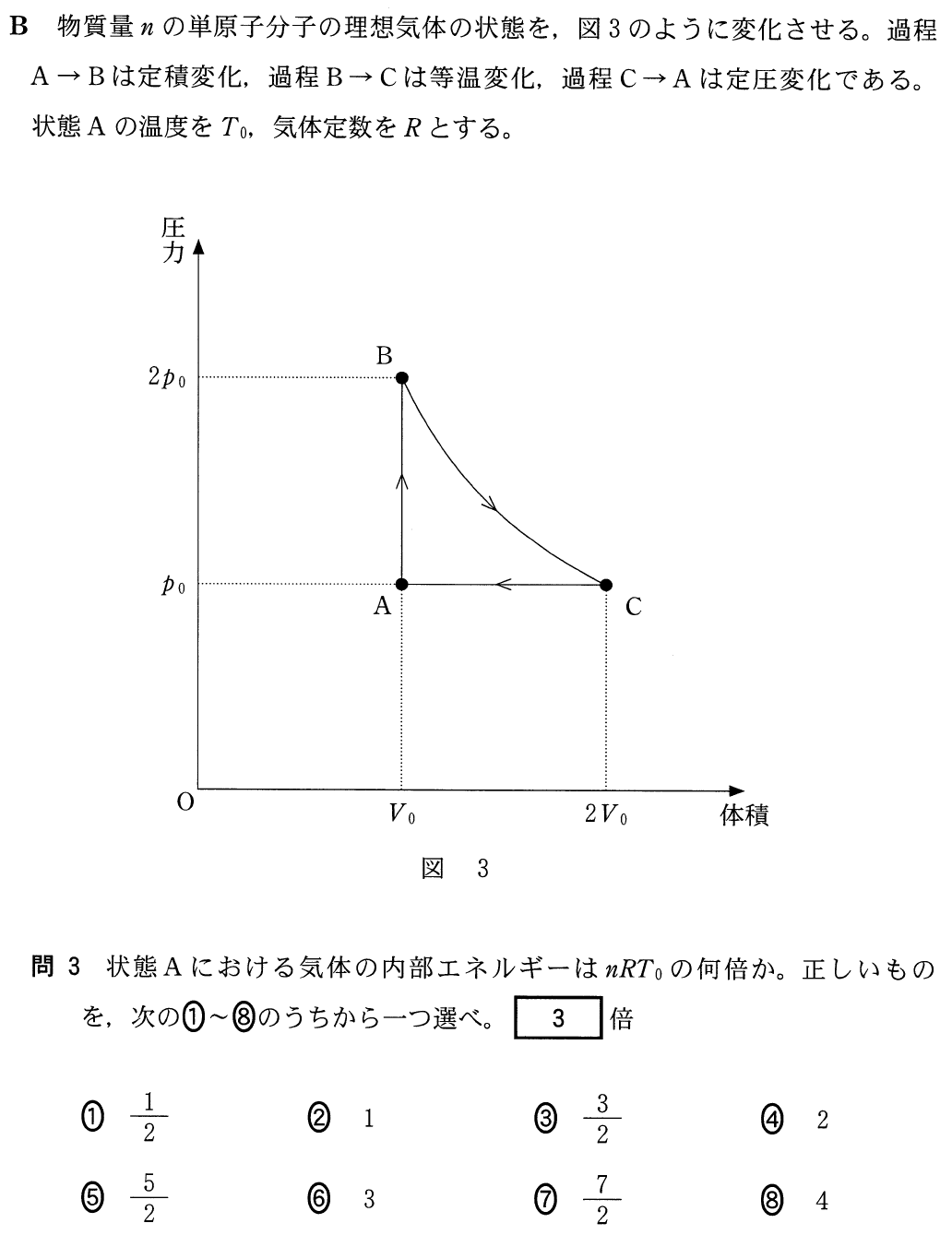
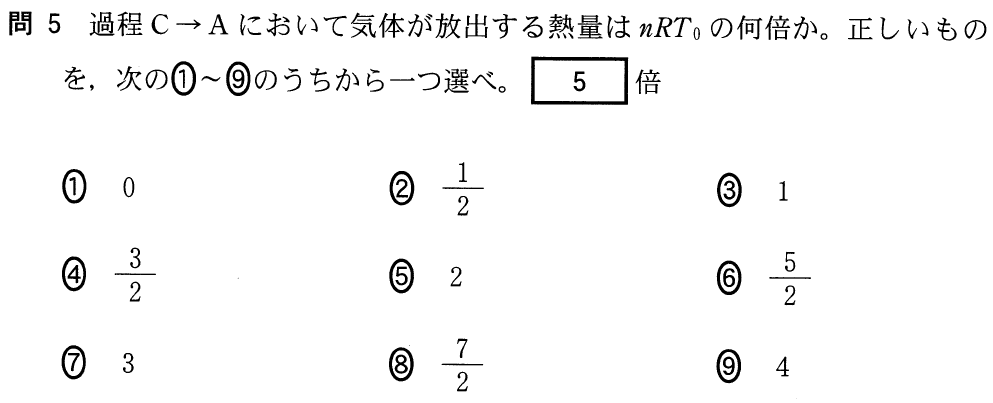
■問題文から「単原子分子」を探せ
最初に内部エネルギーを求める問題ね。どうすればいいの?
内部エネルギーについては,覚えておかなければならない重要なポイントが有るんだ。キーワードは「単原子分子」だよ。
正確には「単原子分子理想気体」なんだけど,「理想気体とはみなさい」という場合はほとんど無いので,大切なのは「単原子分子」であるかどうかなんだ。まずは問題文に「単原子分子」という言葉を探そう。
この問題ではいきなり「単原子分子」と書いてあるわ。
そうだね。もちろん「理想気体」とも書いてある。その場合,内部エネルギーが分かるんだ。

この式が使えるのね。問題文には物質量
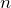
,状態Aの温度
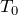
,気体定数
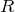
とあるので,そのまま入れればいいの?
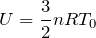

■p-Vグラフからボイル・シャルルの法則へ
他に情報はないよね。分かりやすいように情報をまとめておこうか。
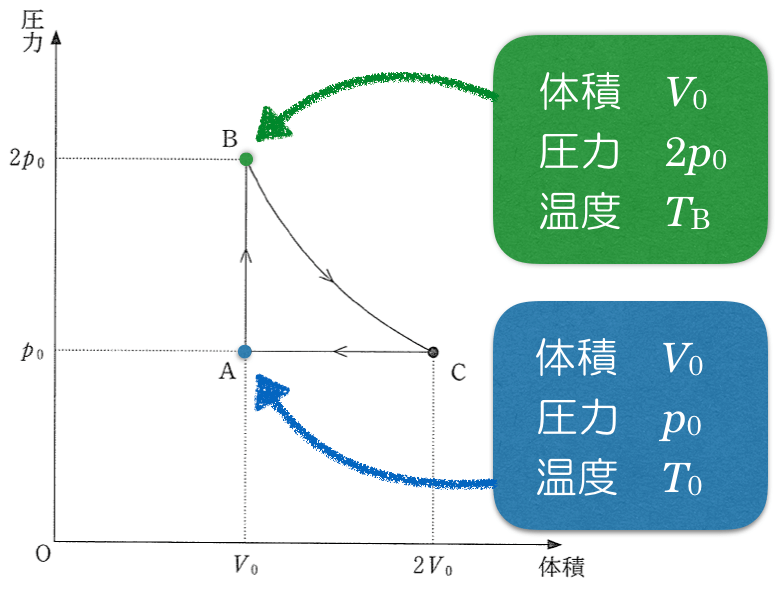
求めたい状態Bの温度を
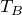
としたのね。
体積,圧力,温度の関係があるということは,「ボイル・シャルルの法則」かな?
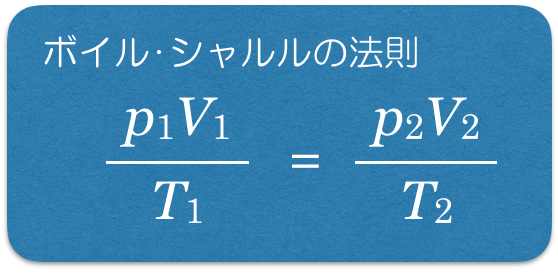
状態A=状態B
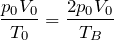
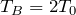
つまり,状態Bの温度は
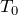
の2倍ね。
■熱力学第一法則は式と矢印の向きが大切
この分野で熱量を求める問題の場合,まず考えるのは「熱力学第一法則」だね。
確かに,熱が入ったのか出たのか,仕事をしたのかされたのか,内部エネルギーが増加したのか減少したのか,それぞれいろいろなパターンがあるからね。ポイントは,式と矢印の向きを一緒に覚えることだよ。
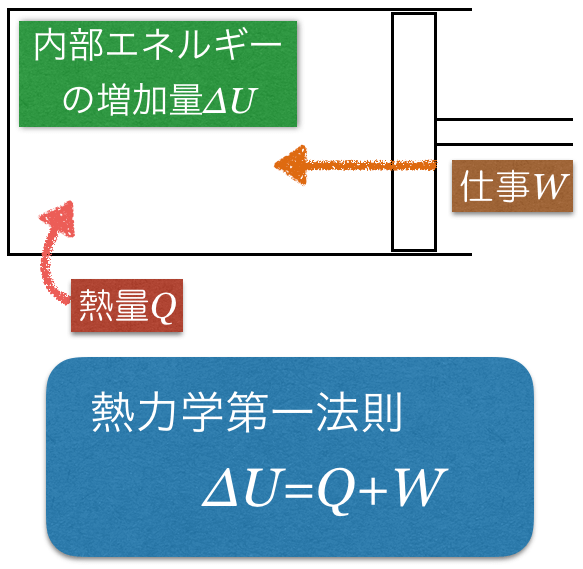
矢印の向きを考えると,気体に熱が加えられて,気体が外から仕事をされたら,内部エネルギーがその分だけ増加するっていうことね。
そのように読み取れたら完璧だよ。あとは問題文を読んで,矢印の向きが逆だと,式にマイナスを付ければいいね。
■熱量の正負
まず,問題文には「放出する熱量」とあるわ。矢印の向きで考えると,さっきの図と逆ね。
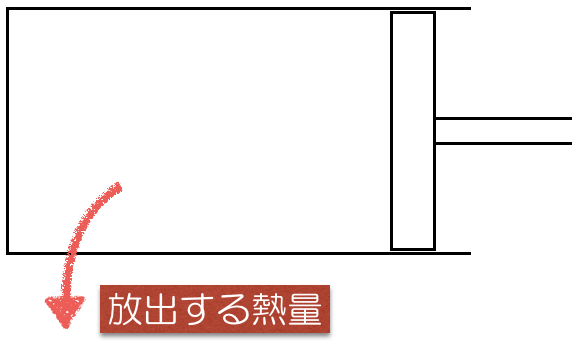
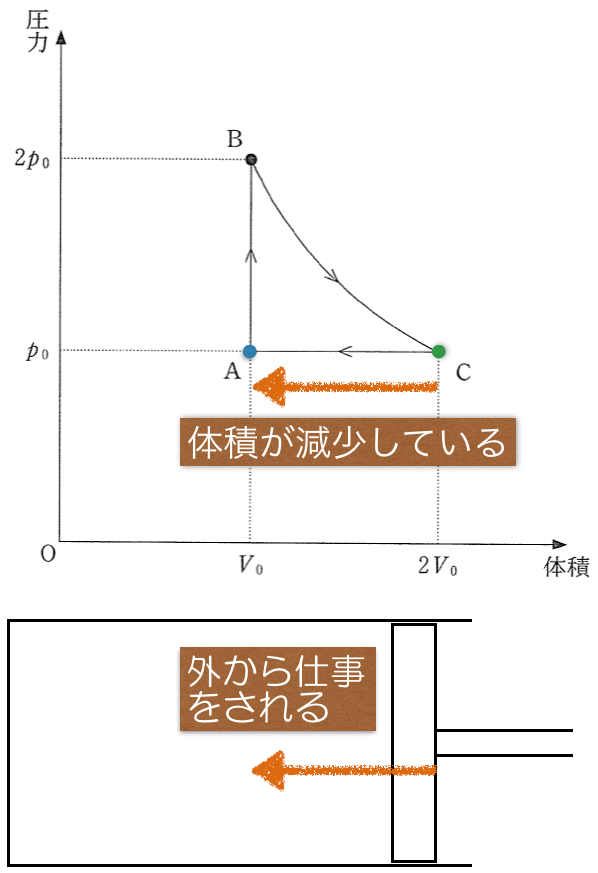
そうだね。ということは,
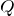
にはマイナスが付くね。仕事の正負は問題文にはないので,グラフで考えるよ。
■仕事の正負
過程C→Aを考えるので,体積は減少しているわね。つまり,仕事の矢印の向きはさっきの図と同じね。
仕事の符号はそのままでいいということだね。次は仕事の大きさを求めるんだけど,仕事を求めるときは,「定圧変化」であるかどうかが大切なんだ。

「過程C→Aは定圧変化」と問題文にあるし,グラフからもその圧力は
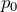
で一定と読み取れるわ。
そうだね。なので過程C→Aで気体が外からされた仕事はこうなるよ。
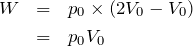
■内部エネルギーの増加量
内部エネルギーの増加量は,単原子分子理想気体の場合は,
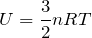
を変形すればいいんだ。


があるので,温度がわからなきゃダメね。Aの温度は
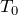
でいいとして,Cの温度はボイル・シャルルの法則で求めるの?
そんなことしなくても,「過程B→Cは等温変化」って問題に書いてあるでしょ。
そうか,ということはBの温度はさっき求めた
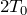
だから,Cの温度も
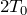
ね。
温度はわかったけど,

はどっちの温度からどっちの温度を引けばいいの?
「変化量」とか「増加量」という場合は,「あとの量からまえの量を引く」んだ。

ということは,過程C→Aを考えているんだから,Aの温度からCの温度を引くね。
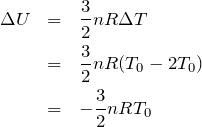
いいんだよ。増加量がマイナス,ということは内部エネルギーは減少したっていうことだよね。つまり温度が下がったということだ。それでは熱力学第一法則を考えてみるよ。
いろいろあったので,まとめてみるわ。まずは熱力学第一法則の式の
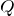
がマイナスになるので,
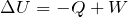
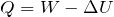
ここに,求めた
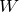
と
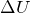
を入れると,
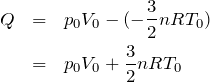
でも求めたいのは,この
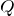
が
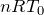
の何倍か,ということよ。
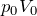
が邪魔だわ。
■理想気体の状態方程式
そうだね。でも気が付かないかな。
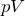
が使えなくて,
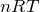
で表したいんだよ。

この理想気体の状態方程式は,グラフのA,B,Cのどの点でも成り立つんだ。
もちろん,どこでもいいんだ。一番シンプル式が立てられそうなのはAだよね。Aで式を立ててみると,
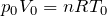
そうだね。話を戻すと
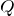
はどうなるかな?
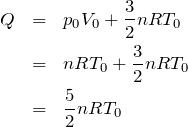


![]() ,状態Aの温度
,状態Aの温度![]() ,気体定数
,気体定数![]() とあるので,そのまま入れればいいの?
とあるので,そのまま入れればいいの?![]()


![]() としたのね。
としたのね。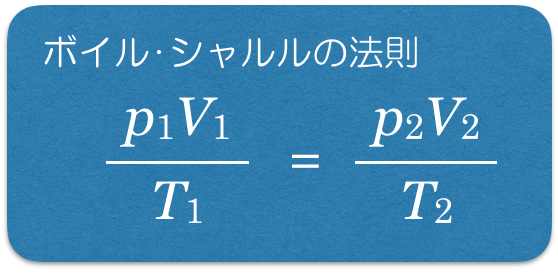
![]()
![]()
![]() の2倍ね。
の2倍ね。


![]() にはマイナスが付くね。仕事の正負は問題文にはないので,グラフで考えるよ。
にはマイナスが付くね。仕事の正負は問題文にはないので,グラフで考えるよ。

![]() で一定と読み取れるわ。
で一定と読み取れるわ。![]()

![]() があるので,温度がわからなきゃダメね。Aの温度は
があるので,温度がわからなきゃダメね。Aの温度は![]() でいいとして,Cの温度はボイル・シャルルの法則で求めるの?
でいいとして,Cの温度はボイル・シャルルの法則で求めるの?![]() だから,Cの温度も
だから,Cの温度も![]() ね。
ね。![]() はどっちの温度からどっちの温度を引けばいいの?
はどっちの温度からどっちの温度を引けばいいの?
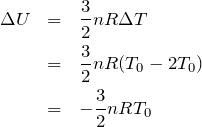
![]() がマイナスになるので,
がマイナスになるので,![]()
![]()
![]() と
と![]() を入れると,
を入れると,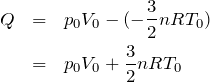
![]() が
が![]() の何倍か,ということよ。
の何倍か,ということよ。![]() が邪魔だわ。
が邪魔だわ。![]() が使えなくて,
が使えなくて,![]() で表したいんだよ。
で表したいんだよ。
![]()
![]() はどうなるかな?
はどうなるかな?