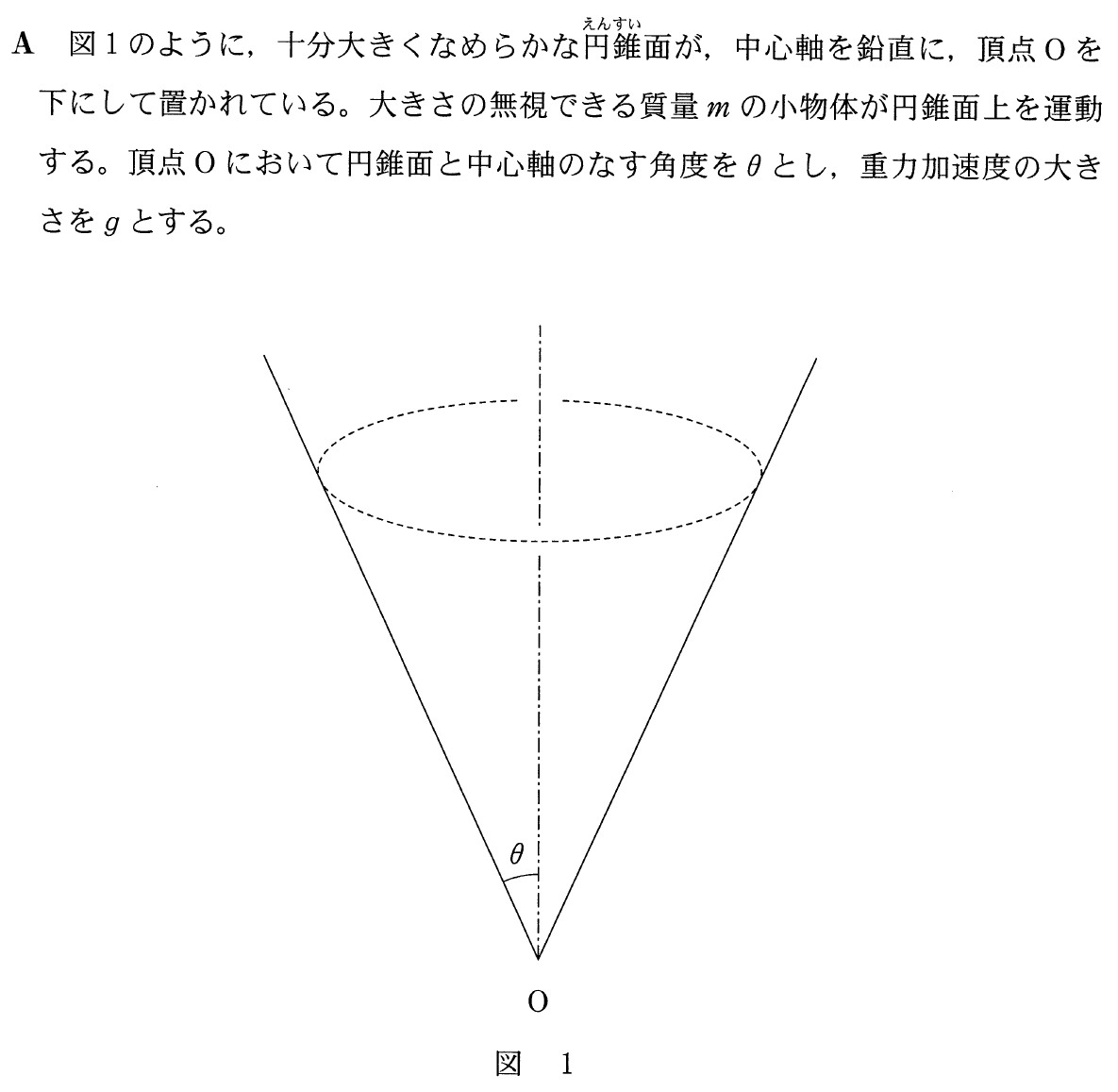
■平面的な図に描き直す
物理が苦手な文子
円錐面ってあんまり見たことがないけど,どんなイメージなの?
物理が得意な秀樹
パーティーのときにかぶる円錐形のとんがり帽子とか,ソフトクリームのコーンみたいな感じだよね。ソフトクリームの「コーン」って,そもそも「円錐」っていう意味だからね。
物理が苦手な文子
へー,そうなの。とうもろこしの「コーン」じゃないんだ。
物理が得意な秀樹
円錐はcone,とうもろこしはcornだね。まぁ,とりあえずその円錐面の内側を小物体がすべり降りるんだね。
物理が苦手な文子
単に斜面をすべり降りる問題と考えていいの?
物理が得意な秀樹
そういうことだよね。そう考えると,よくある問題でしょ。
物理が苦手な文子
でも図が立体的に描かれているので,力の矢印が描きにくいわ。
物理が得意な秀樹
問題にある図に描き込むんじゃなくて,平面的な図に描き直したほうがいいよ。
物理が苦手な文子
やっぱりそうだよね。手前から見た図を描いてみると,こんな感じかな?
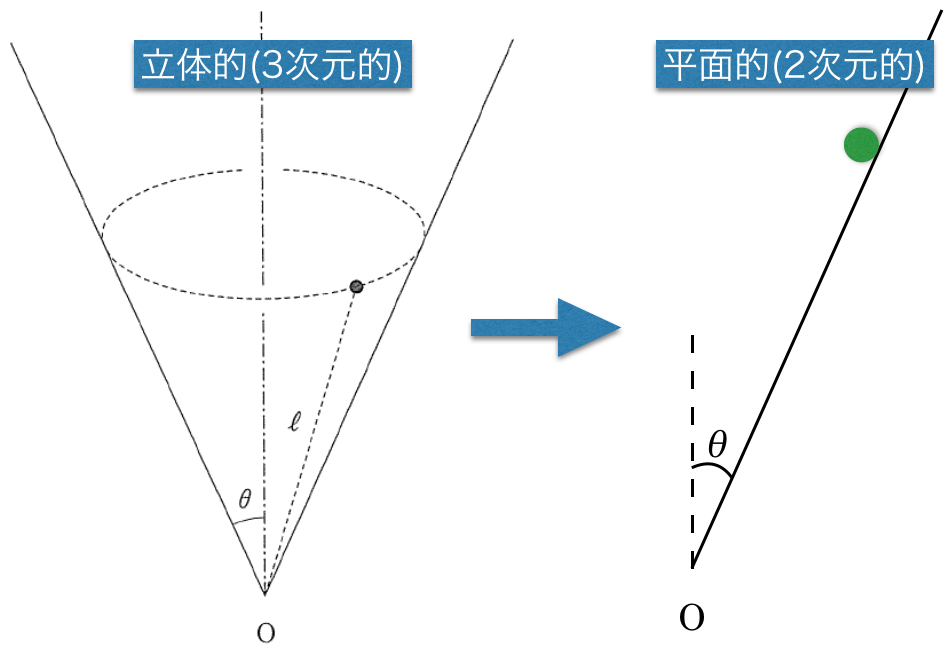
物理が得意な秀樹
それでいいね。少し簡単にできる方法もあるんだけど,先に通常のやり方で問いてみよう。
物理が苦手な文子
きっとまずは力の矢印を描くのよね。
物理が得意な秀樹
そうだね。

物理が苦手な文子
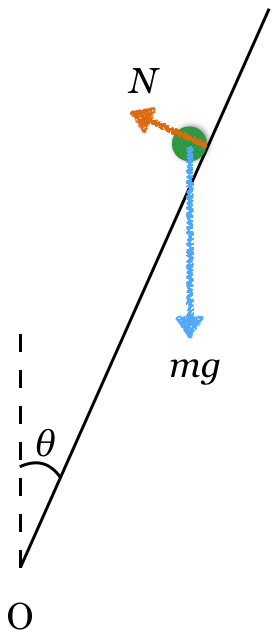
重力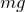 と,あとくっついているのは円錐面だけだから,円錐面から受ける垂直抗力
と,あとくっついているのは円錐面だけだから,円錐面から受ける垂直抗力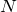 ね。
ね。
物理が得意な秀樹
その2力だけだね。次は重力を斜面方向と,斜面に垂直な方向に分けてみようか。ついでに,角度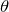 がどこか分かるかな。
がどこか分かるかな。
■θの位置がいつもと違う
物理が苦手な文子
たぶん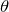 はここよね。
はここよね。
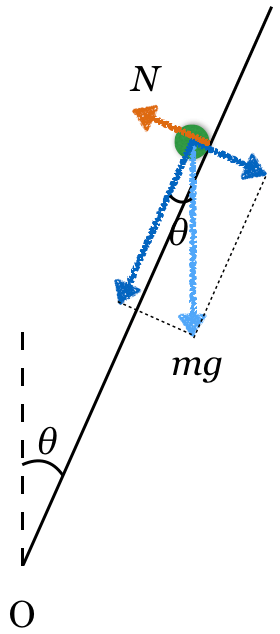
物理が得意な秀樹
そうだね。実は,一般的に斜面を滑り降りる問題では,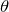 が水平面とのなす角で与えられるんだけど,この問題は鉛直面とのなす角なんだよね。
が水平面とのなす角で与えられるんだけど,この問題は鉛直面とのなす角なんだよね。
物理が苦手な文子
たしかにそうね。なんとなくいつも描いている図と違う感じがしたわ。
物理が得意な秀樹
分解した2つの力の大きさは分かるかな?
物理が苦手な文子
たしか,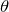 とくっついているか,向かい合っているかで分かるのよね。
とくっついているか,向かい合っているかで分かるのよね。
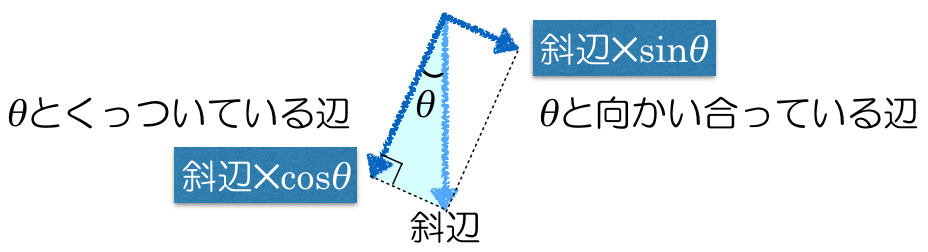
物理が得意な秀樹
そうだね,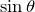 と
と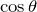 の関係がいつもと逆になるんだね。
の関係がいつもと逆になるんだね。
物理が苦手な文子
これでいいわよね。
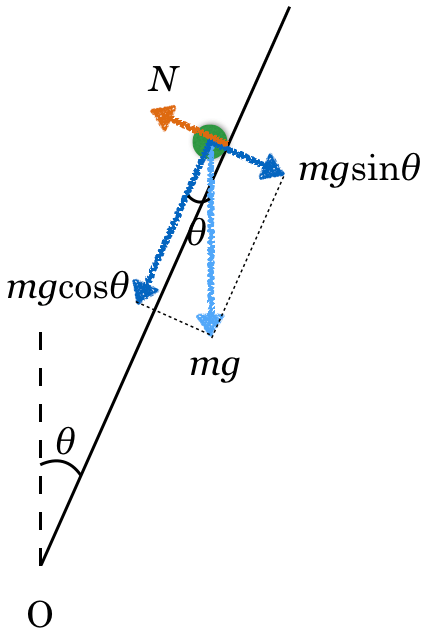
物理が得意な秀樹
最後に斜面下向きの加速度と,その向きを正にとって図を描こう。
物理が苦手な文子
これで図は完成?
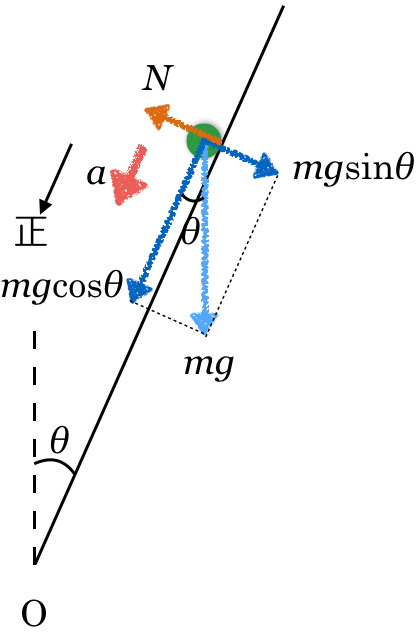
■図が完成したら,運動方程式
物理が得意な秀樹
完成だ。あとは正の向きの運動方程式を書こう。
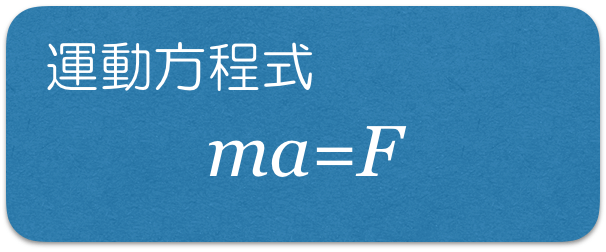
物理が苦手な文子
図に合わせて運動方程式を書くと,
![]()
![]()
■加速度が分かったら,等加速度直線運動の式
物理が得意な秀樹
これで加速度が求まったね。あとは,等加速度直線運動の公式を使って,時間を求めよう。どの式を使うかな?

物理が苦手な文子
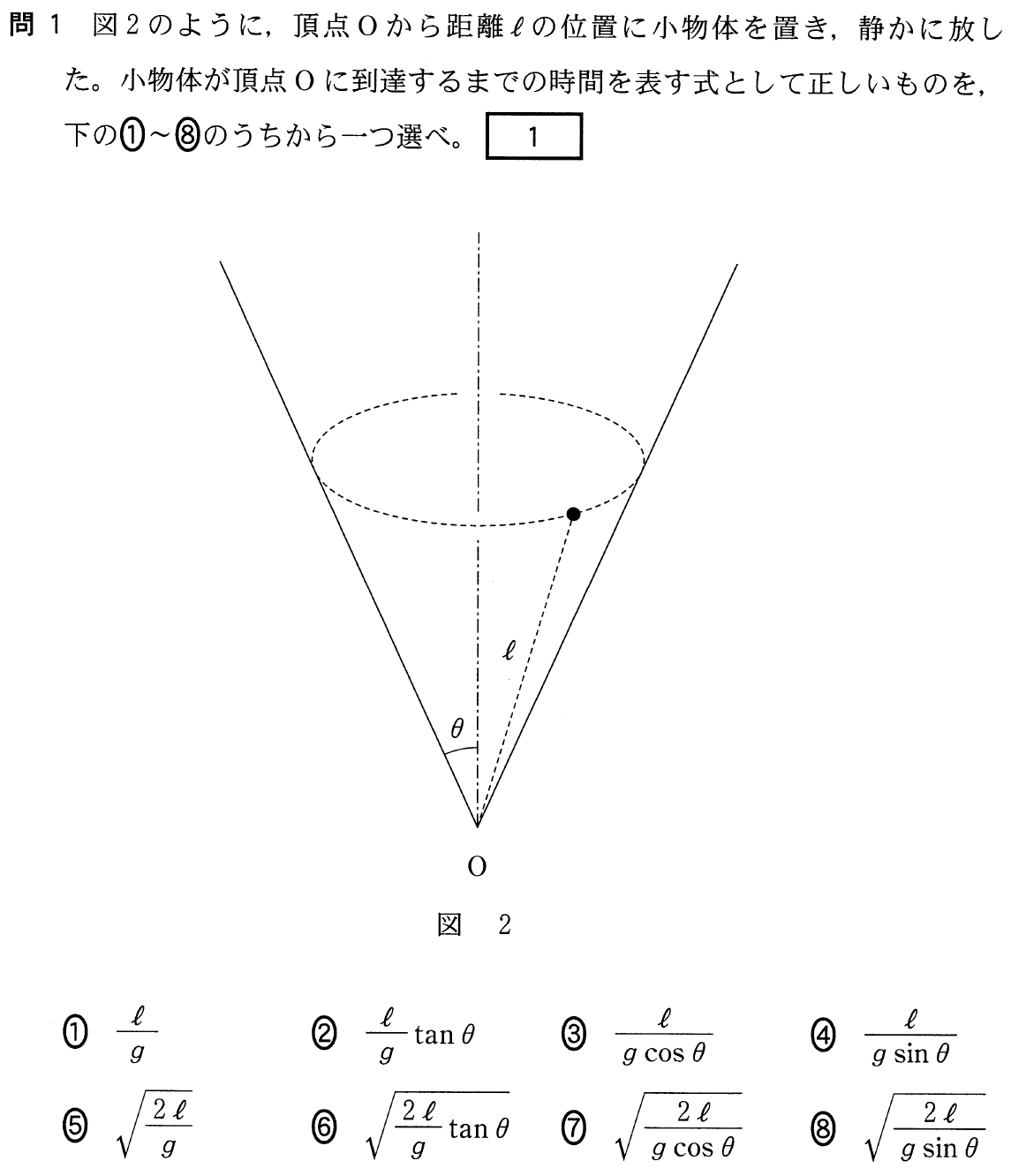
分かっているのは,問題文に「静かに放した」とあるので,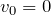 ,距離が
,距離が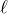 ,加速度が
,加速度が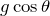 ,求めたいのが時間
,求めたいのが時間 だから,2番めの式ね。
だから,2番めの式ね。
![]() より,
より,
![]()
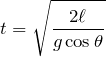
物理が得意な秀樹
正解だ。答えは⑦だね。
■摩擦がなければ,重力加速度を分解しても良い
物理が苦手な文子
そういえばさっき,簡単な方法があるとかって言ってたわよね。
物理が得意な秀樹
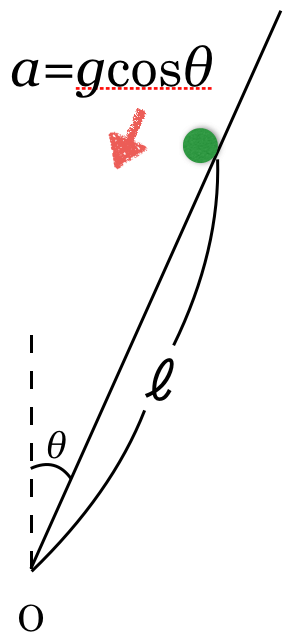
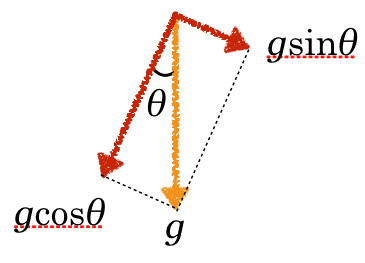
そうだったね。この問題のように,摩擦がない斜面を降りる問題では,斜面方向の加速度は,重力加速度を斜面方向に分解しても良かったんだ。
物理が苦手な文子
えっ,それだけでいいの?今はこの斜面方向の加速度を求めるために,力の矢印を描いて,力を分解して,運動方程式を立てて,加速度を求めたのよ。
物理が得意な秀樹
最初のやり方だと,どんな場合でも対応できるんだ。この重力加速度を分けるやり方は,斜面方向に他の力がはたらいていないときしか使えないんだよ。
物理が苦手な文子
どっちも知っていると便利ね。
物理が得意な秀樹
次の問2にいこう。
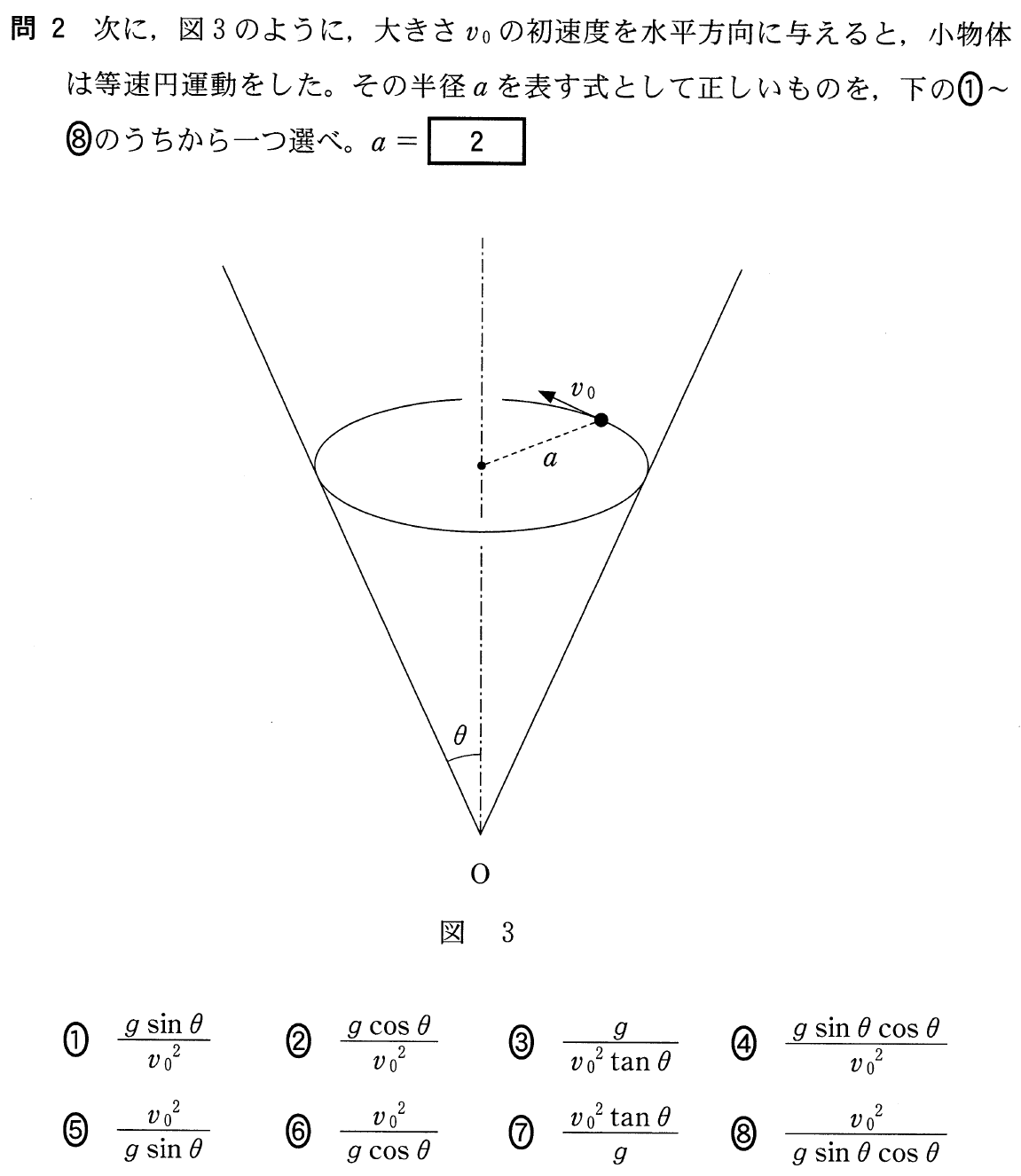
■やっぱり平面的な図に描き直す
物理が苦手な文子
今度は等速円運動ね。
物理が得意な秀樹
これも図を平面的に描こうか。ただ,さっきと同じように手前から見た図と,上から見た図の2つがあるといいかな。
物理が苦手な文子
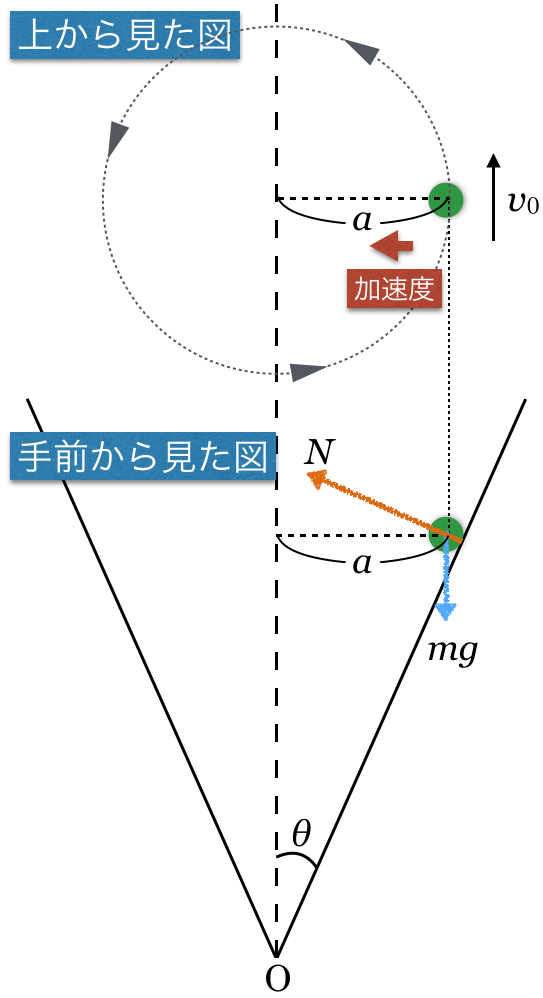
なかなか大変ですけど,こんな感じですか?
物理が得意な秀樹
いいね。
物理が苦手な文子
手前から見た図で,力の矢印は重力と,垂直抗力の2つですよね。さっきと同じ。
物理が得意な秀樹
垂直抗力の大きさは変わるけど,重力と垂直抗力の2力っていうのは変わらないね。
■力は加速度の向きに分ける
物理が苦手な文子
次はどうするの?
物理が得意な秀樹
上から見た図に描いてあるけど,等速円運動をしているので,加速度の向きは円の中心方向だよね。なので,円の中心方向にはたらいている力を求めたいんだ。
物理が苦手な文子
そうか,さっきは斜面下方向に加速していたから,斜面下方向の力を求めたのね。今は円の中心方向に加速度を持っているから,円の中心方向の力を求めるのね。
物理が得意な秀樹
ということは,この場合は垂直抗力を分けるんだね。
物理が苦手な文子
こんな感じ?
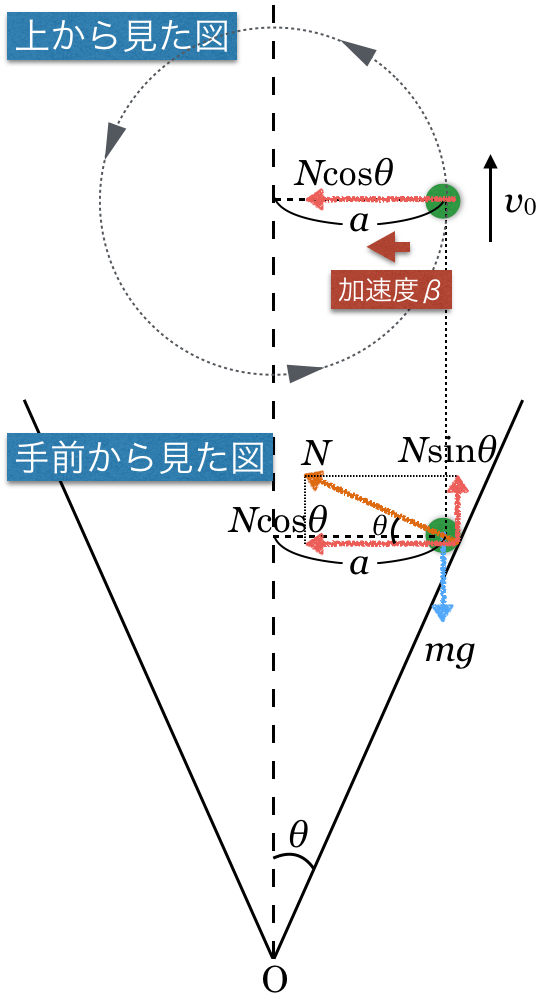
物理が得意な秀樹
円の中心方向の加速度の大きさは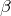 にしておこう。本当は
にしておこう。本当は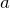 にしたいけど,
にしたいけど,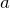 は円運動の半径として,使われているからね。
は円運動の半径として,使われているからね。
物理が苦手な文子
加速度があるということは,運動方程式を立てるのね。
物理が得意な秀樹
そうだね。円の中心方向を正として,運動方程式を立ててみようか。
物理が苦手な文子
![]()
■等速円運動で使われる式の確認
物理が得意な秀樹
等速円運動の加速度の式は覚えてるかな?
物理が苦手な文子
なんとなく,こんな感じかな?

物理が得意な秀樹
そうだね。このうち,どれか一つ覚えれば,等速円運動の速さの式で変形できるんだよね。

物理が苦手な文子
これを使って,変形すると,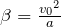 より,
より,
![]()
物理が苦手な文子
こうなるけど,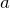 を求めたいけど
を求めたいけど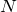 が消えないわね。
が消えないわね。
物理が得意な秀樹
今度は手前から見た図で,鉛直方向の力のつりあいの式を立てるんだ。
物理が苦手な文子
なるほど。鉛直上向きを正として,力のつりあいの式を立てるわね。
![]()
![]()
物理が得意な秀樹
そうだね。ということは,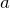 が求まるかな?
が求まるかな?
物理が苦手な文子
えっと,
![]()
![]()
物理が得意な秀樹
いいね。答えは⑦だ。最後に問3。
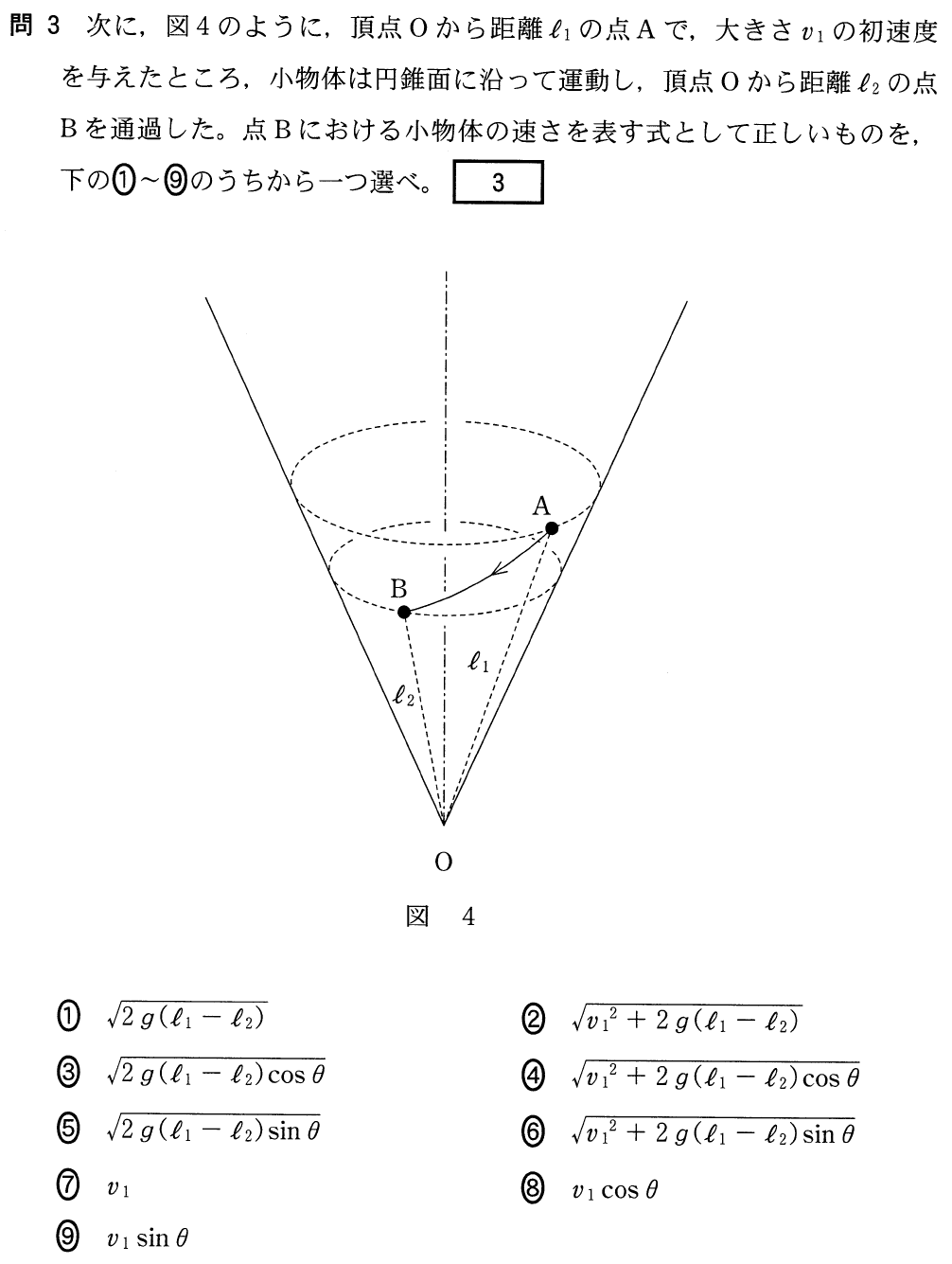
■向きがわからない
物理が苦手な文子
また立体的な図だけど,今度は平面的な図に描きにくいわ。
物理が得意な秀樹
たしかにそうだね。でもポイントさえわかれば描けるよ。
物理が苦手な文子
ポイントどころか,いろいろと分からないわ。初速度の大きさ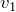 を与えたみたいだけど,速度の向きもわからないし,点Bでの速度の向きも全くわからないし。
を与えたみたいだけど,速度の向きもわからないし,点Bでの速度の向きも全くわからないし。
物理が得意な秀樹
向きがわからないということは,向きが関係ない式を使うということだ。
物理が苦手な文子
えっ?どういうこと?
物理が得意な秀樹
今までのように力の矢印を描くときは,向きが大切だよね。ということは,今は力は関係ないね。
物理が苦手な文子
力が関係ないということは,あとは何ができるかな?
物理が得意な秀樹
高さが変わることで,速さが変わるんだから…
物理が苦手な文子
高さと速さの関係といえば,「力学的エネルギー保存の法則」かな?
物理が得意な秀樹
そうだよ。なので,高さと速さがわかればいいので,高さと速さが分かる図が描けるかな。
物理が苦手な文子
そこがポイントね。こんな感じ?
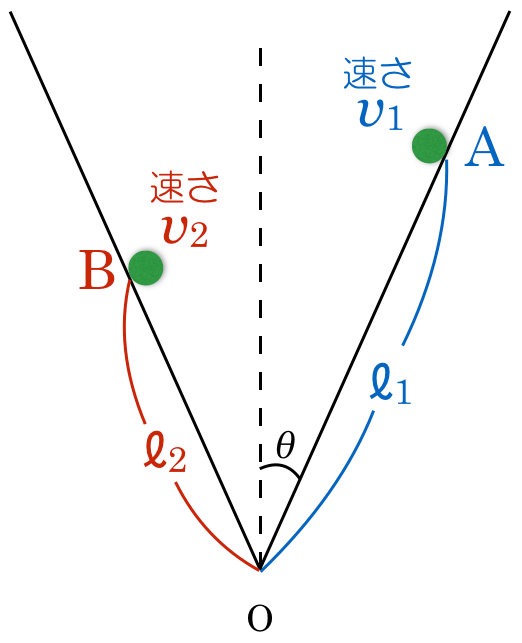
物理が得意な秀樹
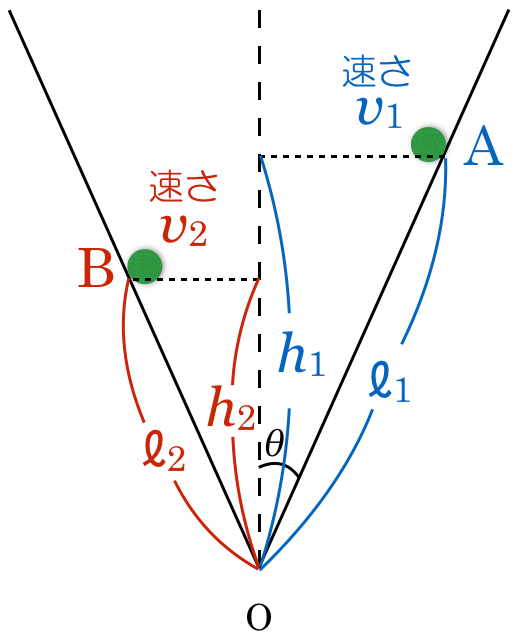
物理が苦手な文子
これは簡単。
![]()
![]()
物理が得意な秀樹
いいね。それでは,力学的ネルギー保存の法則を使って式を立ててみようか。
物理が苦手な文子
Oの高さを基準として,AとBで力学的エネルギー保存の法則を立てるわ。
Aの力学的エネルギー=Bの力学的エネルギー
![]()
![]()
![]()
![]()
物理が得意な秀樹
正解だ。答えは④だね。