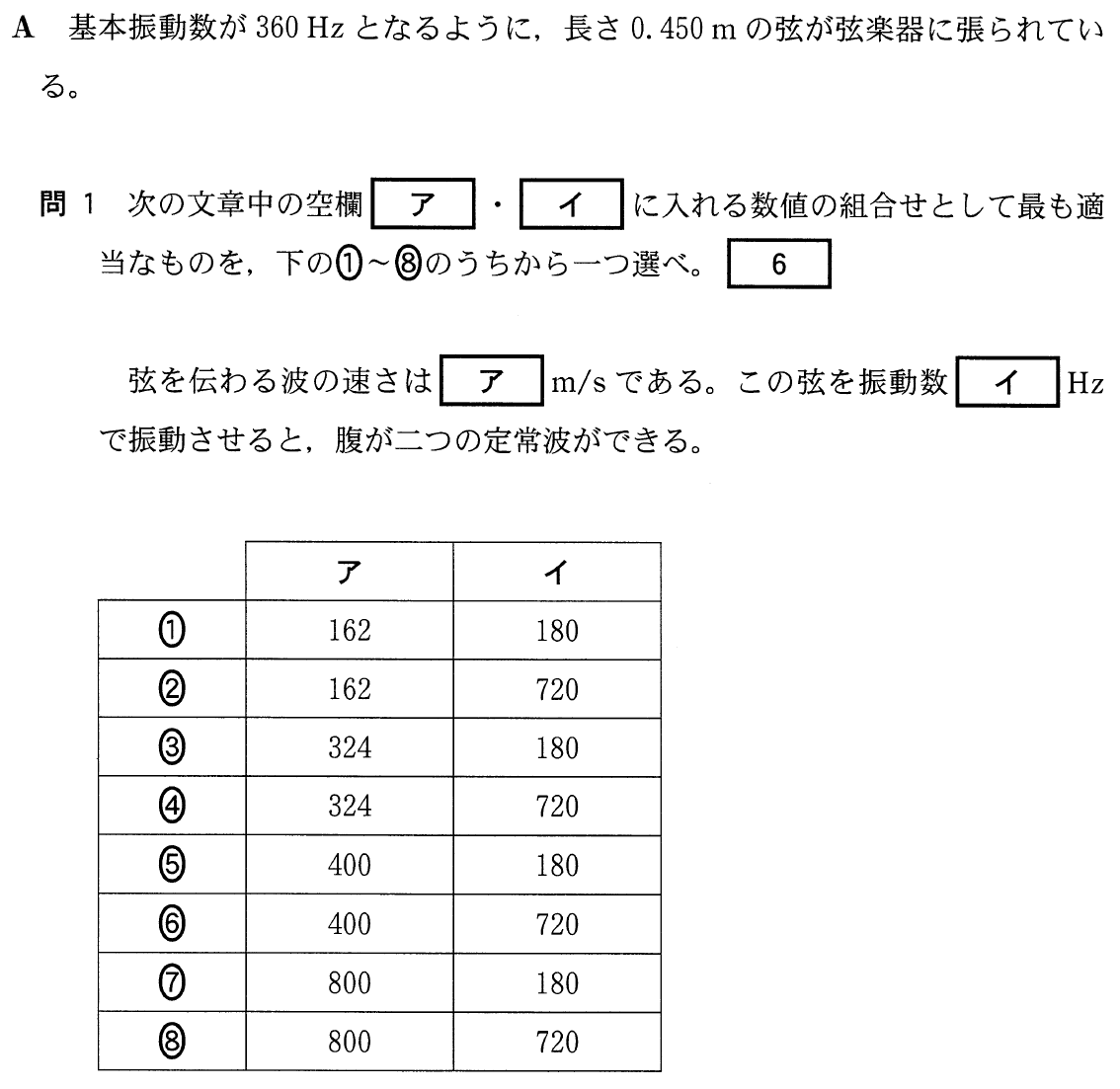
■問題文から波長を求める

![]() を求めたくて,振動数
を求めたくて,振動数![]() が分かっているから,波長
が分かっているから,波長![]() が分かればいいんだよね。
が分かればいいんだよね。
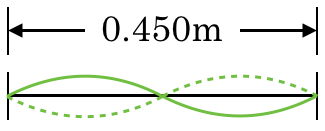
■図を描くことはとにかく大切
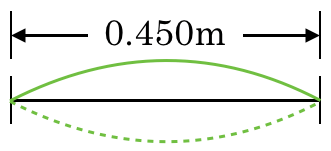
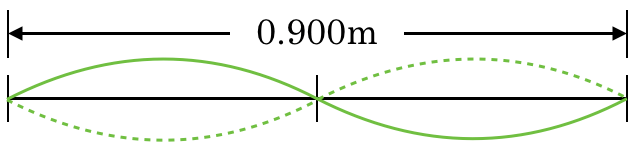
![]() =0.900mだね。
=0.900mだね。
![]() は,
は,
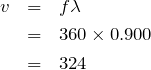
![]() より,
より,


■物理の絶対値は難しくない
![]() が,振動数の差だね。
が,振動数の差だね。

![]() Hz,おんさの振動数を
Hz,おんさの振動数を![]() とするよ。4秒間に8回のうなりが聞こえたということは?
とするよ。4秒間に8回のうなりが聞こえたということは?
![]()
![]() は次の2つしか考えられないんだ。
は次の2つしか考えられないんだ。
![]() が360より大きければ,
が360より大きければ,![]() =362Hz
=362Hz
![]() が360より小さければ,
が360より小さければ,![]() =358Hz
=358Hz
![]() Hzね。
Hzね。
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() を求めたくて,振動数
を求めたくて,振動数![]() が分かっているから,波長
が分かっているから,波長![]() が分かればいいんだよね。
が分かればいいんだよね。


![]() =0.900mだね。
=0.900mだね。
![]() は,
は,
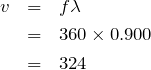

![]() より,
より,


![]() が,振動数の差だね。
が,振動数の差だね。

![]() Hz,おんさの振動数を
Hz,おんさの振動数を![]() とするよ。4秒間に8回のうなりが聞こえたということは?
とするよ。4秒間に8回のうなりが聞こえたということは?
![]()
![]() は次の2つしか考えられないんだ。
は次の2つしか考えられないんだ。
![]() が360より大きければ,
が360より大きければ,![]() =362Hz
=362Hz
![]() が360より小さければ,
が360より小さければ,![]() =358Hz
=358Hz
![]() Hzね。
Hzね。