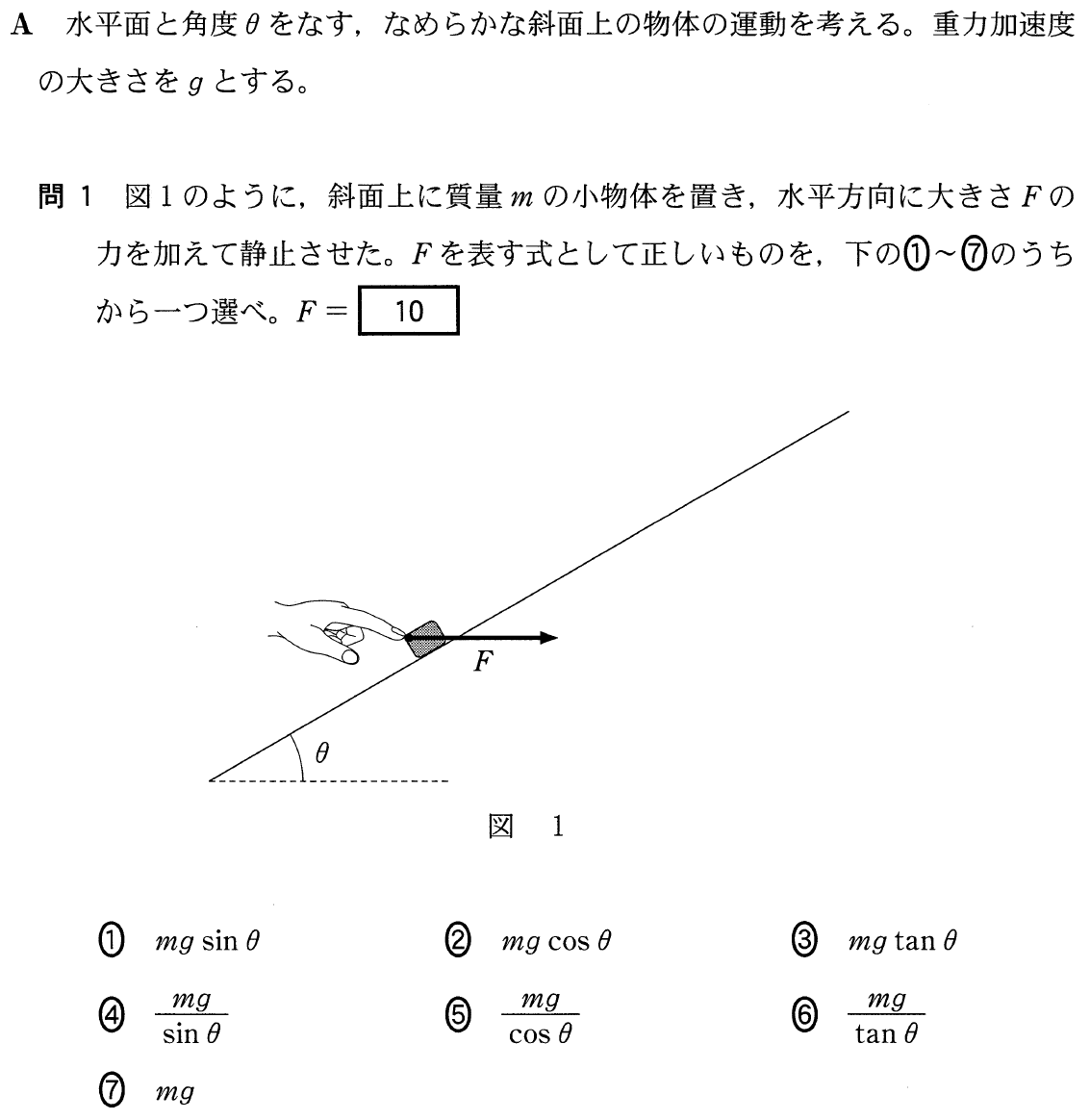
■とにかく力の矢印を描く

![]() と描かれているので,斜面から受ける垂直抗力を
と描かれているので,斜面から受ける垂直抗力を![]() とすれば,力の矢印は終わりね。
とすれば,力の矢印は終わりね。
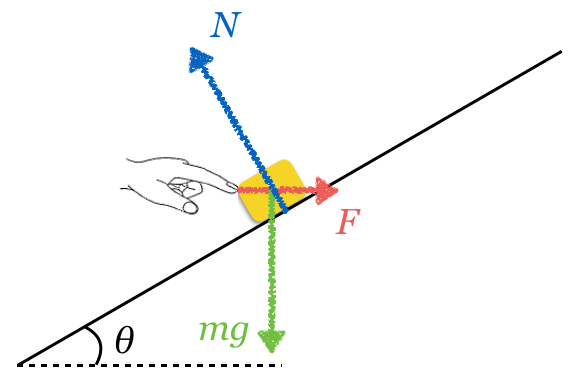
■力のつりあいの式を立てる
![]() を分解するのがいいかな?
を分解するのがいいかな?
![]() の正の向き,鉛直上向きを
の正の向き,鉛直上向きを![]() の正の向きとして,
の正の向きとして,![]() を分解して,力のつりあいの式を立ててみようか。
を分解して,力のつりあいの式を立ててみようか。
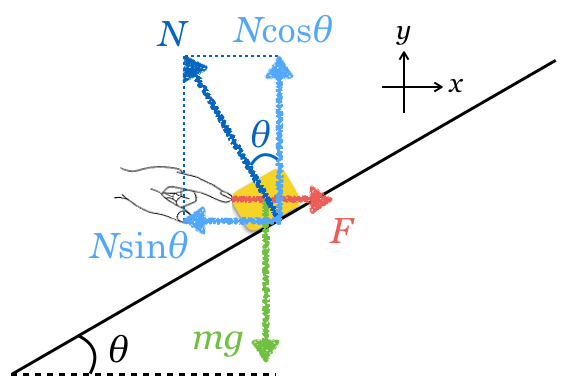
![]() 方向:
方向:![]()
![]() 方向:
方向:![]()
![]() だよね。
だよね。
![]() を消去するわね。
を消去するわね。
![]() より,
より,
![]()
![]() に代入
に代入
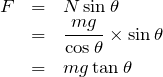
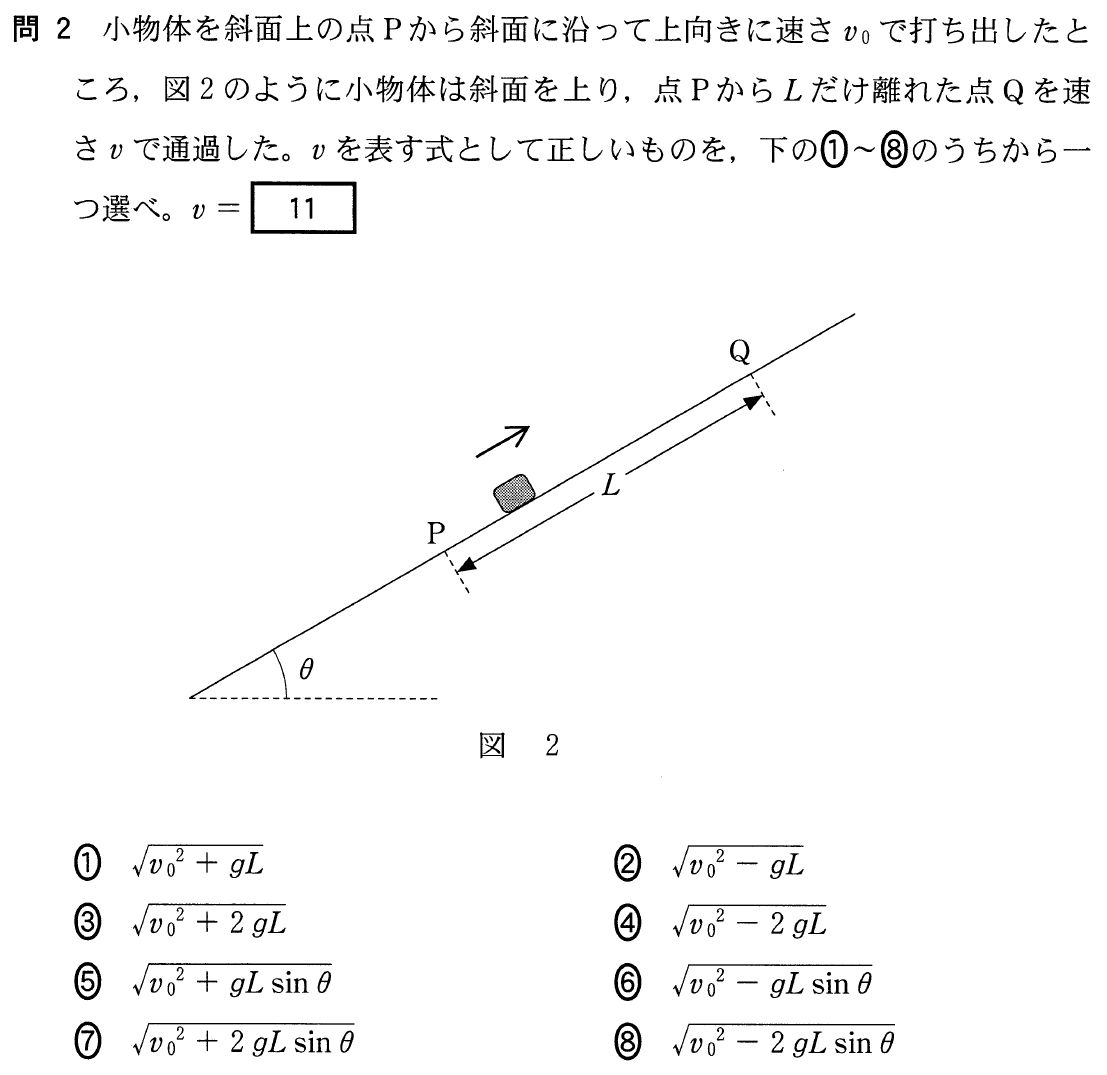
■力学的エネルギー保存則を使うことにする
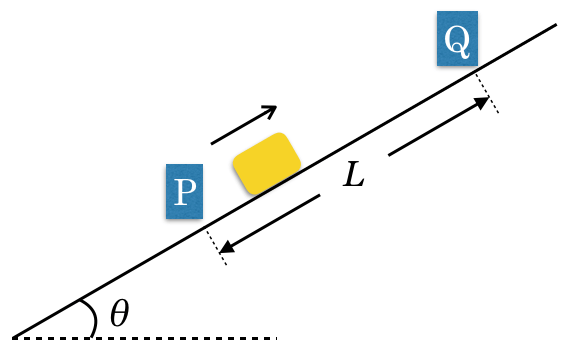

![]() とすると,こんな感じ?
とすると,こんな感じ?
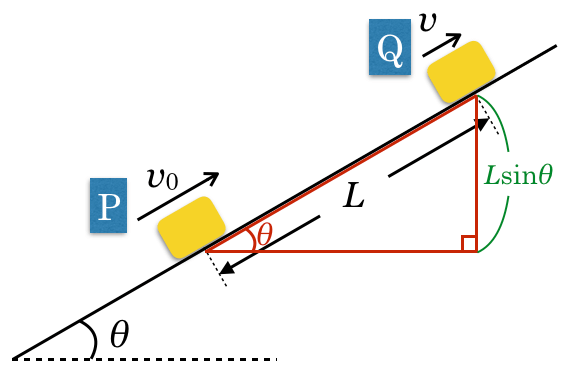
■確実に確認して式を立てる
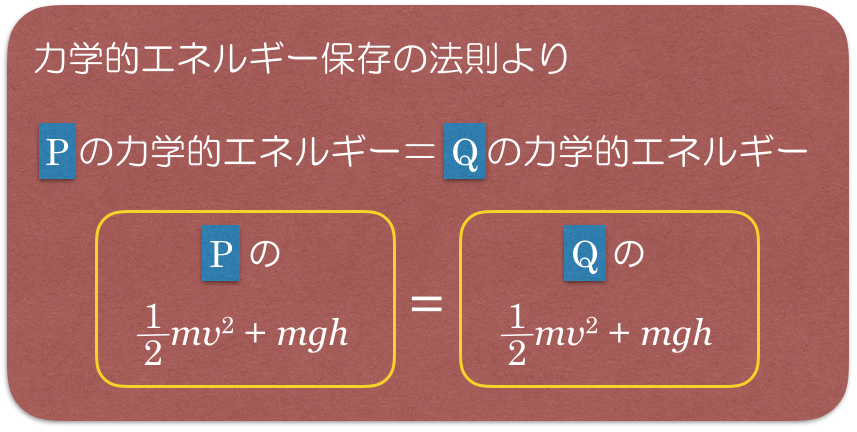
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!


![]() と描かれているので,斜面から受ける垂直抗力を
と描かれているので,斜面から受ける垂直抗力を![]() とすれば,力の矢印は終わりね。
とすれば,力の矢印は終わりね。

![]() を分解するのがいいかな?
を分解するのがいいかな?
![]() の正の向き,鉛直上向きを
の正の向き,鉛直上向きを![]() の正の向きとして,
の正の向きとして,![]() を分解して,力のつりあいの式を立ててみようか。
を分解して,力のつりあいの式を立ててみようか。

![]() 方向:
方向:![]()
![]() 方向:
方向:![]()
![]() だよね。
だよね。
![]() を消去するわね。
を消去するわね。
![]() より,
より,
![]()
![]() に代入
に代入
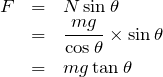



![]() とすると,こんな感じ?
とすると,こんな感じ?


![]()
![]()