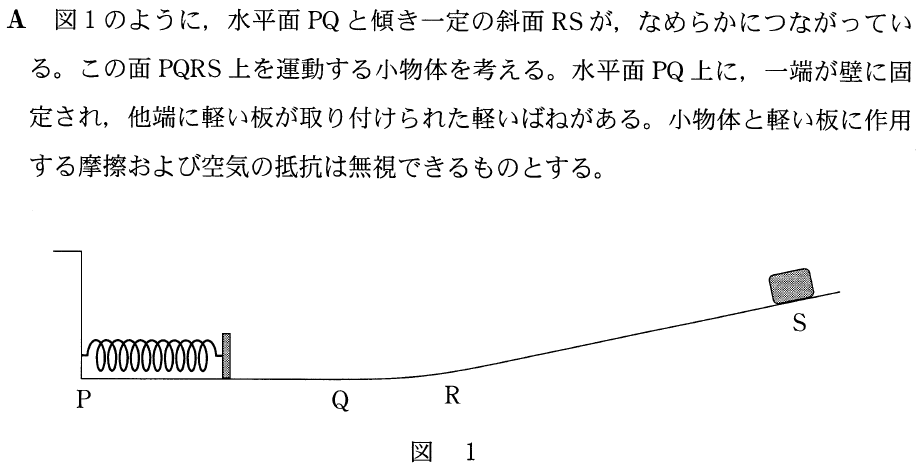

■v-tグラフから加速度と移動距離を読み取る
物理が苦手な文子
物理が得意な秀樹
そうだね。縦軸が速さを表す で,横軸が時間を表す
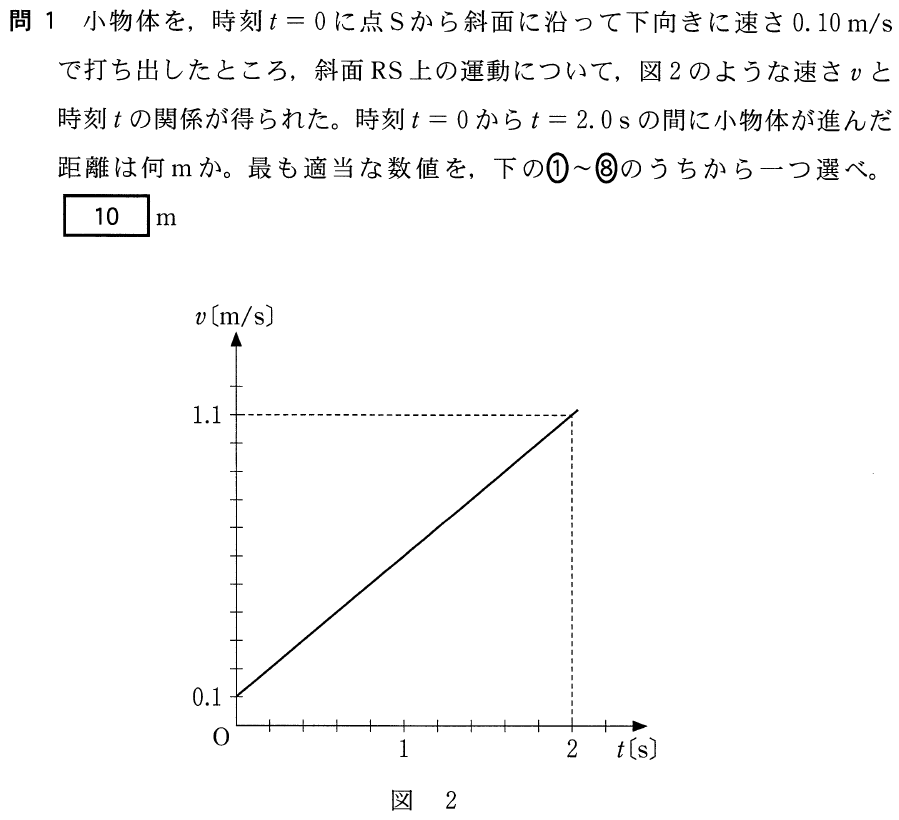
で,横軸が時間を表す のグラフから,進んだ距離を求めようということだね。図1にある斜面の角度が分かれば,進んだ距離を求められるんだけど,この問題では角度が分からないから,グラフから進んだ距離を求めなきゃダメだね。
のグラフから,進んだ距離を求めようということだね。図1にある斜面の角度が分かれば,進んだ距離を求められるんだけど,この問題では角度が分からないから,グラフから進んだ距離を求めなきゃダメだね。
物理が苦手な文子
グラフから進んだ距離が簡単に求められるような記憶があるけど,どうすれば良いのかは覚えていないわ。
物理が得意な秀樹
ポイントは,「グラフの傾き」と「横軸と囲む面積」だね。

物理が苦手な文子
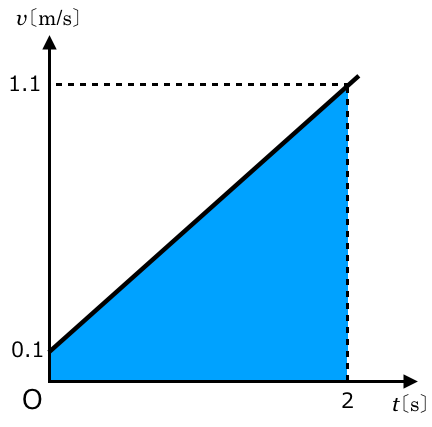
そう言われれば,そうだった気がする。今は「進んだ距離」を求めたいから,グラフの面積を求めればいいのね。ここの部分よね。
物理が得意な秀樹
そうだね。その台形の面積を求めればいいね。
物理が苦手な文子
そういうことね。求める距離を とすると,
とすると,
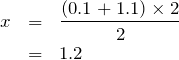
物理が得意な秀樹
いいね。答えは④だ。次は問2。

■ばねが最も縮んだときの速さは0
物理が苦手な文子
ばねの縮みを求める問題ね。フックの法則を使うの?
物理が得意な秀樹
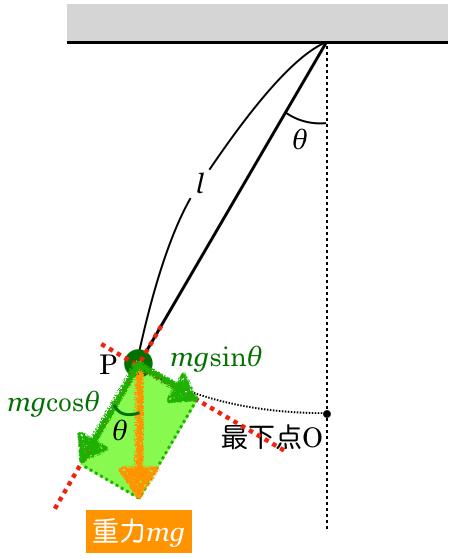
ばねがあるときは,フックの法則を使うことが多いよね。フックの法則は,ばねの力とばねの伸びの関係を表しているけど,この問題では「力」はあまり使えないんだ。ばねが最も縮んだときの「力」が分かればいいんだけど,分からないんだな。
物理が苦手な文子
フックの法則が使えないとすると,どうすればいいの?
物理が得意な秀樹
小物体が板にぶつかるときの速さが分かっているから,「力学的エネルギー保存の法則」が使えそうだね。
物理が苦手な文子
「力学的エネルギー保存の法則」って,良く聞くけど,どうやって使えばいいの?
物理が得意な秀樹
問題文に与えられている情報を整理していくと,だんだん分かってくると思うよ。「力学的エネルギー保存の法則」は,ある瞬間とある瞬間で力学的エネルギーが保存するっていう法則だから,2つの瞬間の情報を整理するんだ。
物理が苦手な文子
それじゃあ,小物体が板にぶつかる前を考えるわ。
物理が得意な秀樹
そのときを「A」として,図の中に情報を書いていこう。
物理が苦手な文子
こんな感じでいいの?
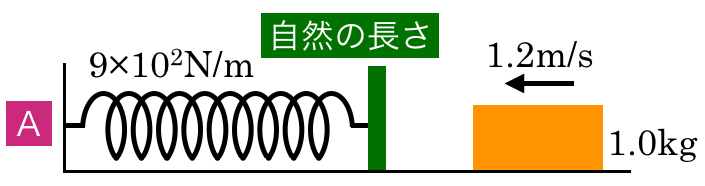
物理が得意な秀樹
これだけの情報があれば,完璧だね。それじゃあ,もう1つはばねが最も縮んだ瞬間を考えようか。その瞬間を「B」として,ばねの縮みを としよう。
としよう。
物理が苦手な文子
こういうこと?
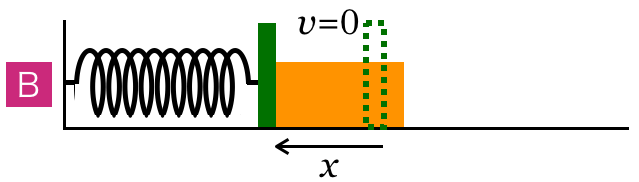
物理が得意な秀樹
そうだね。ばねが最も縮んだとき,小物体の速さは0になるんだよね。情報の整理はこれで完璧だ。
物理が苦手な文子
次はどうすればいいの?
物理が得意な秀樹
この「A」と「B」の2つの瞬間で,力学的エネルギー保存の法則の式を立てるんだ。

物理が苦手な文子
なるほど。力学的エネルギーって,「運動エネルギーと位置エネルギーの和」よね。
物理が得意な秀樹
そうだね。位置エネルギーって,重力による位置エネルギーと弾性力による位置エネルギーがあるけど,今は鉛直方向には運動していないから,重力による位置エネルギーは考えなくていいね。

物理が苦手な文子
ということは,「A」の運動エネルギー+弾性力による位置エネルギー=「B」の運動エネルギー+弾性力による位置エネルギーっていう式を立てればいいのね。
物理が得意な秀樹
速さが0であれば運動エネルギーは0だし,ばねが自然の長さであれば弾性力による位置エネルギーは0だからね。
物理が苦手な文子
計算してみるわ。
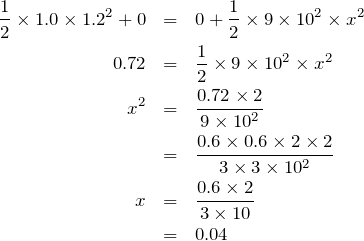
物理が得意な秀樹
結構計算がたいへんだったね。正解は③だ。