センター2017物理基礎追試第３問Ｂ「力の分解，力学的エネルギー保存則」

2017.06.17

スポンサーリンク

■重力が対角線になるような長方形を描く

物理が苦手な文子
重力の成分を考える問題ね。
物理が得意な秀樹
図さえ描ければ答えは出ると思うんだけどどうかな？
物理が苦手な文子
図の描き方を教えてよ。
物理が得意な秀樹
じゃあ，順番に描いていこうか。まずは小球にはたらく重力の矢印を描こう。
物理が苦手な文子
重力は下向きに描けばいいのよね。

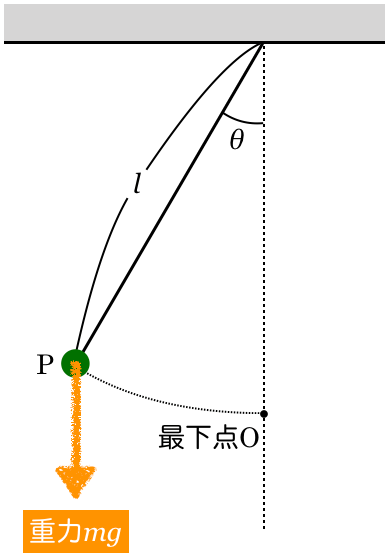
物理が得意な秀樹
そうだね。質量が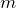mだから，重力の大きさは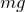mgになるね。
物理が苦手な文子
次はどうすればいいの？
物理が得意な秀樹
この重力を糸に平行な成分と，糸に垂直な成分に分けるんだよね。その向きを確認しておこうか。重力の矢印の根元を通って，糸に平行な方向はどうなるかな？
物理が苦手な文子
矢印の根元を通るなら，糸に平行というよりは，糸の延長線と同じね。

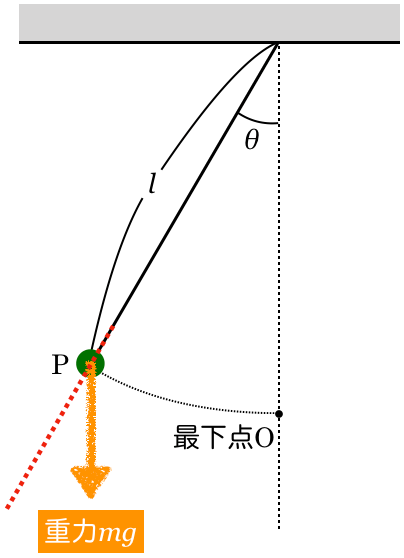
物理が得意な秀樹
次は同じように，重力の矢印の根元を通って，糸に垂直な方向も描いちゃおうか。

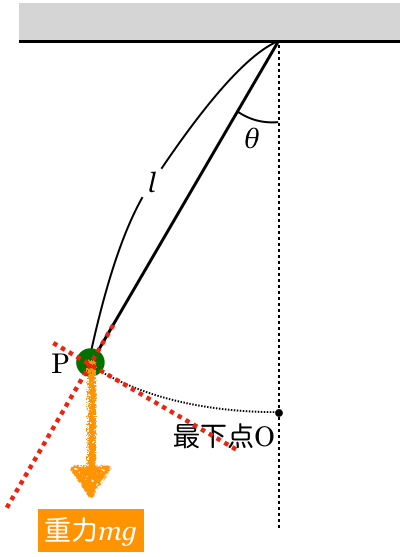
物理が苦手な文子
この２つの方向に重力を分ければいいのね。で，どうするの？
物理が得意な秀樹
大切なポイントは，重力の矢印が対角線になるような長方形を描くんだ。長方形の辺は，今描いた糸に平行な方向と垂直な方向ね。
物理が苦手な文子
こんな感じでいい？

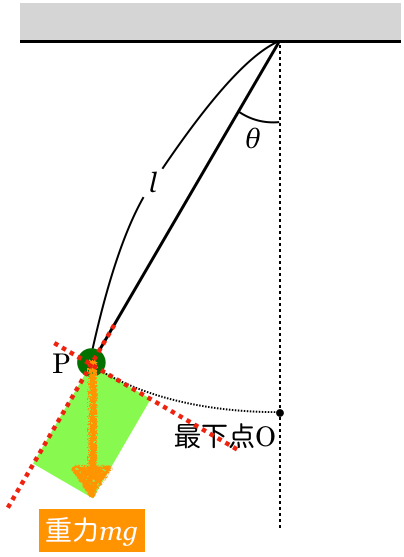
物理が得意な秀樹
いいね。で，その長方形の辺の長さが重力を分けた成分になるんだ。

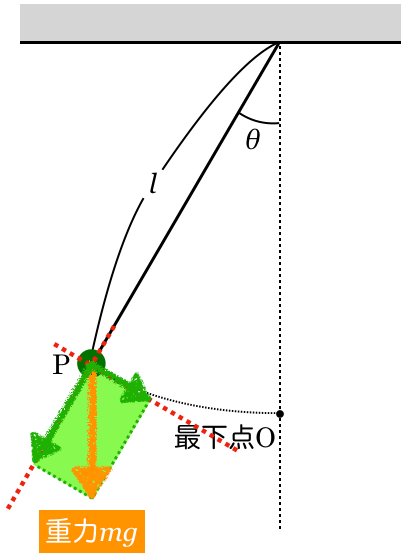
物理が苦手な文子
この矢印の長さを求めればいいということね。
物理が得意な秀樹
そういうことだ。どうすればいいか分かる？
物理が苦手な文子
どこかの角度が分かればいいわよね。
物理が得意な秀樹
そうだね。分かっている角度は天井のところの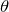\thetaだけだから，どこかにその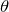\thetaがないかな。
物理が苦手な文子
ここ？

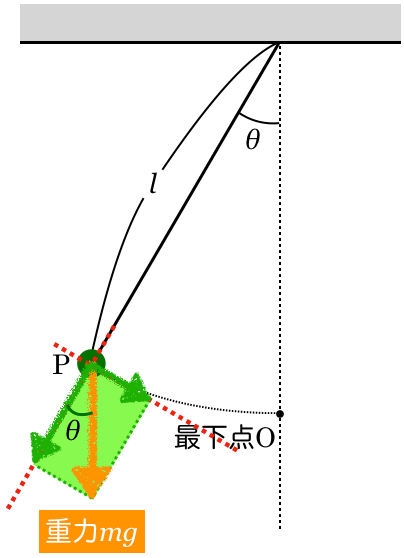
物理が得意な秀樹
そうだね。重力は鉛直方向だから，錯角の関係でそこが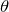\thetaだね。
物理が苦手な文子
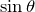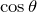あとは，\sin\thetaか，\cos\thetaなのよね。
物理が得意な秀樹
\thetaとくっついている辺の長さが，「対角線×\cos\theta」で，\thetaと向かい合っている辺の長さが「対角線×\sin\theta」だよ。
物理が苦手な文子
こういうこと？

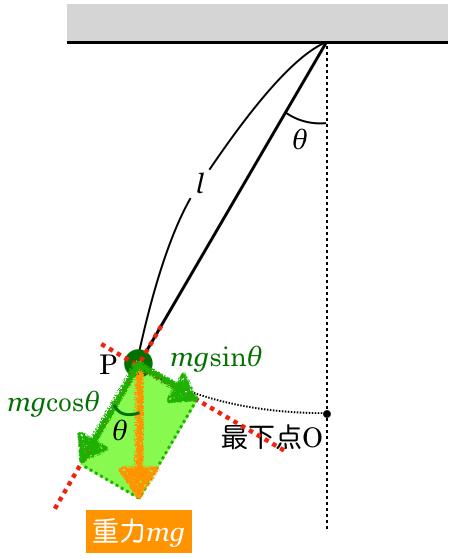
物理が得意な秀樹
そういうことだね。糸に平行な成分は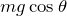mg\cos\thetaで，糸に垂直な成分は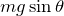mg\sin\thetaだ。なので答えは⑧だ。次は問４。

■図から高さを求める

物理が苦手な文子
最下点での小球の速さを求める問題だけど，等加速度直線運動の式を使う？
物理が得意な秀樹
残念ながらこの小球の運動は等加速度じゃないんだ。というか，直線運動でもないことは，見たらわかるでしょ。
物理が苦手な文子
そうか。直線運動じゃないから，等加速度であろうと，等速であろうと公式は使えないわね。
物理が得意な秀樹
こういうときは，「力学的エネルギー保存の法則」を考えるんだ。
物理が苦手な文子
なるほど。重力による位置エネルギーが減った分だけ運動エネルギーになるっていうことね。
物理が得意な秀樹
そういうことだね。きちんと考えると，点Pと最下点Oで力学的エネルギーが等しいという式を立てようか。

物理が苦手な文子
力学的エネルギーっていうのは，運動エネルギーと位置エネルギーの和よね。
物理が得意な秀樹
そうだね。今はばねが無いから，考えるのは運動エネルギーと重力による位置エネルギーだよ。
物理が苦手な文子
運動エネルギーは，点Pでは０と考えていいのよね。
物理が得意な秀樹
問題文に「小球を静かに放す･･･」とあるので，点Pで小球を放した時の速さは0と考えていいね。最下点での小球の速さは問題文にある通りvとしよう。
物理が苦手な文子
次は重力による位置エネルギーね。
物理が得意な秀樹
重力による位置エネルギーを考えるときには，まず基準の高さを決めるんだ。
物理が苦手な文子
そうね。最下点の高さを基準としていい？
物理が得意な秀樹
そうだね。一般的には最下点を高さの基準とするね。それじゃあ，最下点を基準とすると，点Pの高さはどう表せるかな？
物理が苦手な文子
えっと，なかなか難しいわね。分からないわ。
物理が得意な秀樹
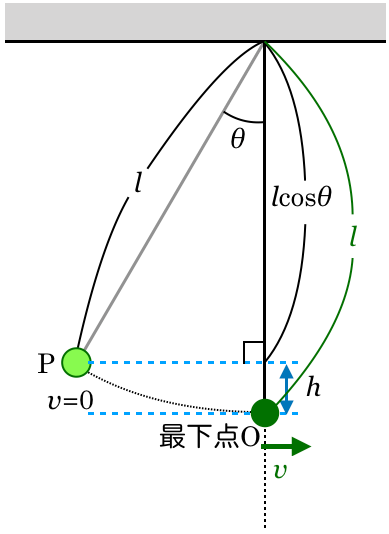
求めたい高さを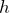hとすると，この高さだよね。

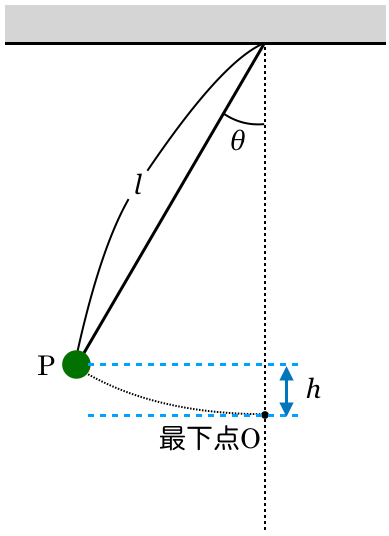
物理が苦手な文子
この高さって求めることができるの？
物理が得意な秀樹
できるよ。この図のこの直角三角形に着目しようか。

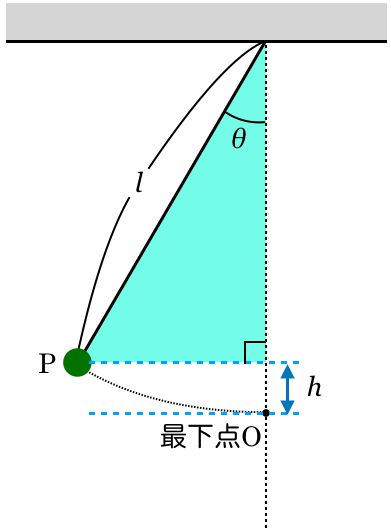
物理が得意な秀樹
そうすると，この鉛直方向の長さが分かるよね。

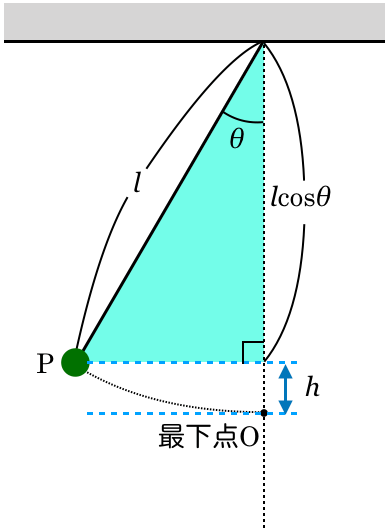
物理が苦手な文子
なんか，求まりそうな図になったけど，まだ分からないわ。
物理が得意な秀樹
小球が最下点を通ることを考えると，最下点Oから天井までの高さはちょうど糸の長さ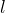lになるんだ。

物理が苦手な文子
なるほど。ということは，点Pの高さ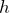hは，

    \begin{eqnarray*}h&=&l-l\cos\theta\\ &=&l(1-\cos\theta)\end{eqnarray*}

物理が得意な秀樹
それが高さになるね。それじゃあ，力学的エネルギー保存の法則に従って式を立ててみようか。一応式を確認しておくよ。

物理が苦手な文子
「点Pの力学的エネルギー＝最下点Oの力学的エネルギー」ね。

    \begin{eqnarray*}0+mg\times l(1-\cos\theta)&=& \frac{1}{2}mv^2+0\\ v^2&=&2gl(1-\cos\theta)\\ v&=&\sqrt{2gl(1-\cos\theta)}\end{eqnarray*}

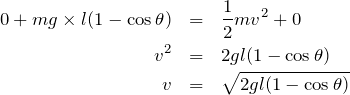
物理が得意な秀樹
正解だ。答えは⑤。
タイトルとURLをコピーしました