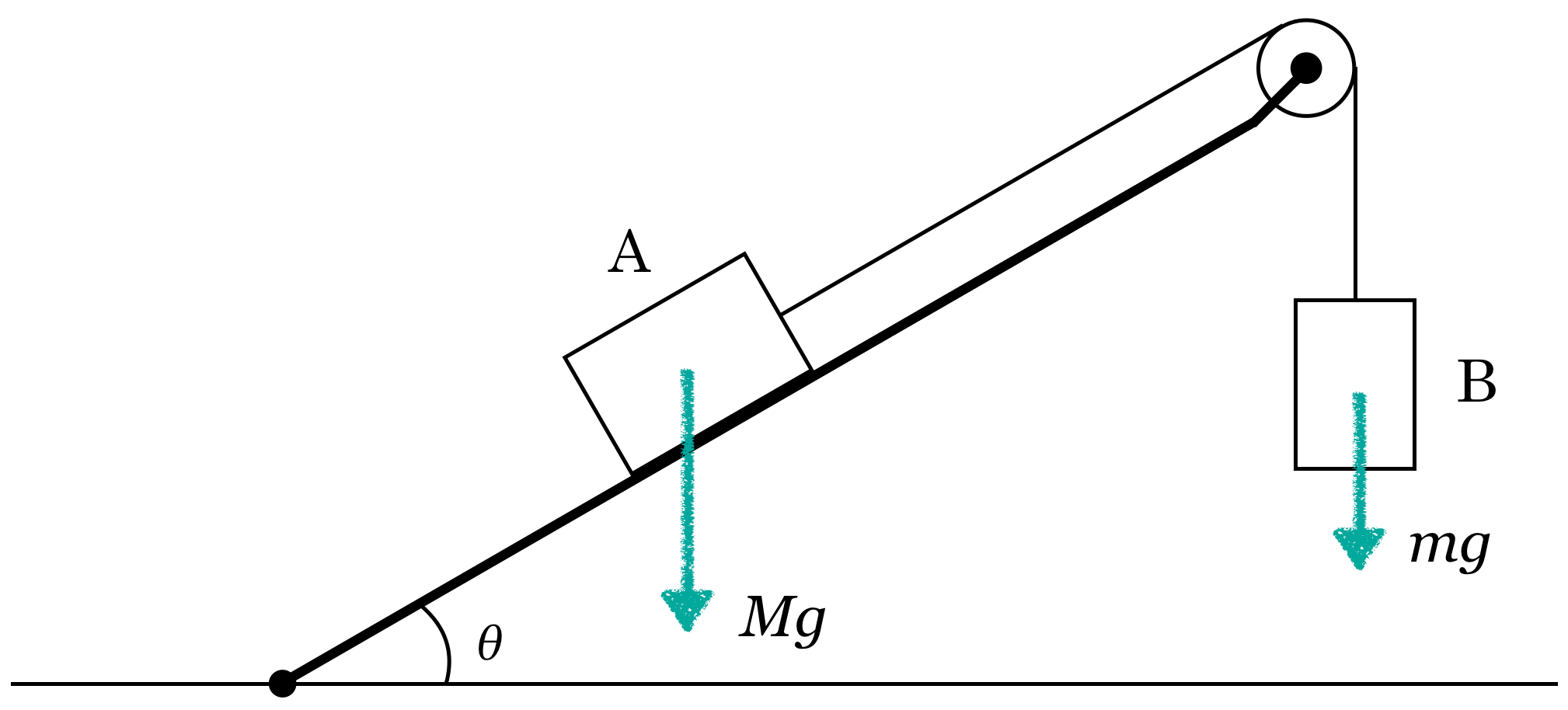
■いきなり質量の比は求められない
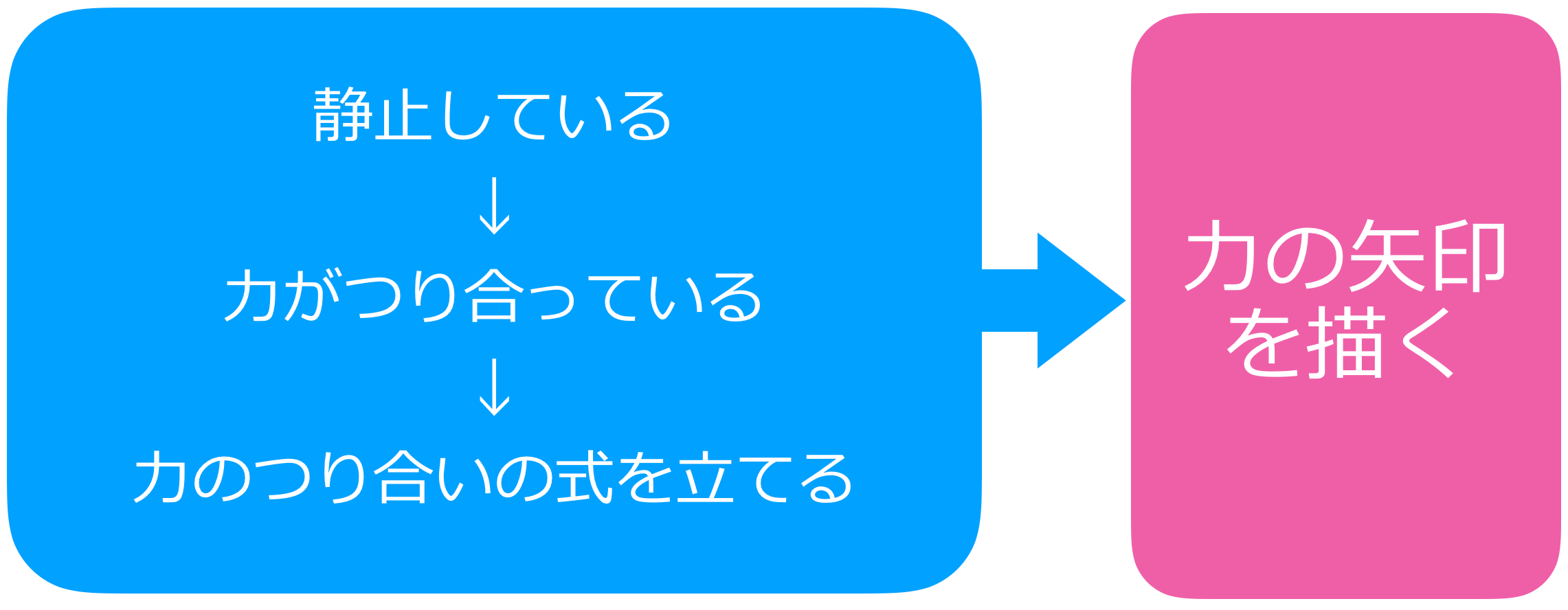
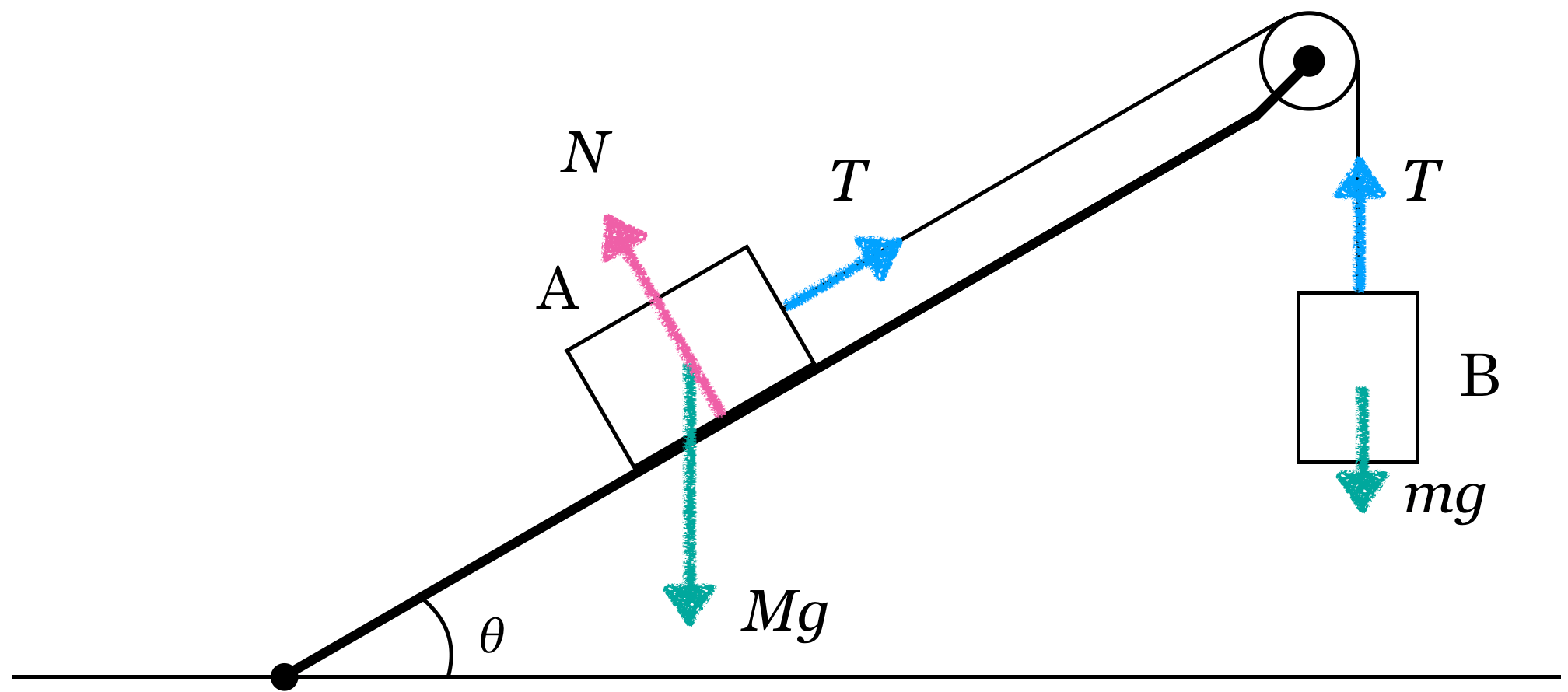
■力の矢印を描く

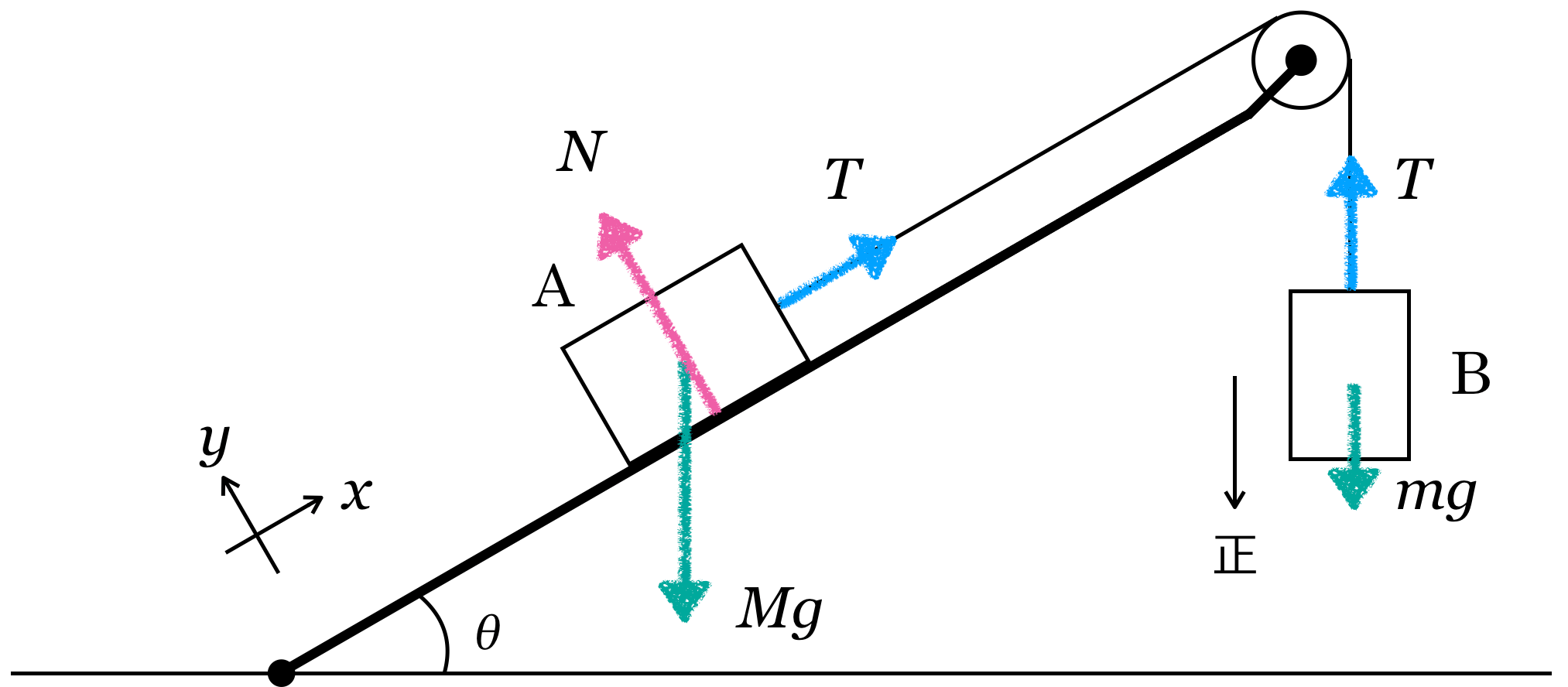
![]() ,糸の張力を
,糸の張力を![]() としたんだね。それでは,次はどうしようか。
としたんだね。それでは,次はどうしようか。

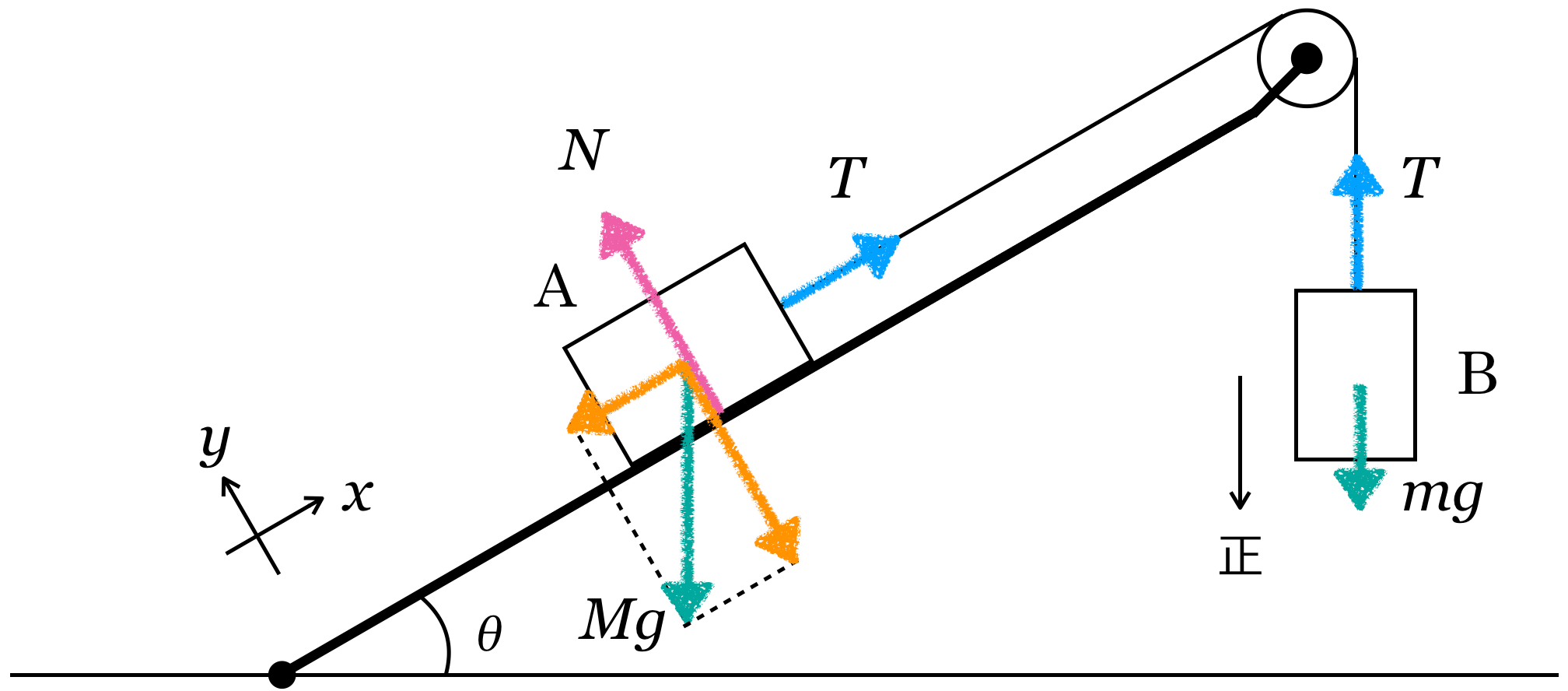
![]() がここだから,こうね。
がここだから,こうね。
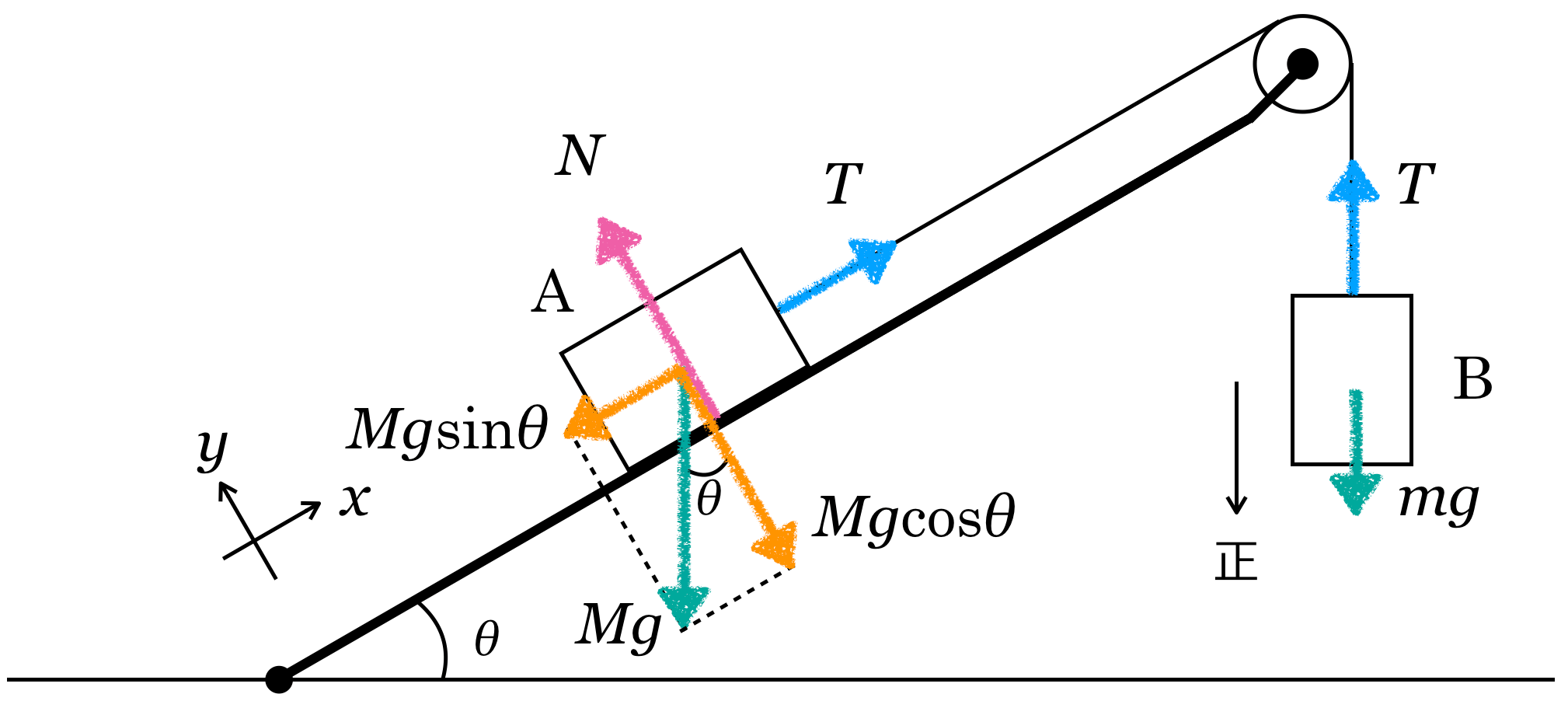
■力のつり合いの式を立てる
物体Aの![]() 方向
方向
![]()
物体Aの![]() 方向
方向
![]()
物体B
![]()
![]() を求められるかな?
を求められるかな?
![]() だけなので,他の文字を消去すればいいわね。
だけなので,他の文字を消去すればいいわね。
![]() の
の![]() はここにしか出てこないので,消去できないのね。ということは,①と③から
はここにしか出てこないので,消去できないのね。ということは,①と③から![]() を消去すればいいのね。
を消去すればいいのね。
①より,
![]()
③に代入
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!




![]() ,糸の張力を
,糸の張力を![]() としたんだね。それでは,次はどうしようか。
としたんだね。それでは,次はどうしようか。



![]() がここだから,こうね。
がここだから,こうね。

物体Aの![]() 方向
方向
![]()
物体Aの![]() 方向
方向
![]()
物体B
![]()
![]() を求められるかな?
を求められるかな?
![]() だけなので,他の文字を消去すればいいわね。
だけなので,他の文字を消去すればいいわね。
![]() の
の![]() はここにしか出てこないので,消去できないのね。ということは,①と③から
はここにしか出てこないので,消去できないのね。ということは,①と③から![]() を消去すればいいのね。
を消去すればいいのね。
①より,
![]()
③に代入
![]()
![]()