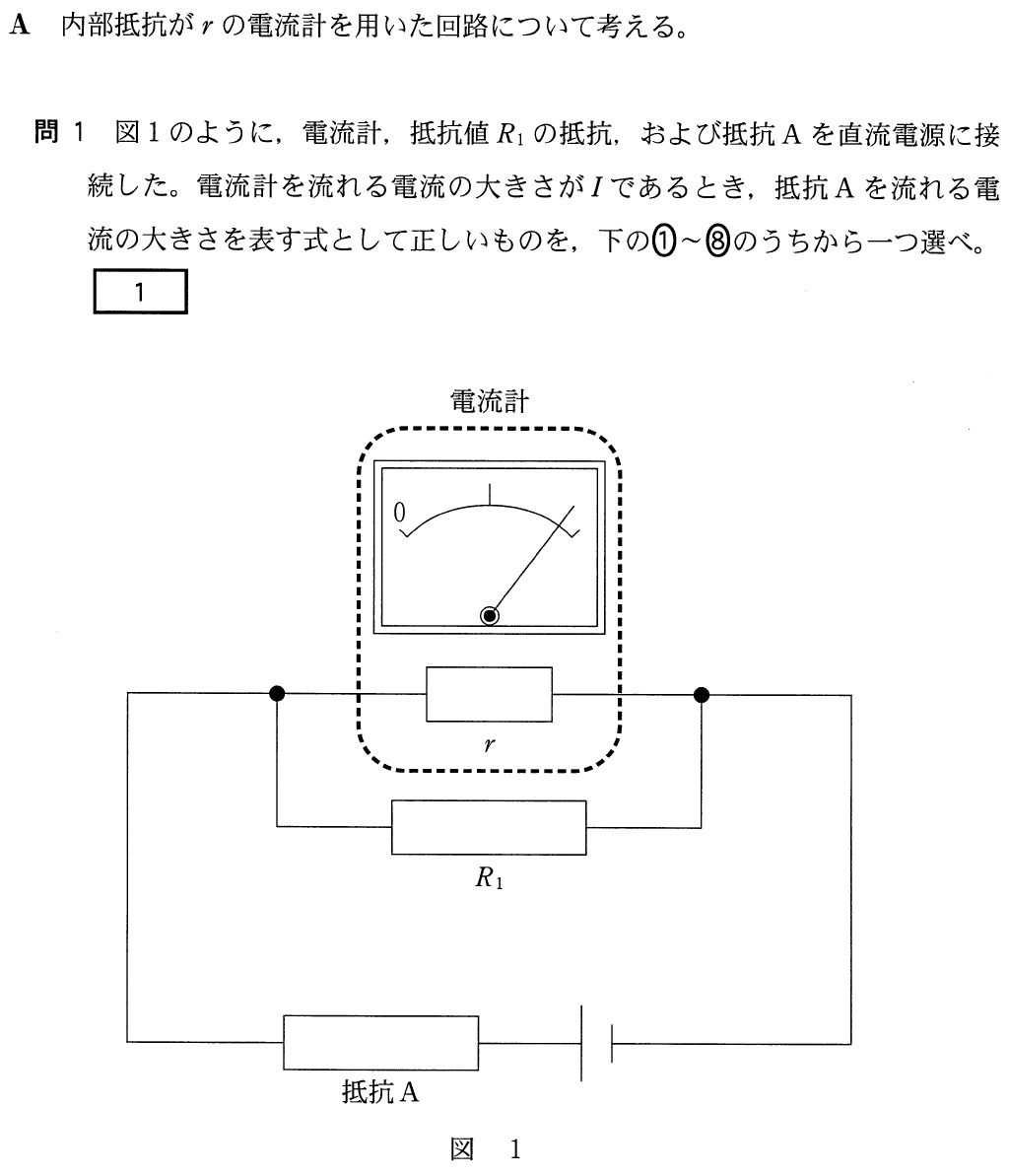
■とにかくオームの法則
電流計の「内部抵抗」って,なんで考えなきゃダメなの?
実際に抵抗があるからね。抵抗がないと電流計の針も動かないんだよ。「内部抵抗」っていう名前にはなってるけど,普通の「抵抗」だと考えればいいから,そんなに難しくはないよ。
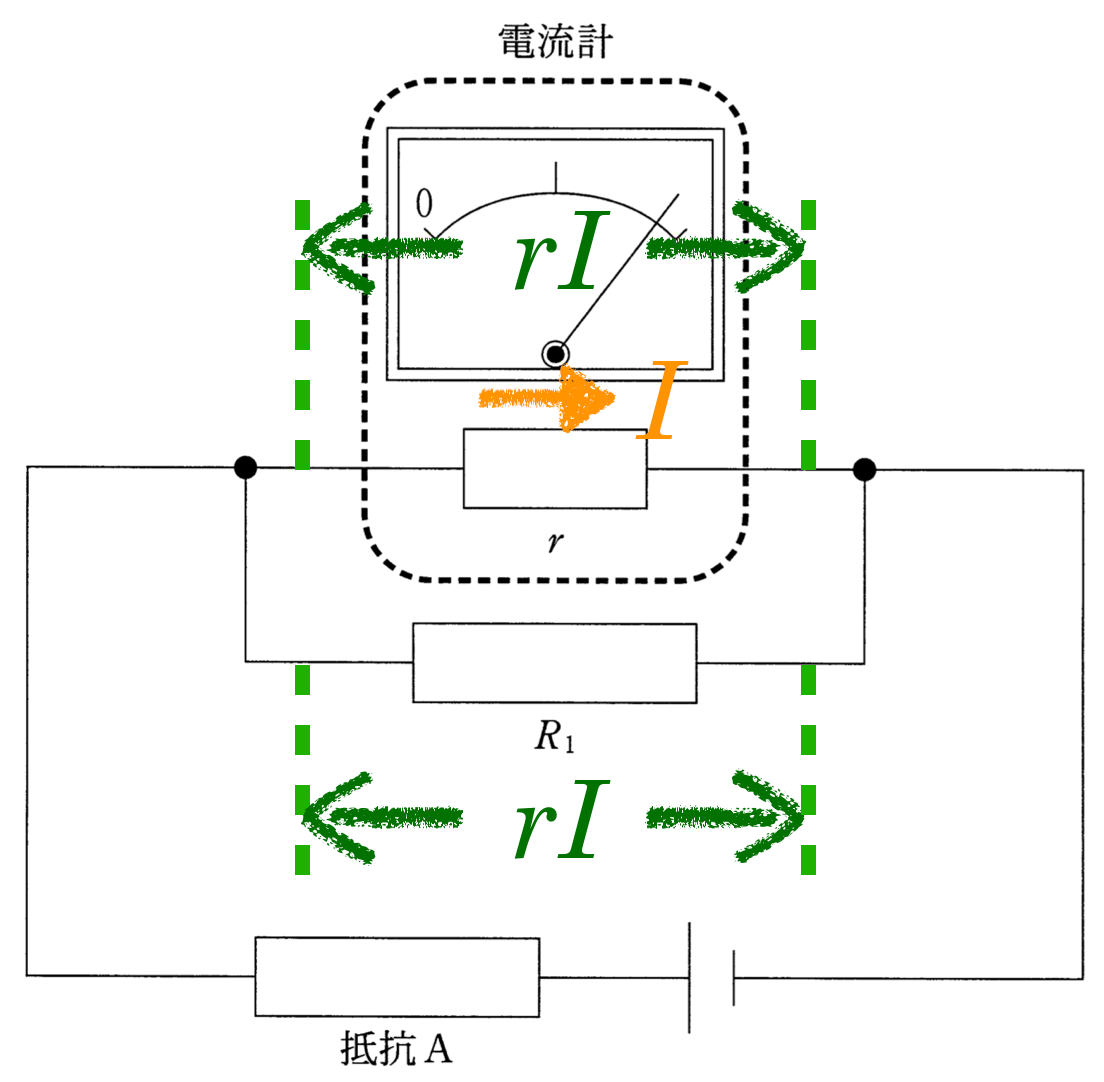
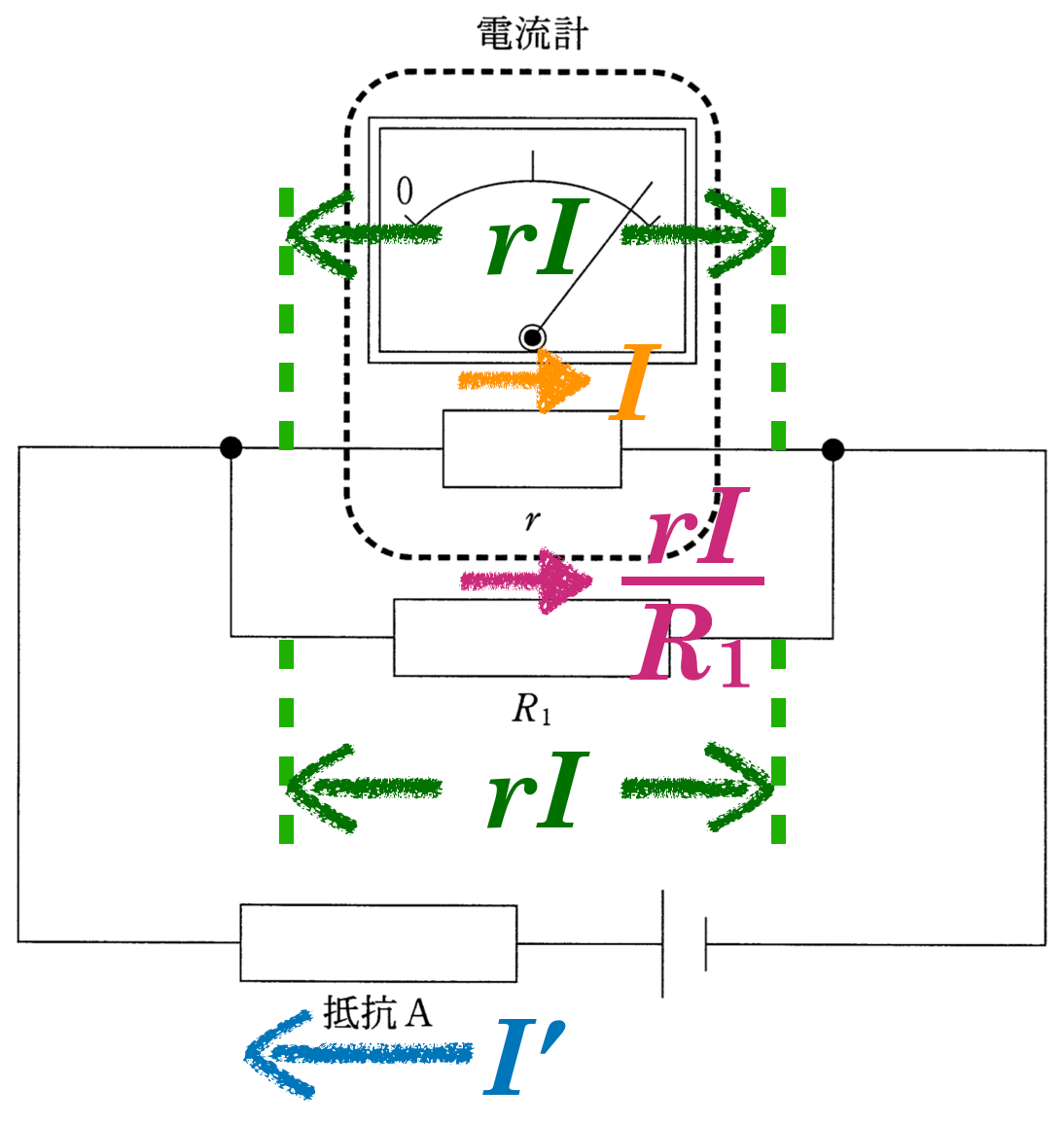
とにかく問題文に書かれている情報を図の中に描き加えていこう。
分かったわ。図に描かれていない情報としては,「電流計を流れる電流の大きさが
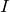
」となっているから,まずは
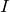
を描いておくわ。流れる向きは右向きでいいわよね。
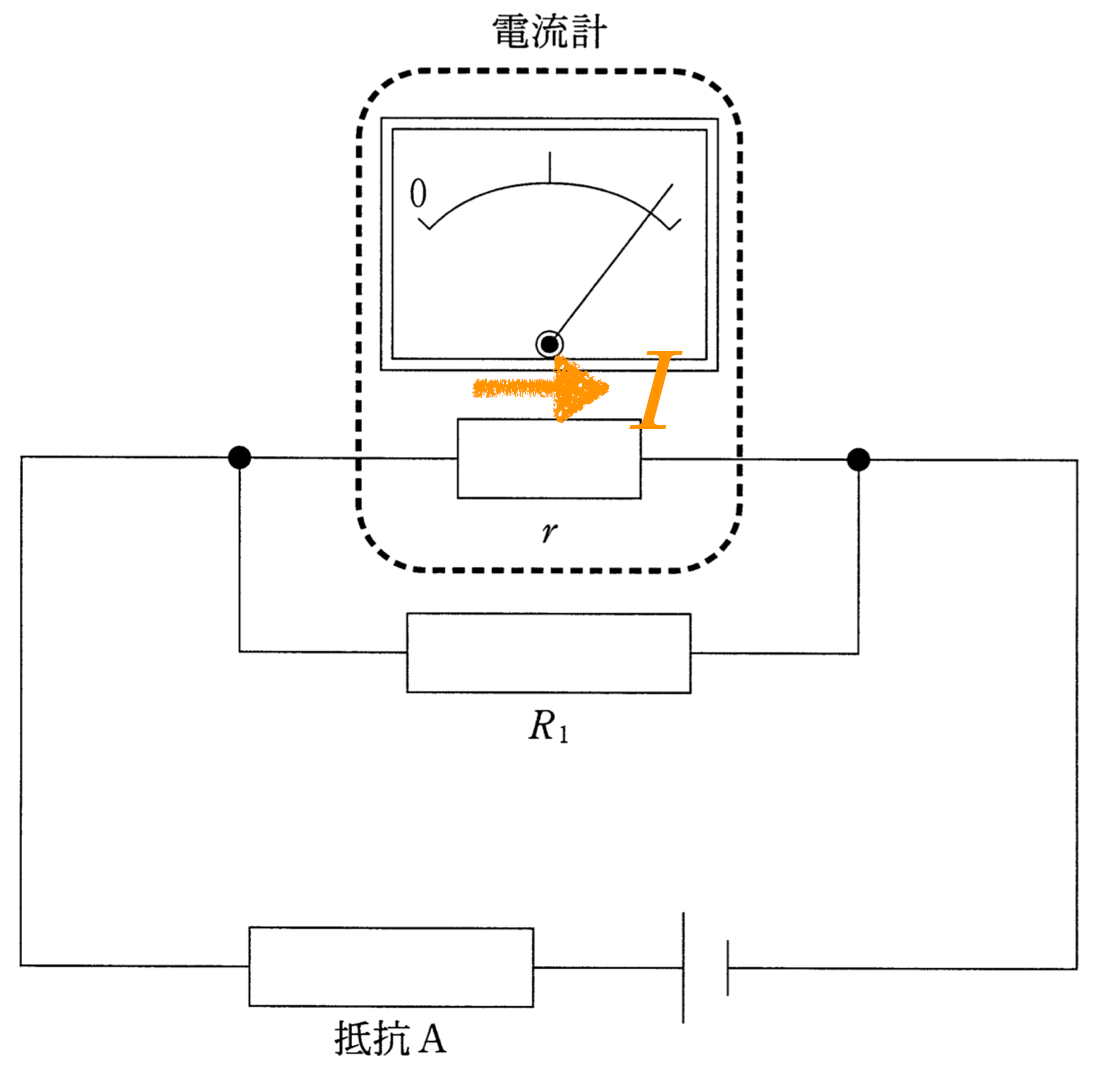
そうだね。下にある電池の向きを考えると,電流計を流れる電流の向きは,右向きだね。そうすると,電流計にかかっている電圧が分かるね。
そうか。内部抵抗が

で,そこを流れる電流の大きさが
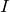
だから,オームの法則を使うのね。

そうすると,電流計の両端の電圧は
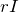
になるわね。
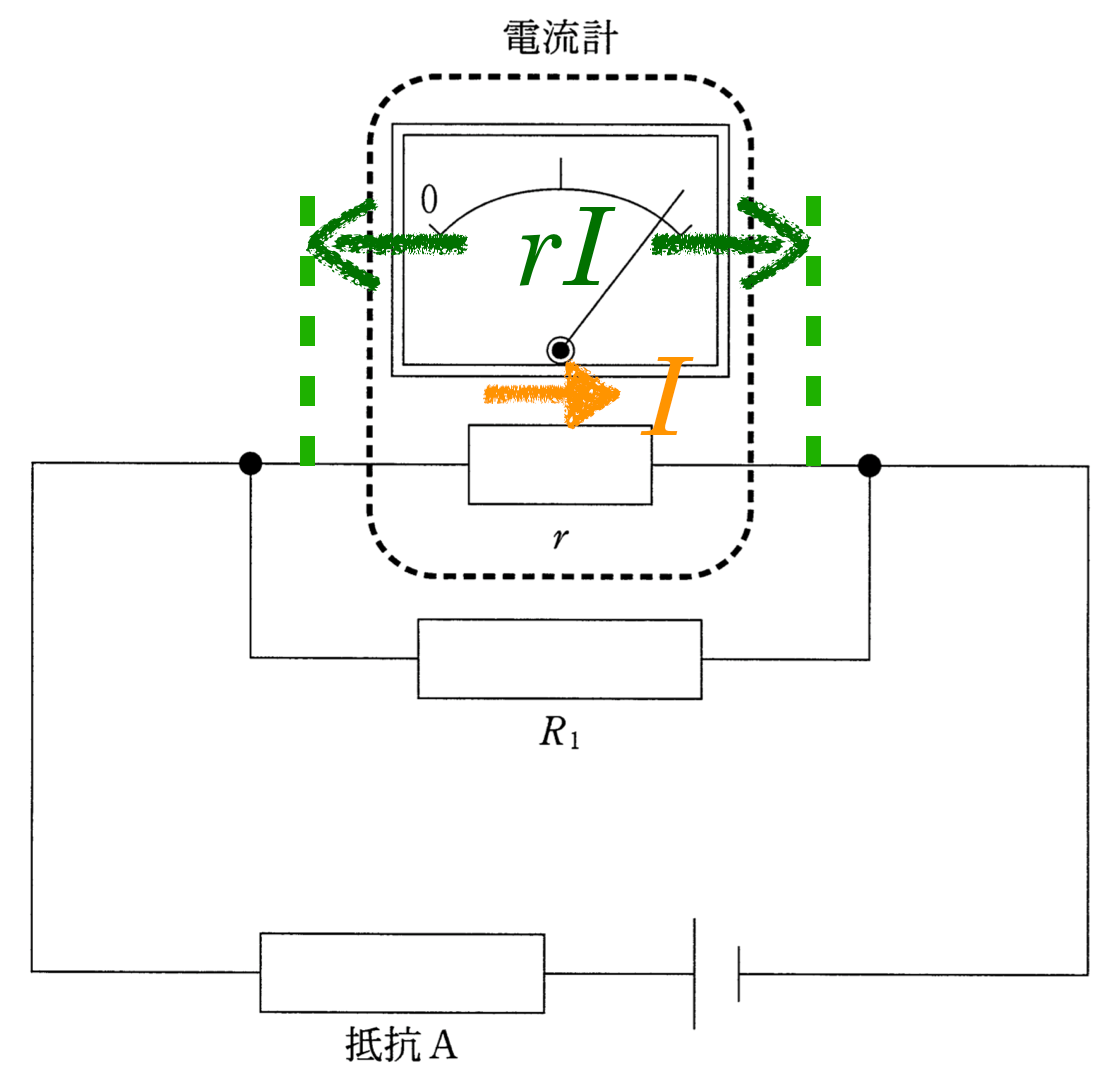
求めたいのは抵抗Aを流れる電流の大きさだけど,まだ求まりそうにないね。次はどうしようか。
真ん中の抵抗って,電流計の内部抵抗と並列だと考えていいの?
そうだよ。電流計の絵が描かれているので,迷うかもしれないけど,電気回路としては,電流計の絵は無視して,単純に2つの抵抗は並列だと考えていいよ。
■並列の場合,電圧は同じ
並列だと,電圧が同じだから,真ん中の抵抗にかかる電圧も
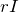
ね。
ということは,真ん中の抵抗を流れる電流も分かるね。
抵抗値が
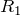
で,電圧が
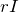
と考えるのね。流れる電流を
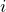
としてオームの法則を使うと,こうよね。
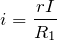
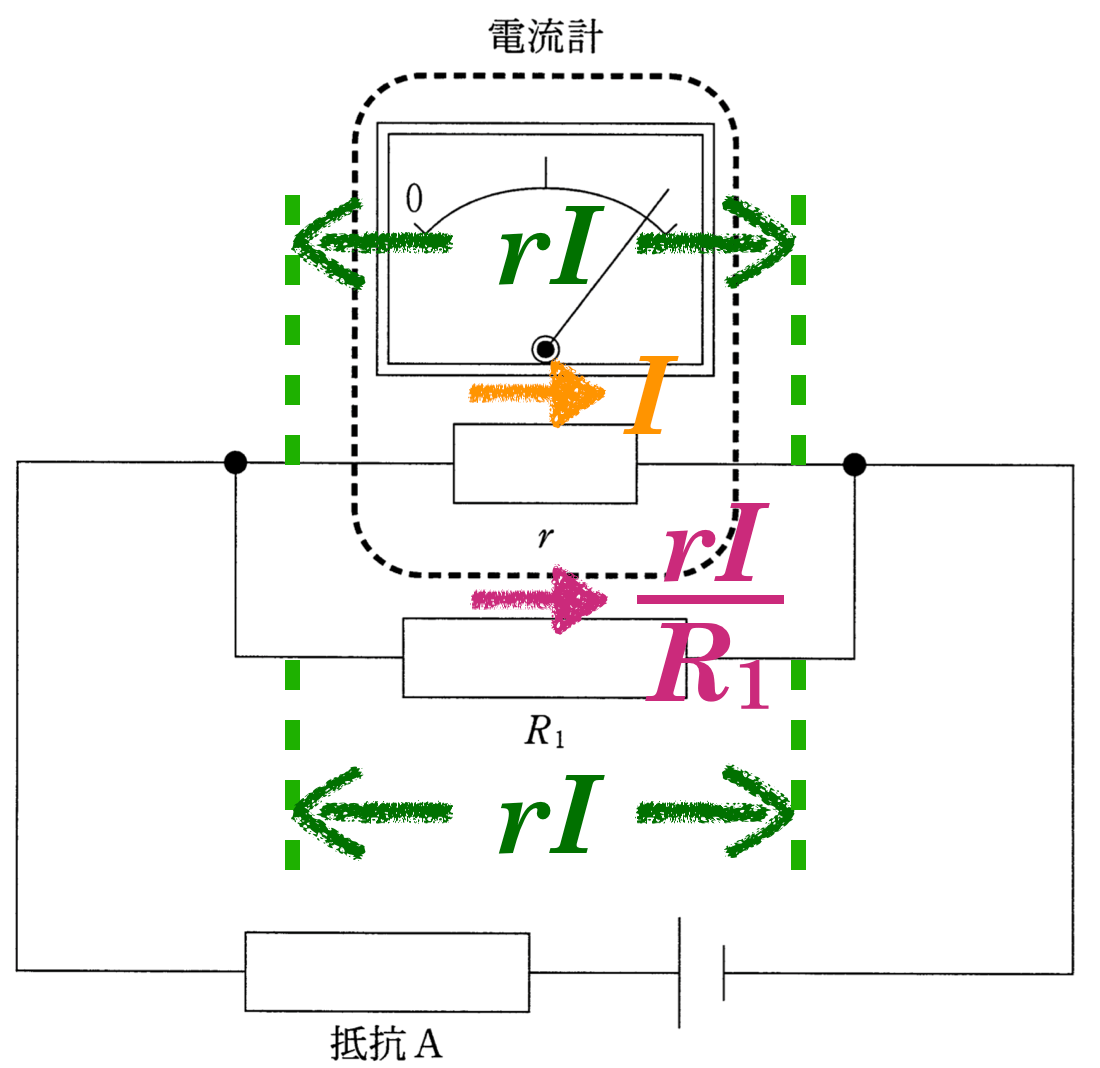
いいね。そうすると,ようやく抵抗Aを流れる電流の大きさ
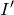
が求められるね。
上の2つの抵抗に流れる電流を合わせたのが,
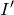
ね。
■問2は問1とほとんど同じ流れで解ける
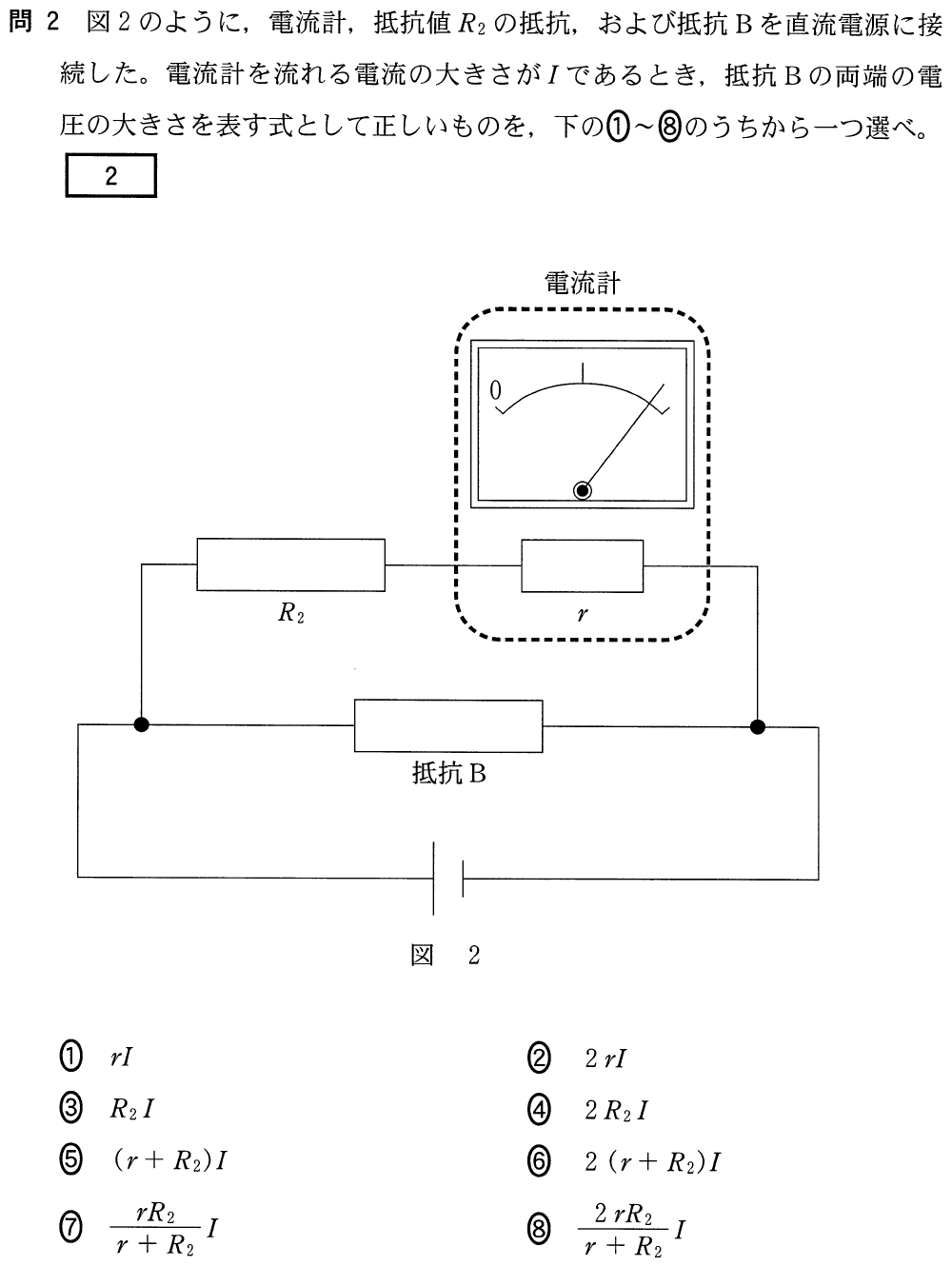
この問題も,問1と同じように考えればいいんじゃないかな。
それじゃあ,まず問題文にある「電流計を流れる電流」を描くわね。
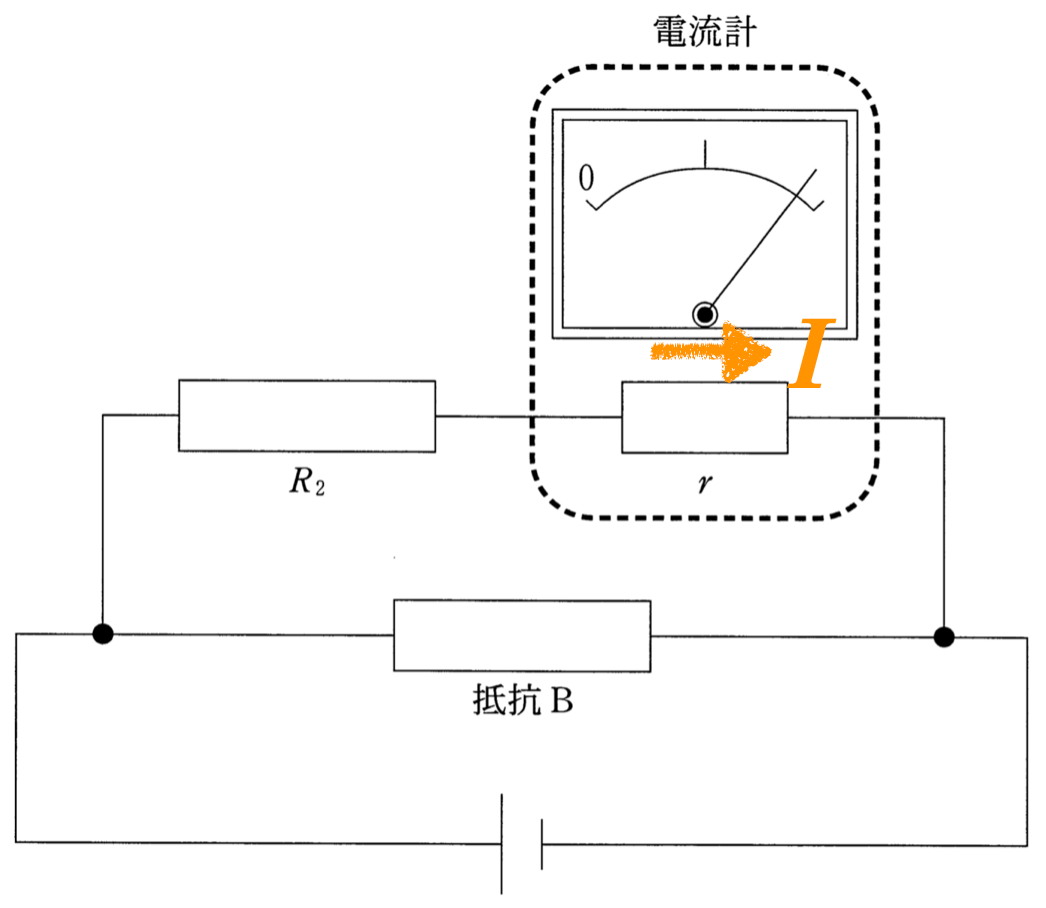
抵抗値と電流の大きさが分かれば,電流計にかかる電圧は,
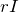
よね。
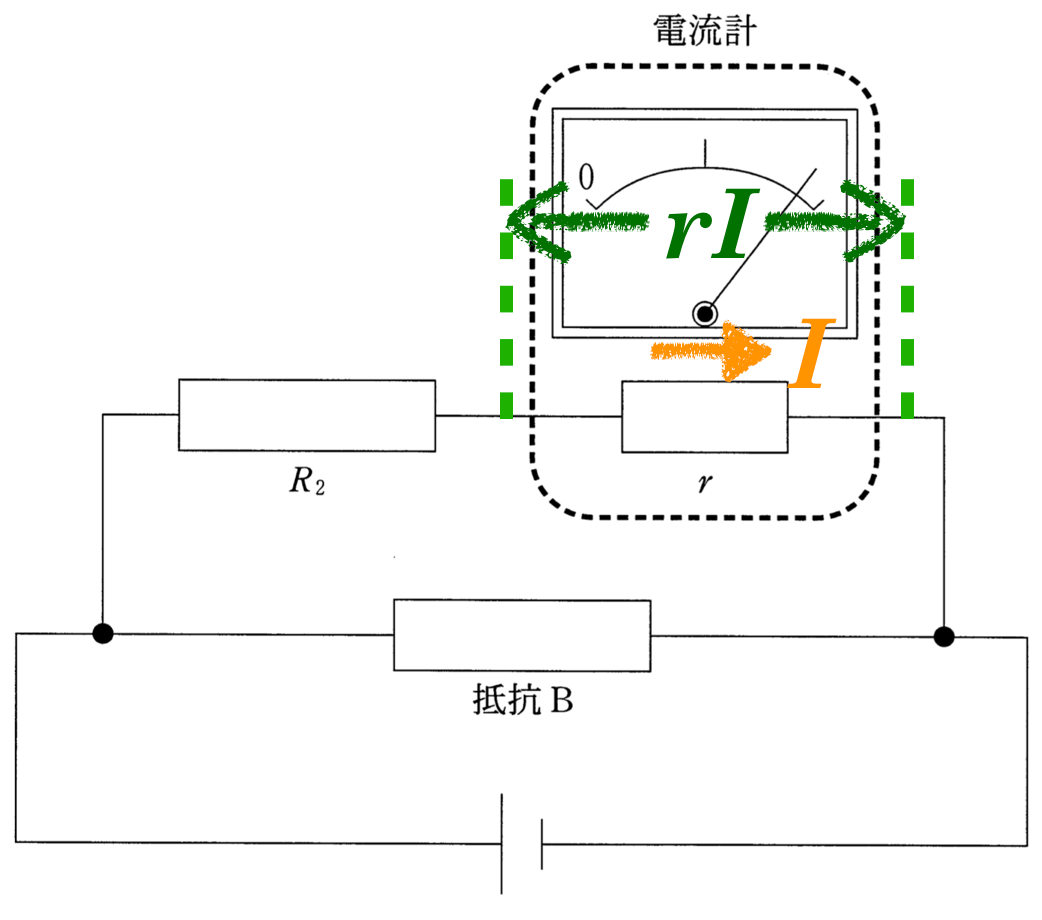
■直列の場合,電流は同じ
今度は,電流計と左上にある抵抗は直列につながっているから,流れる電流は同じよね。
すると,この左上の抵抗にかかる電圧がオームの法則によって
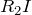
と分かるわね。
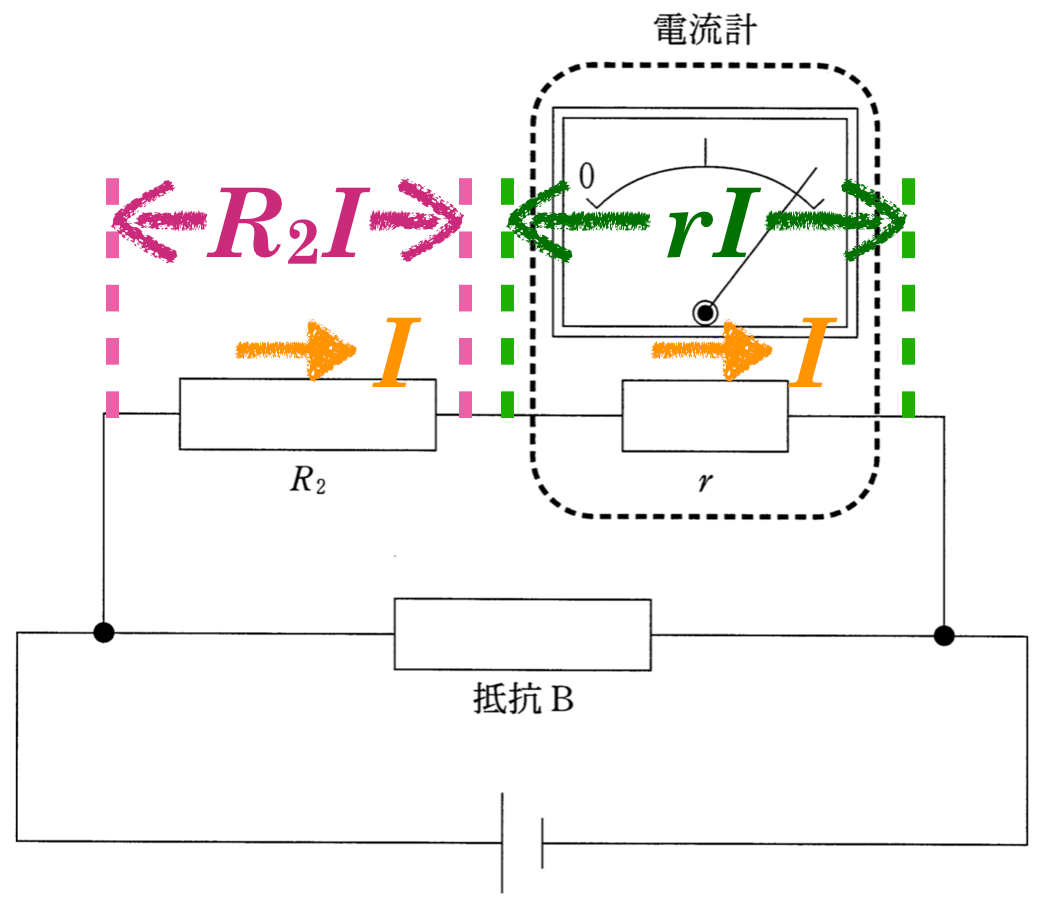
順調だね。今求めたいのは,抵抗Bの両端の電圧の大きさだね。
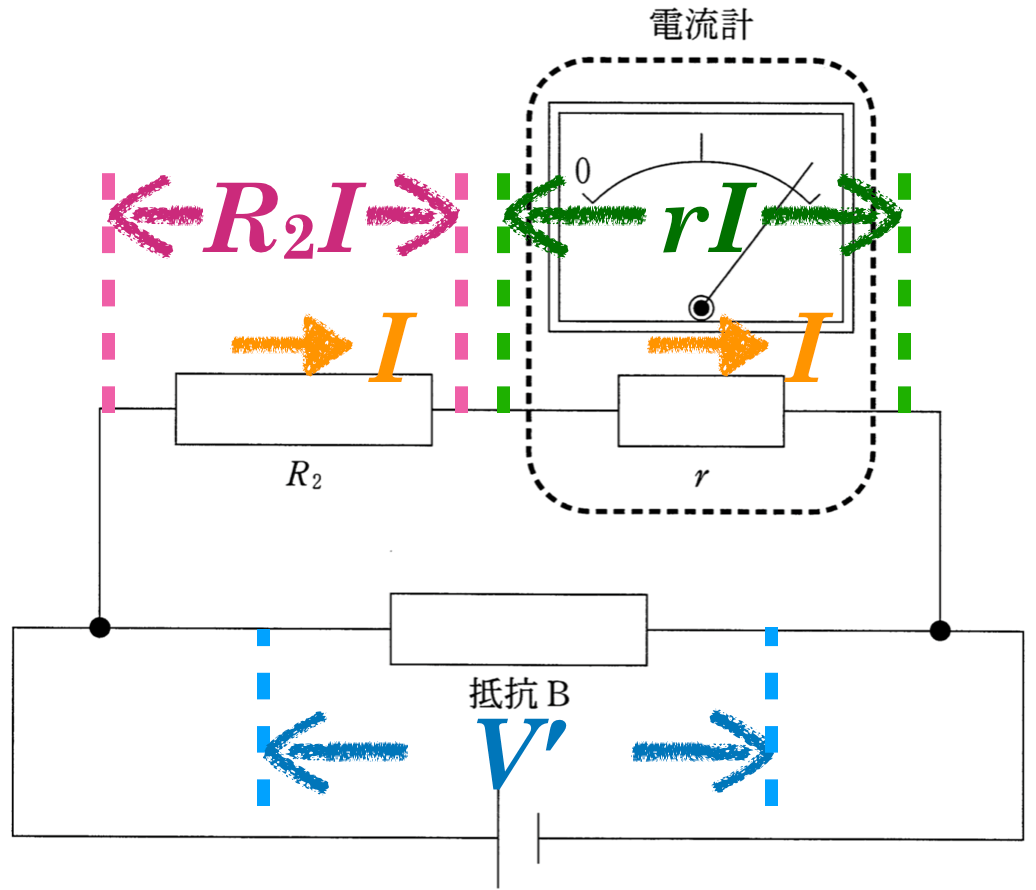
抵抗Bの両端の電圧の大きさを
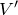
とすると,上の2つの抵抗にかかる電圧の和だから,
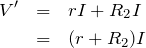

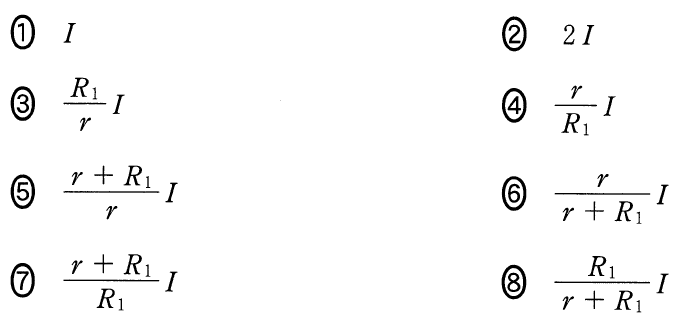
![]() 」となっているから,まずは
」となっているから,まずは![]() を描いておくわ。流れる向きは右向きでいいわよね。
を描いておくわ。流れる向きは右向きでいいわよね。
![]() で,そこを流れる電流の大きさが
で,そこを流れる電流の大きさが![]() だから,オームの法則を使うのね。
だから,オームの法則を使うのね。
![]() になるわね。
になるわね。
![]() ね。
ね。
![]() で,電圧が
で,電圧が![]() と考えるのね。流れる電流を
と考えるのね。流れる電流を![]() としてオームの法則を使うと,こうよね。
としてオームの法則を使うと,こうよね。![]()

![]() が求められるね。
が求められるね。
![]() ね。
ね。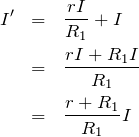


![]() よね。
よね。

![]() と分かるわね。
と分かるわね。

![]() とすると,上の2つの抵抗にかかる電圧の和だから,
とすると,上の2つの抵抗にかかる電圧の和だから,![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
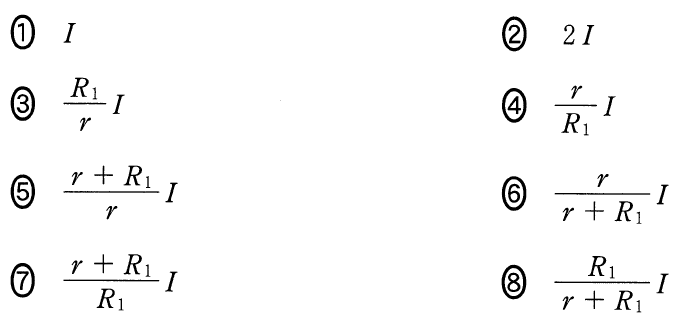
![]() 」となっているから,まずは
」となっているから,まずは![]() を描いておくわ。流れる向きは右向きでいいわよね。
を描いておくわ。流れる向きは右向きでいいわよね。
![]() で,そこを流れる電流の大きさが
で,そこを流れる電流の大きさが![]() だから,オームの法則を使うのね。
だから,オームの法則を使うのね。
![]() になるわね。
になるわね。
![]() ね。
ね。
![]() で,電圧が
で,電圧が![]() と考えるのね。流れる電流を
と考えるのね。流れる電流を![]() としてオームの法則を使うと,こうよね。
としてオームの法則を使うと,こうよね。![]()

![]() が求められるね。
が求められるね。
![]() ね。
ね。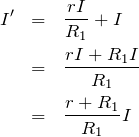


![]() よね。
よね。

![]() と分かるわね。
と分かるわね。

![]() とすると,上の2つの抵抗にかかる電圧の和だから,
とすると,上の2つの抵抗にかかる電圧の和だから,![]()