■臨界角とは
屈折の問題ね。屈折の法則を使うと思うんだけど，どこから手を付けていいか分からないわ。
キーワードとしては，まず「臨界角」かな。「臨界角」って何だろう？
確か「全反射」の話の時に出てきたと思うんだけど･･･
「全反射」の手前っていうか，入射角が「臨界角」を超えると「全反射」になるんだよね。
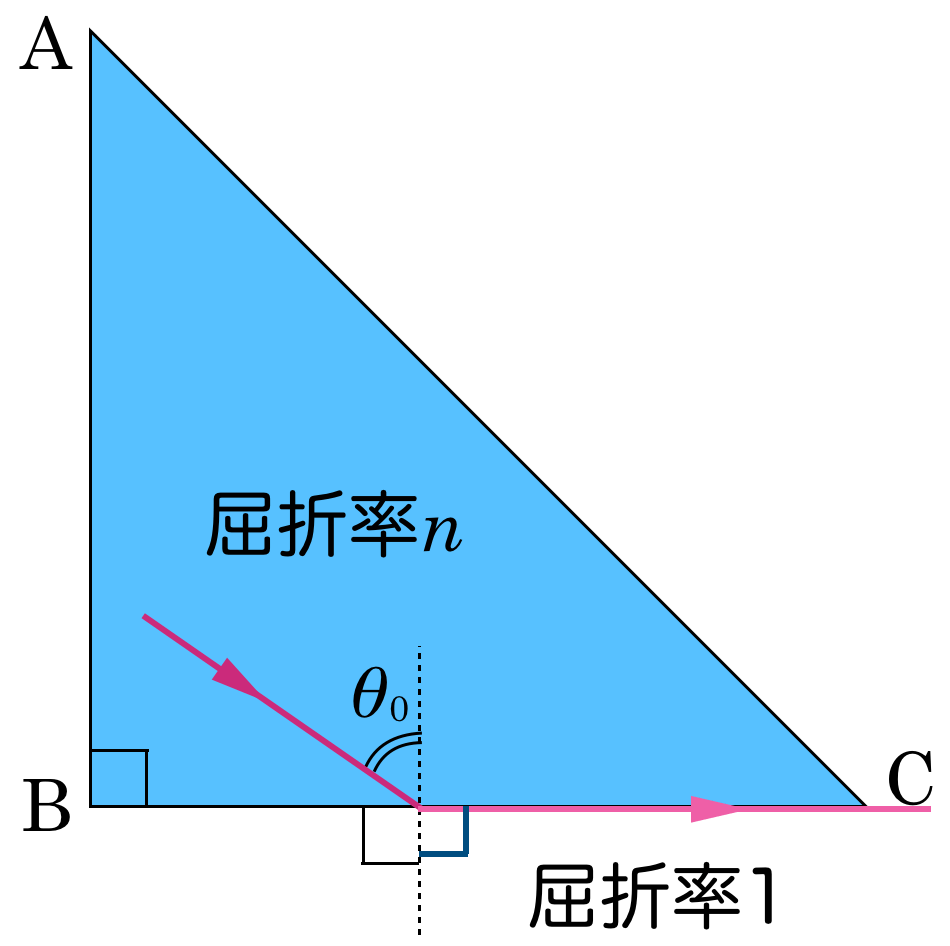
「臨界角」がポイントなので，先に面BCでの屈折から考えてみようか。面BCに入る光の入射角を小さくしてみると，屈折して出ていく光はどう進むかな？
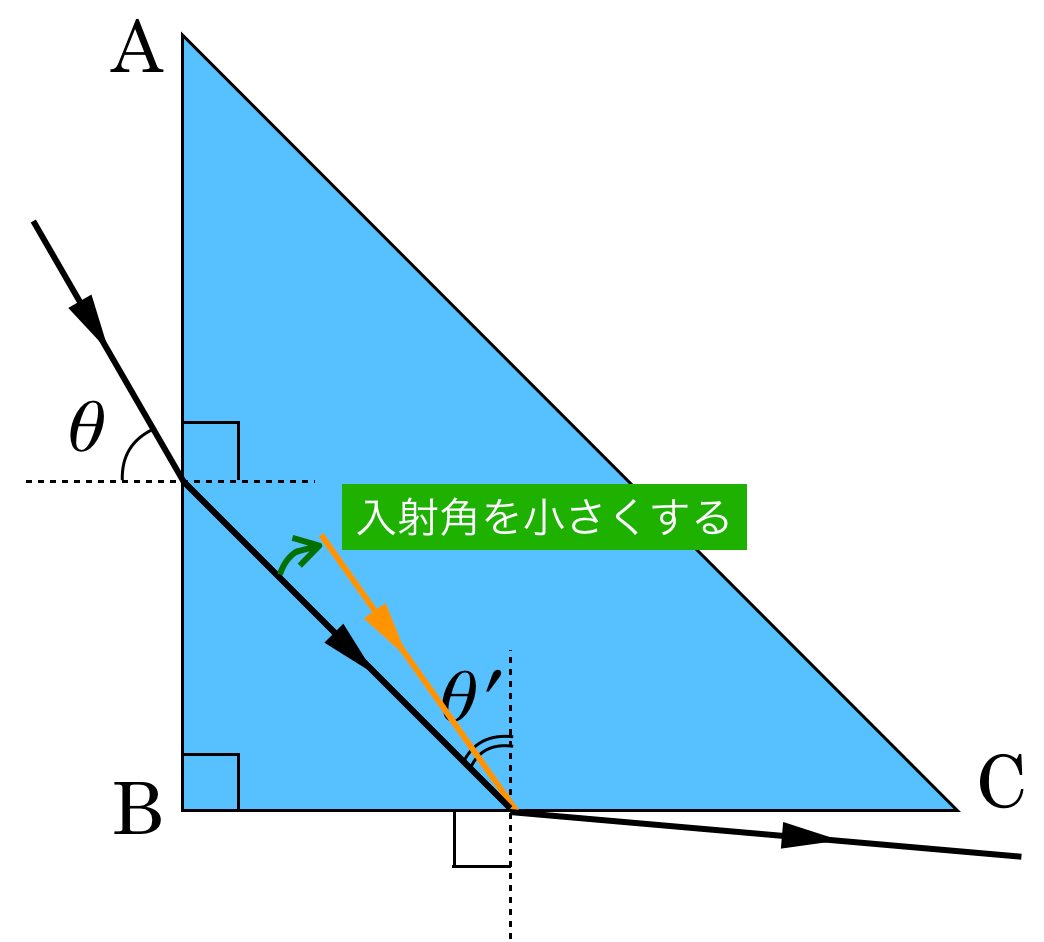
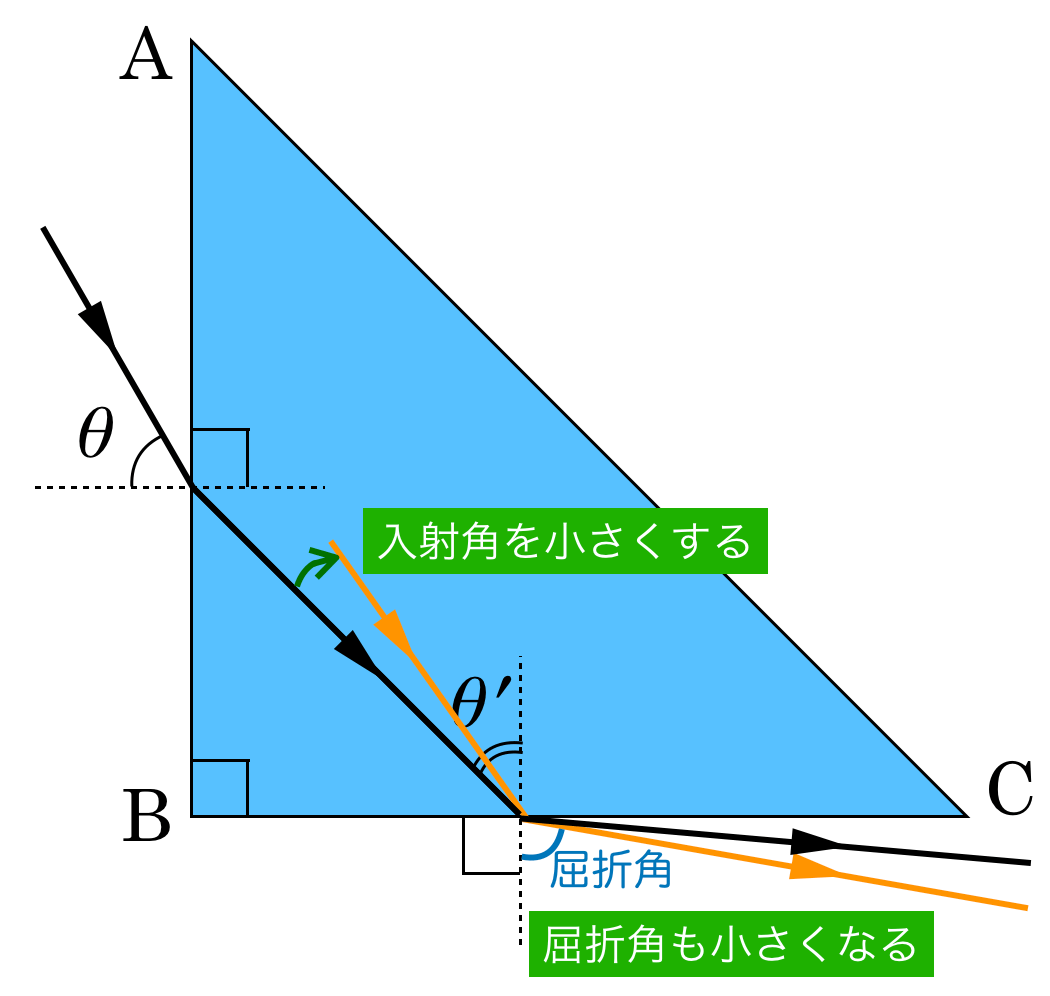
そうだね。面BCの鉛直線と出ていく光の方向のなす角を屈折角というけど，入射角を小さくすると，屈折角も小さくなるんだよね。屈折する方向は感覚的にも分かると思うけど，屈折の法則を考えても，角度の大小は分かるね。
ということは，面BCにおける入射角をいくら小さくしても，屈折角が90°にはなりそうもないわね。
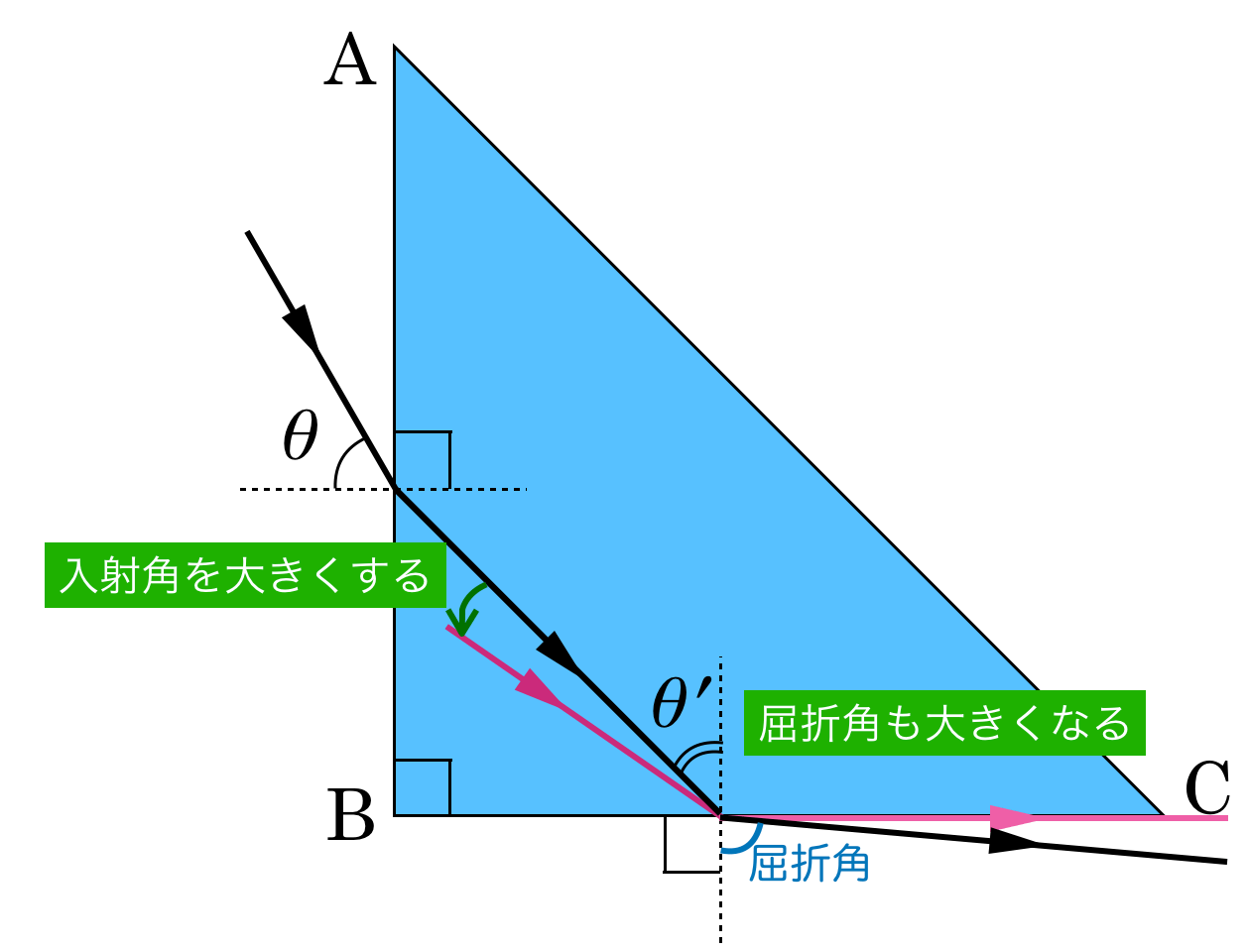
そして，屈折角が90°になるときの入射角を「臨界角」っていうんだ。
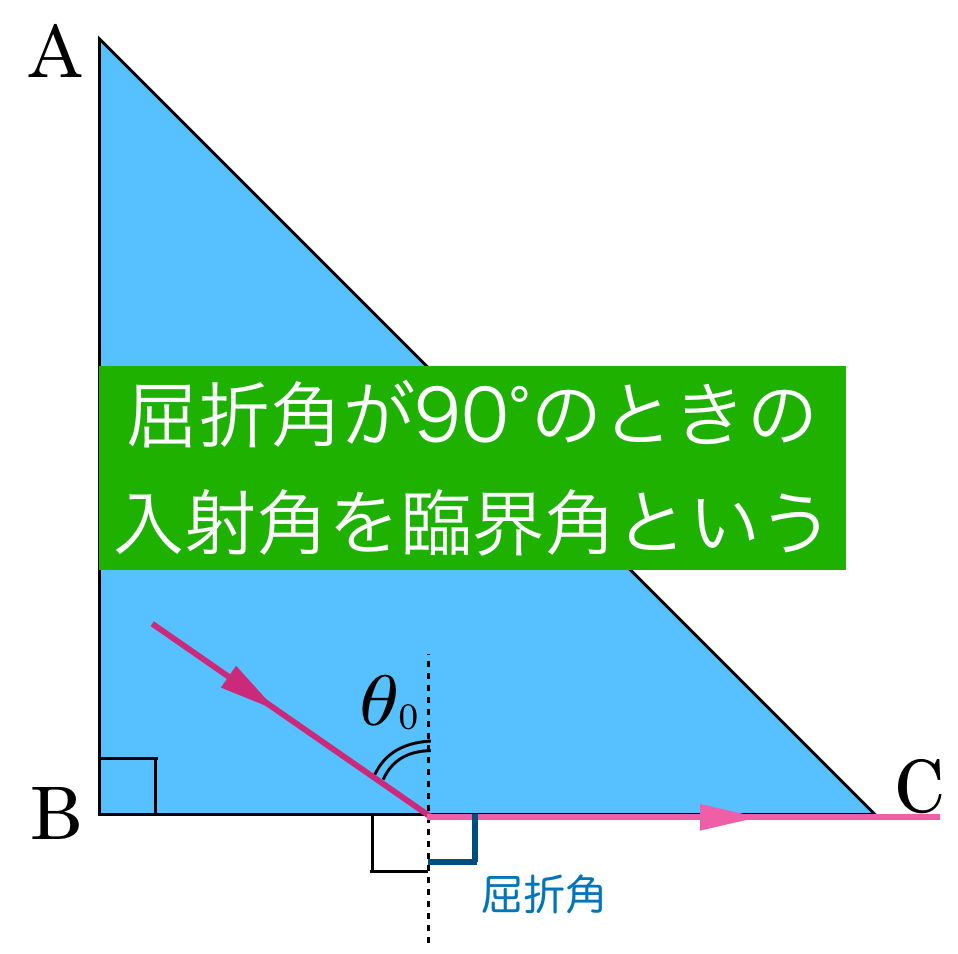
ということは，入射角が大きくなると「臨界角」になるのね。
その通りなんだけど，あくまでも今考えていたのは面BCにおける入射角ね。
そうか。今，求めたいのは面ABにおける入射角なのね。
■面ABにおける屈折の図を描く
なので，次は面ABにおける屈折の様子を描いてみようか。
入射角を大きくするときと，小さくするときを同時に描いてみるわ。
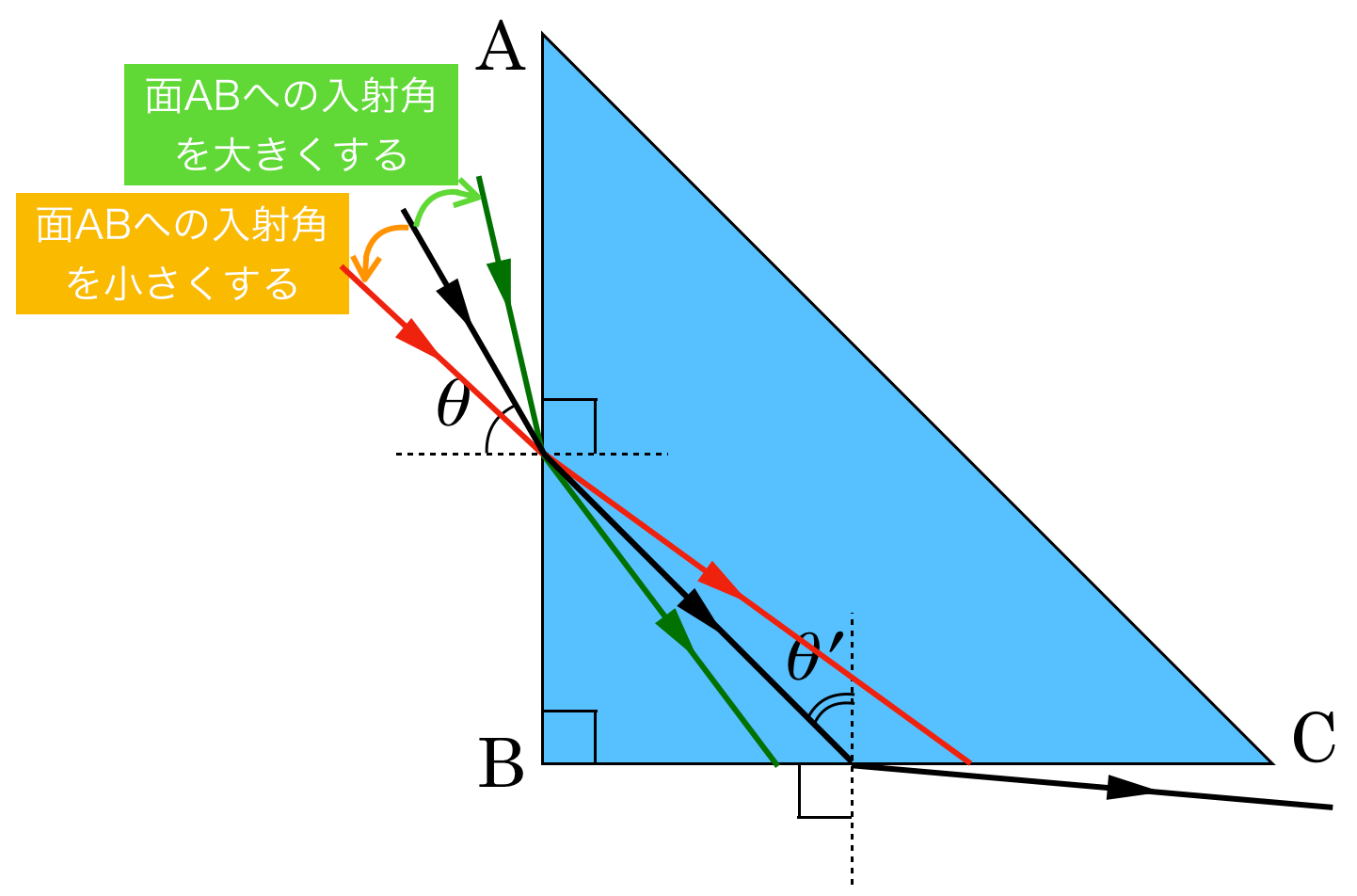
そんな感じだね。そうすると，求めたいのはどっちかな？
求めたいのは面BCにおける入射角が大きくなる方だから，えっと，どっちかな？
面BCに入射する場所が変わっちゃったから，分かりにくくなっちゃったかな？面BCに垂線を描いてみたら？
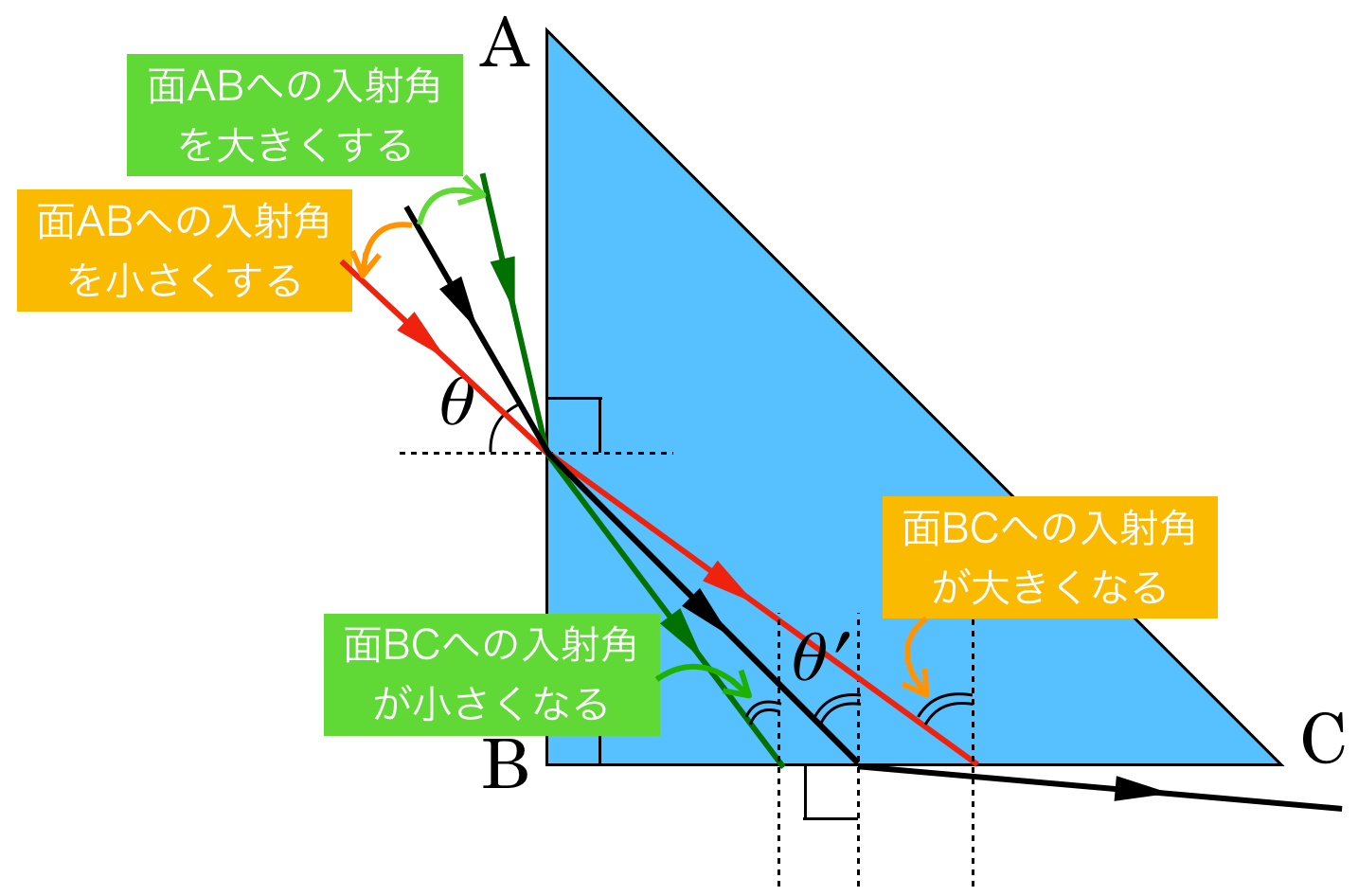
そうすると，右に来ている方が面BCへの入射角が大きくなっているわね。ということは，まとめるとこういうことね。
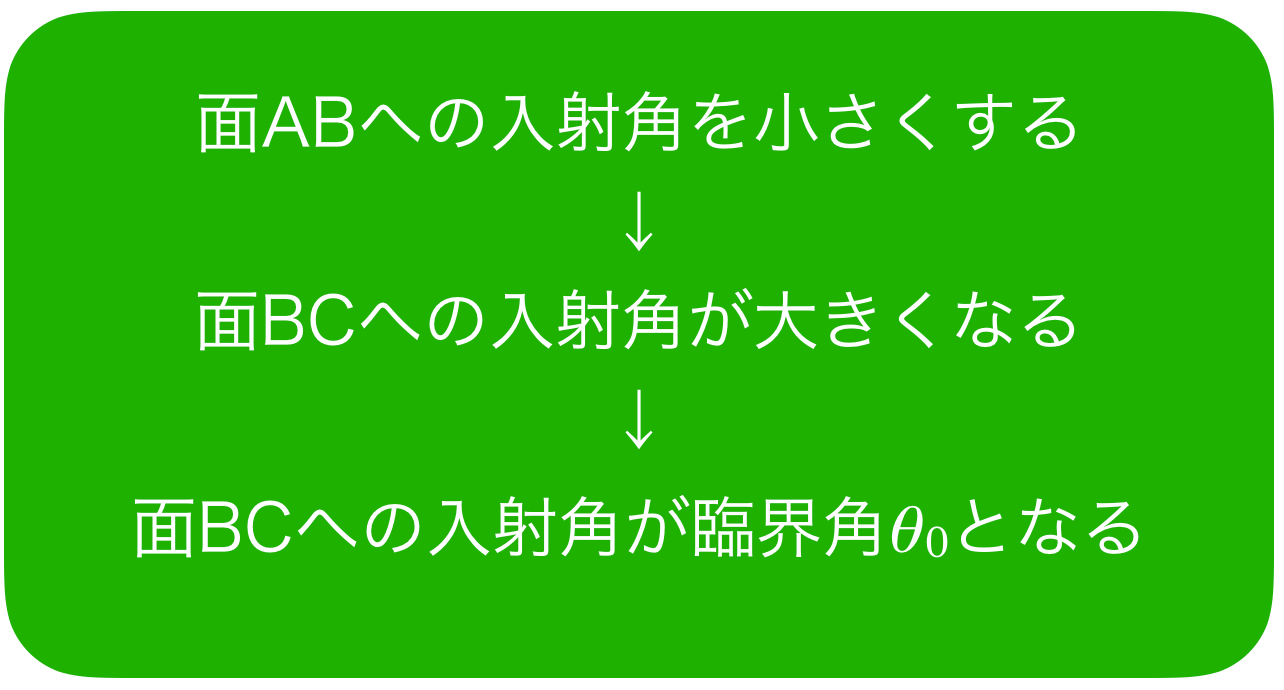
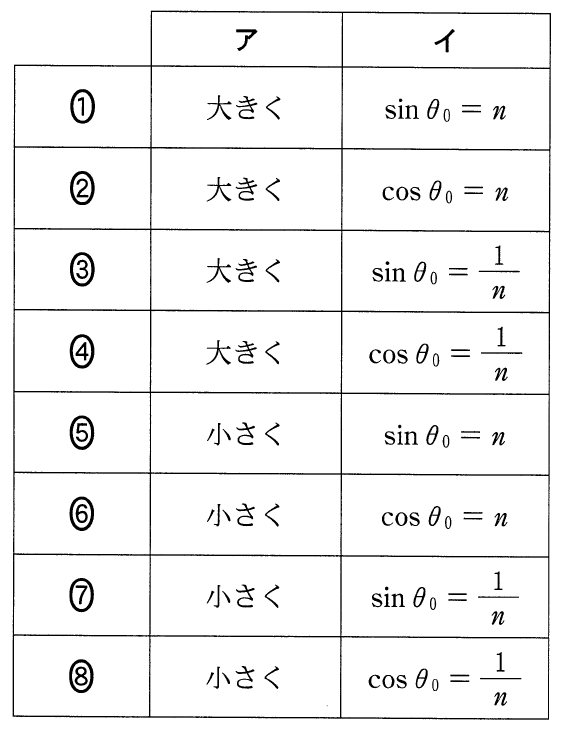
そうだね。最初の空欄アには「小さく」が入るね。次の空欄はどうかな？
■屈折の法則の使い方
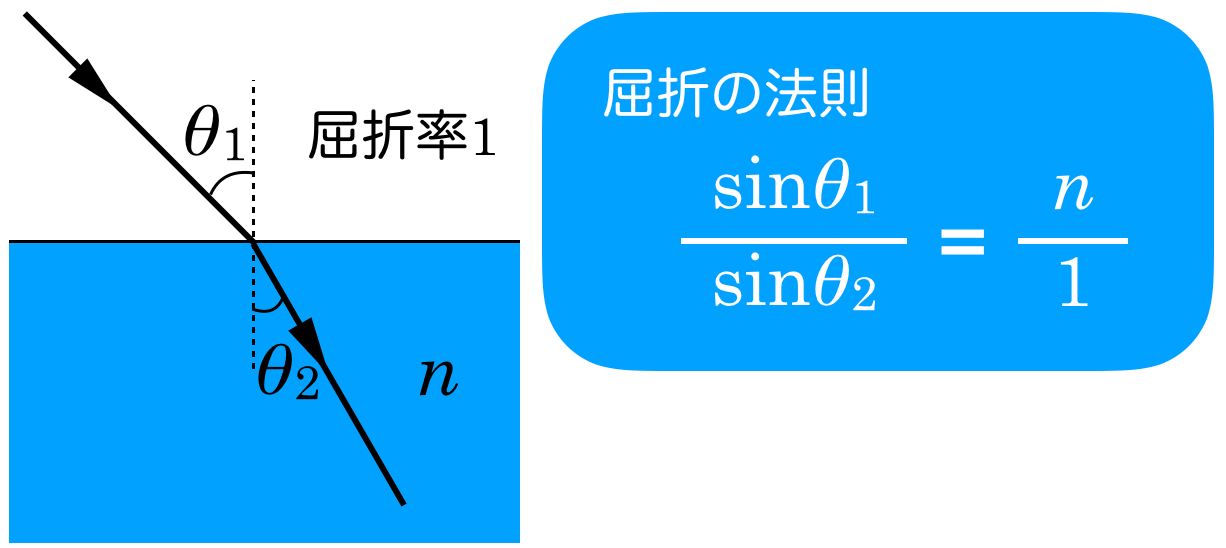
そうだね。屈折の法則をまとめておくよ。次の図のように２つの媒質があって，入射角（屈折角），速さ，波長，屈折率の関係が次のようになるんだね。
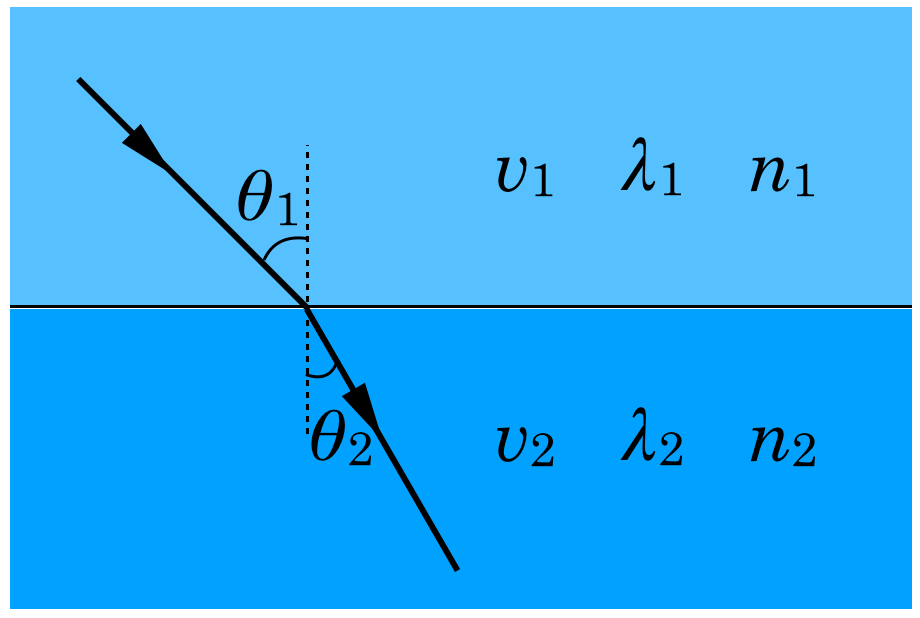
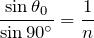
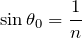
正解だ。答えは⑦だね。それじゃあ問２に行ってみよう。
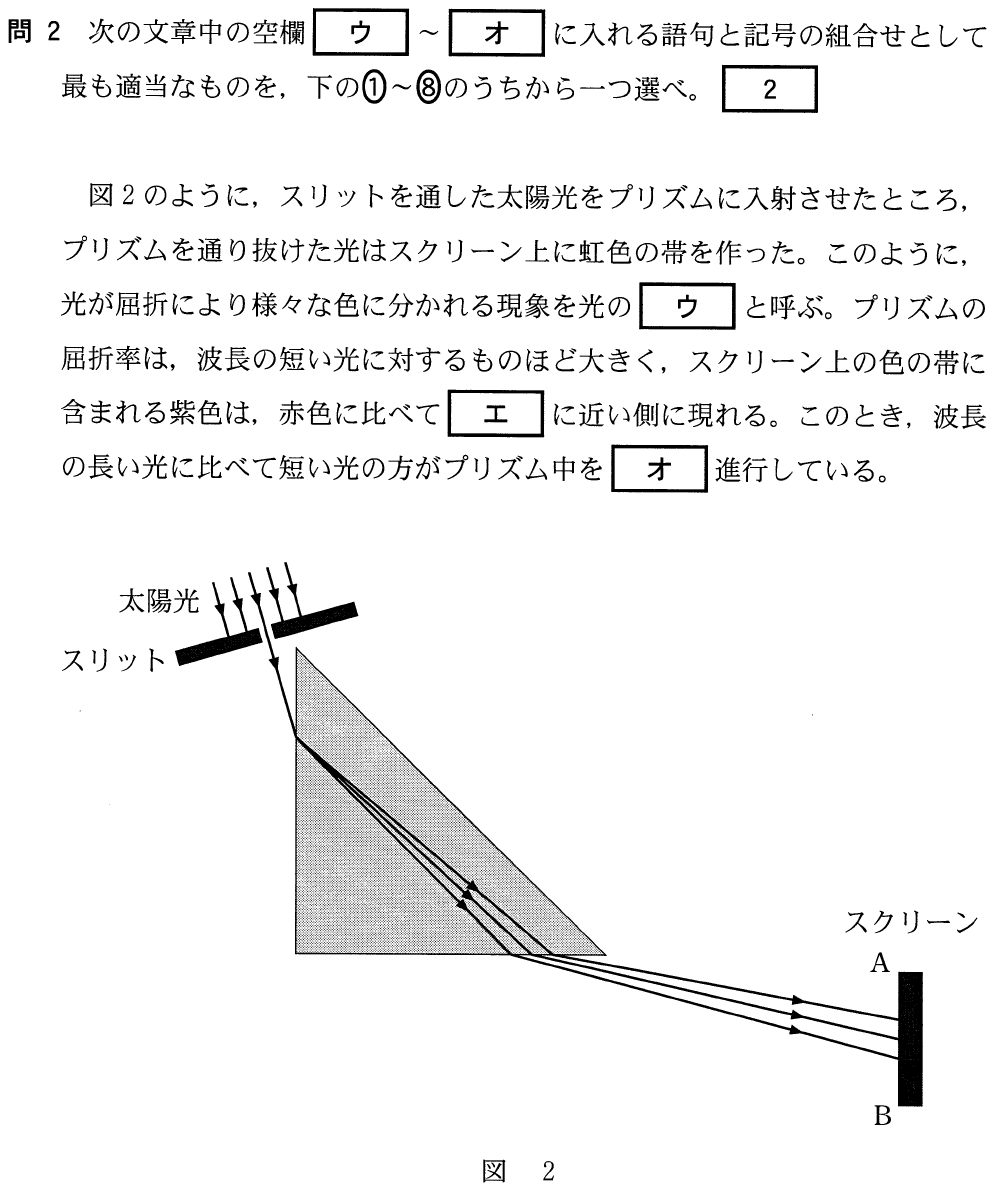
■「分散」と「回折」
選択肢を見ると最初の空欄は，「分散」か「回折」ね。
「分散」も「回折」も図を描くと波が広がっていく感じにはなるけど，現象は全然違うよね。
そうだね。「回折」は，教科書などでは波の様々な分野で具体的な例が紹介されていて，防波堤による海の波の回折，塀などによる音の回折，山や建物による電波の回折，そして回折格子による光の回折などがあるね。
「分散」は，たくさんの振動数（波長）の混ざった波が，媒質の振動数（波長）に対する屈折率の違いで分けられる現象なんだけど，普通は光の分散しか出てこないね。この問題のようなプリズムによる光の分散や，虹ができる仕組みのところで出てくるくらいかな。
ということは，この問いの答えは「分散」ということ？
そう，空欄ウの答えは「分散」だ。詳しいことは問題文の続きを読むと分かるよ。
■屈折率は，波長によって変わる
「プリズムの屈折率は，波長の短い光に対するものほど大きく」って書いてあるけど，屈折率って大きくなったり小さくなったりするの？物質によって決まっている値じゃないの？そもそもこの問題の問１にも「屈折率
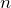
のプリズム」って書いてあるわよ。
そうだね。屈折率は物質によって決まっている値だよ。例えば，こんな値だよ。
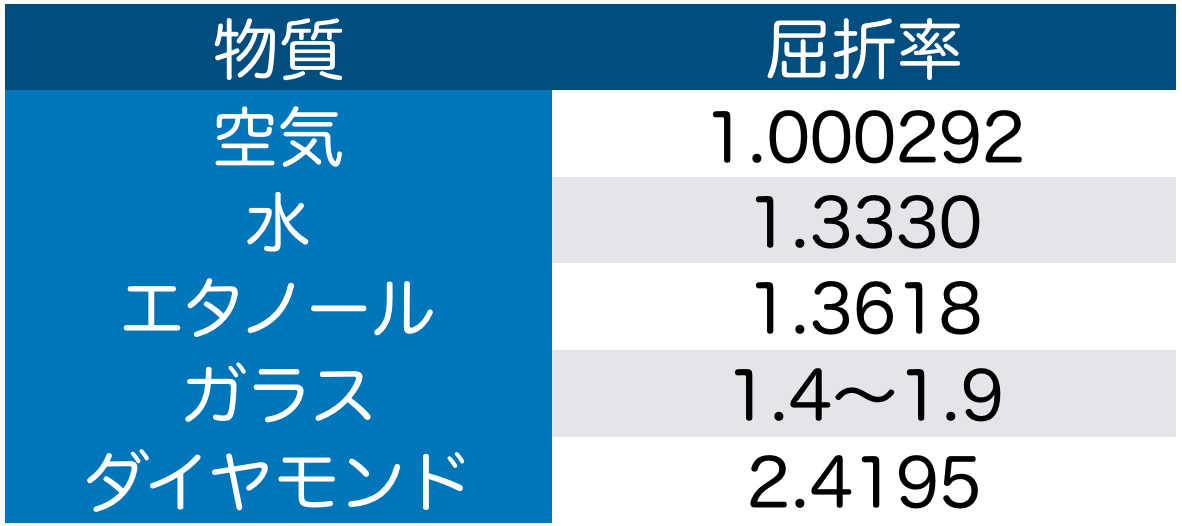
ガラスって，いろんな種類があるので，屈折率も様々な値があるということなんだ。でもだいたい１.4〜1.9の間に収まるんだね。
そうなんだ。ナトリウムランプって，トンネルのオレンジ色の光なんだけど，最近のトンネルはナトリウムランプを使わなくなっているので，だいぶん減っちゃったからあんまり見ないかな？
なんとなくわかるわ。オレンジ色のトンネル。その色の光の屈折率が，さっきの表っていうこと？
そういうことなんだ。逆に言うと，違う波長の光だと，屈折率も変わるということだね。どう変わるかというと，この問題の文章のように，「屈折率は，波長の短い光に対するものほど大きく」なるんだ。
そう，赤の方が波長が長くて，紫の方が波長が短いんだね。
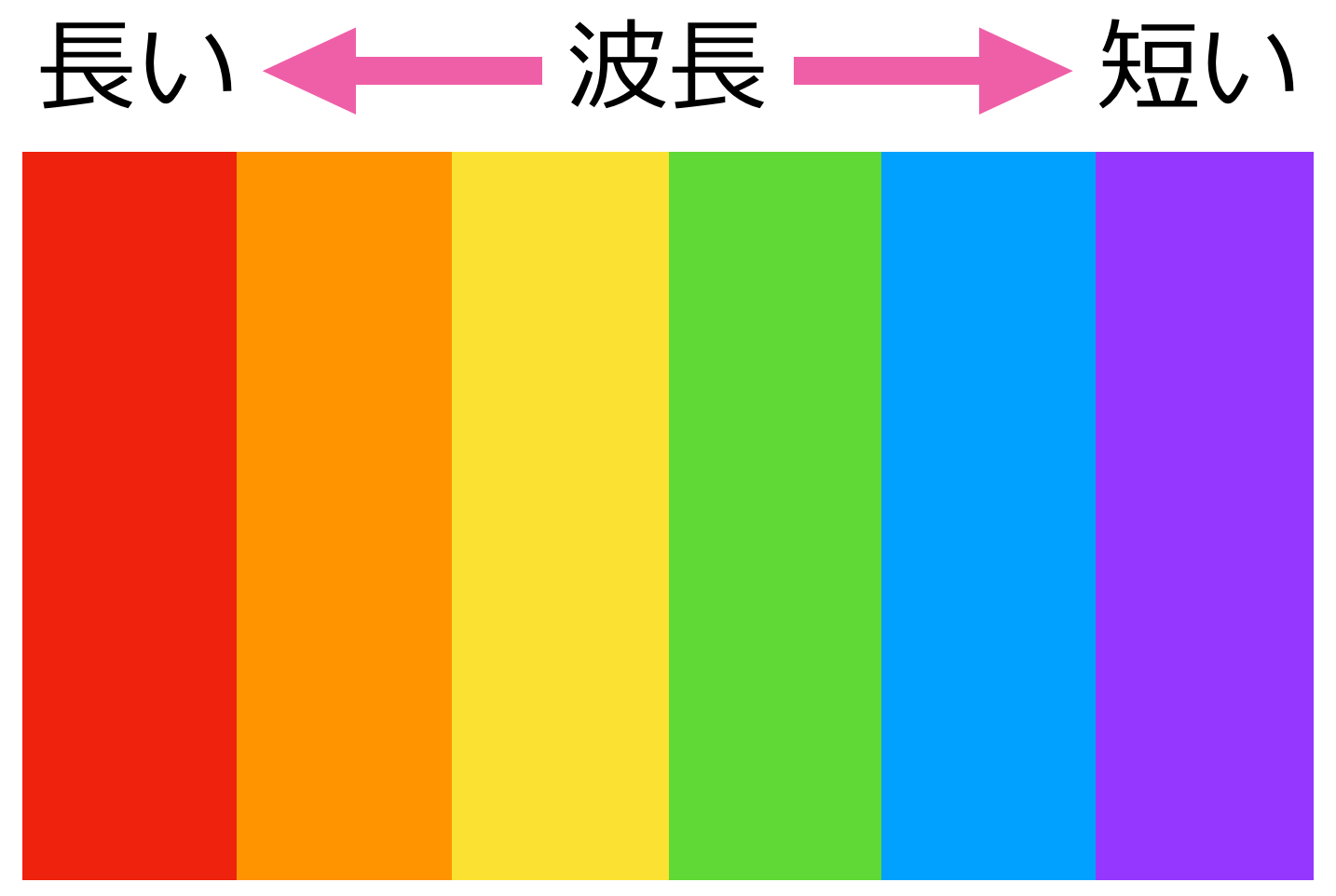
ということは，紫の方が屈折率が大きくなるということよね。
そうだね。そうすると，屈折の時にいっぱい曲がるのは，紫と赤のどっちだろう。
えっと，屈折の法則を考えると，
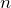
が大きくなると・・・どうなるかな？
数学的に考えると，
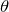
が増加すると90°までは
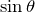
の値も増加するんだよね。だから
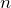
が増加すると，
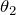
は減少するよね。
基本に戻って考えると，屈折率って，屈折する割合だよね。だから，屈折率が大きい方が大きく屈折するということだよ。
分かりやすい！
ということは，波長の短い紫の方が屈折率が大きいんだから，紫の方がたくさん屈折するっていうことね。問題の図でたくさん屈折すると，Aの方に曲がるので，空欄エの答えは「Ａ」ね。
■媒質中の光の速さ
選択肢を見ると，「速く」か「遅く」だから，波長が違うとプリズム中を進む速さが違うっていうこと？光の速さって一定なんじゃなかったっけ？
光の速さって30万km/sなんだよね。3.0×108m/sね。この値も真空中を光が進むときっていう前提条件があるんだ。媒質中では遅くなるよ。
屈折の法則から分かるんだ。屈折の法則は「屈折」していなくても成り立つので，速さと屈折率の関係のところだけ抜き出してみるよ。
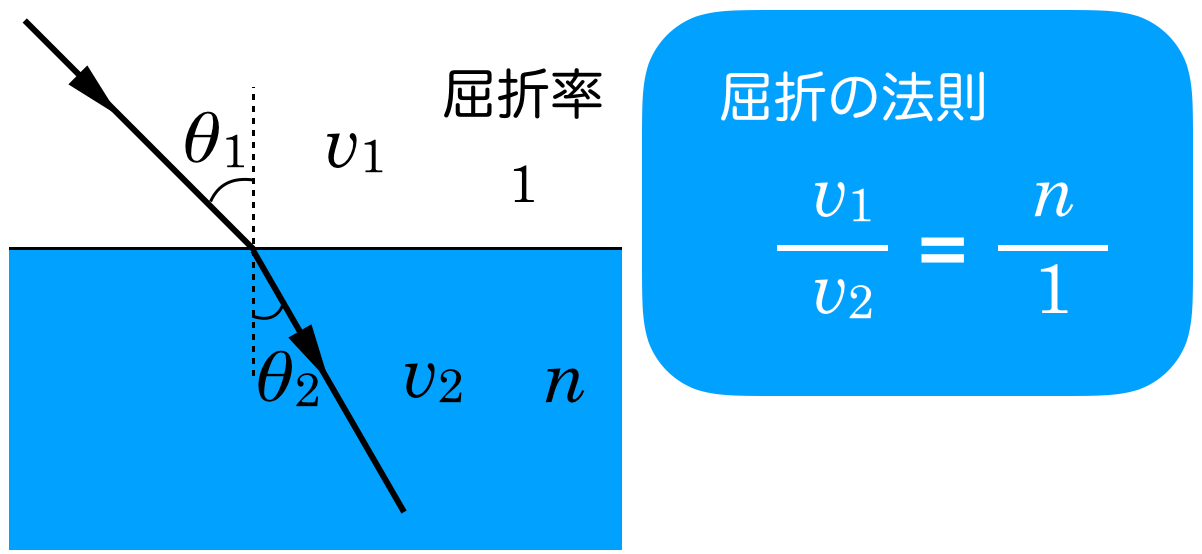
そうなんだよね。この式で，媒質中の光の速さは
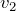
なので，式を変形してみよう。
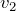
を求めてみればいいのね。
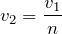
ということは，分母に屈折率が来るから，屈折率が大きい方が遅くなるっていうことね。
問題文の主語は「短い光の方が」となっているので，紫の方が屈折率が大きいので，短い光の方が「遅く」なるということね。
正解だ。空欄には「分散」，「Ａ」，「遅く」の順に入るので，答えは②だね。
