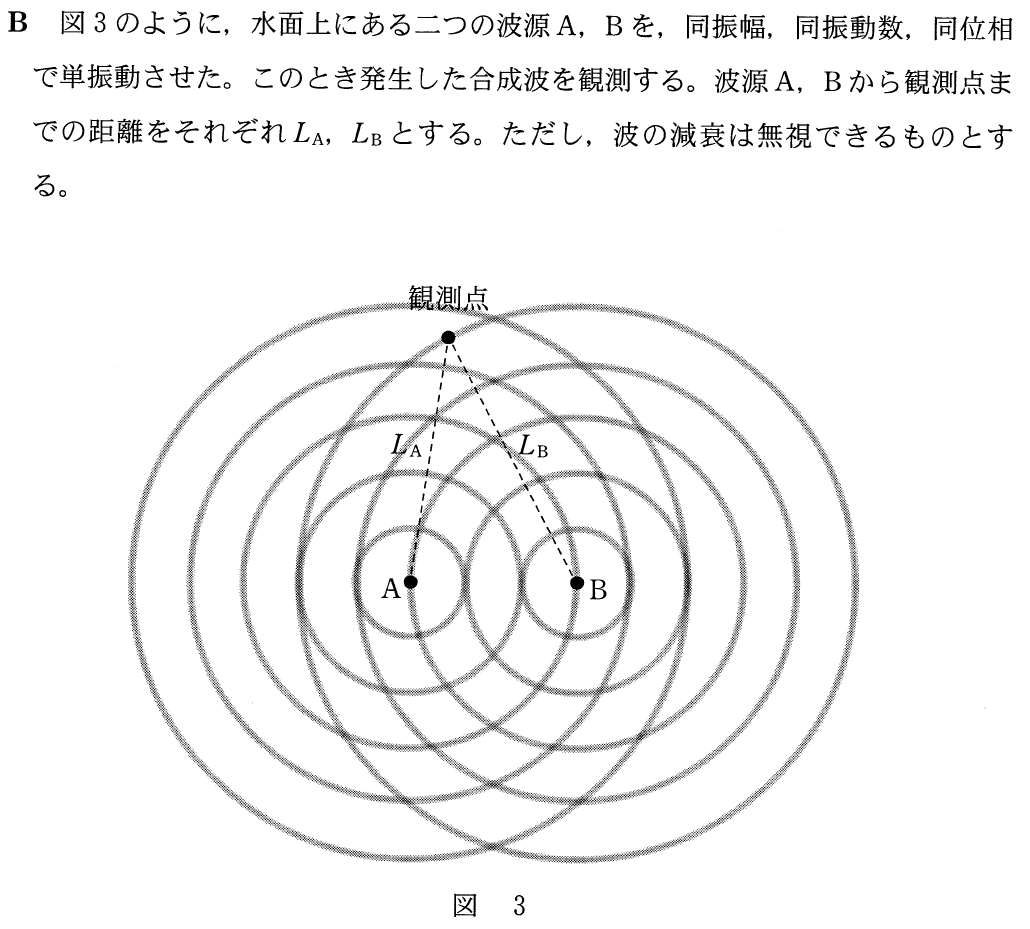

■2つの波の干渉条件
波源Aから出ている波と,波源Bから出ている波を区別するために,ちょっと色分けをしてみようか。
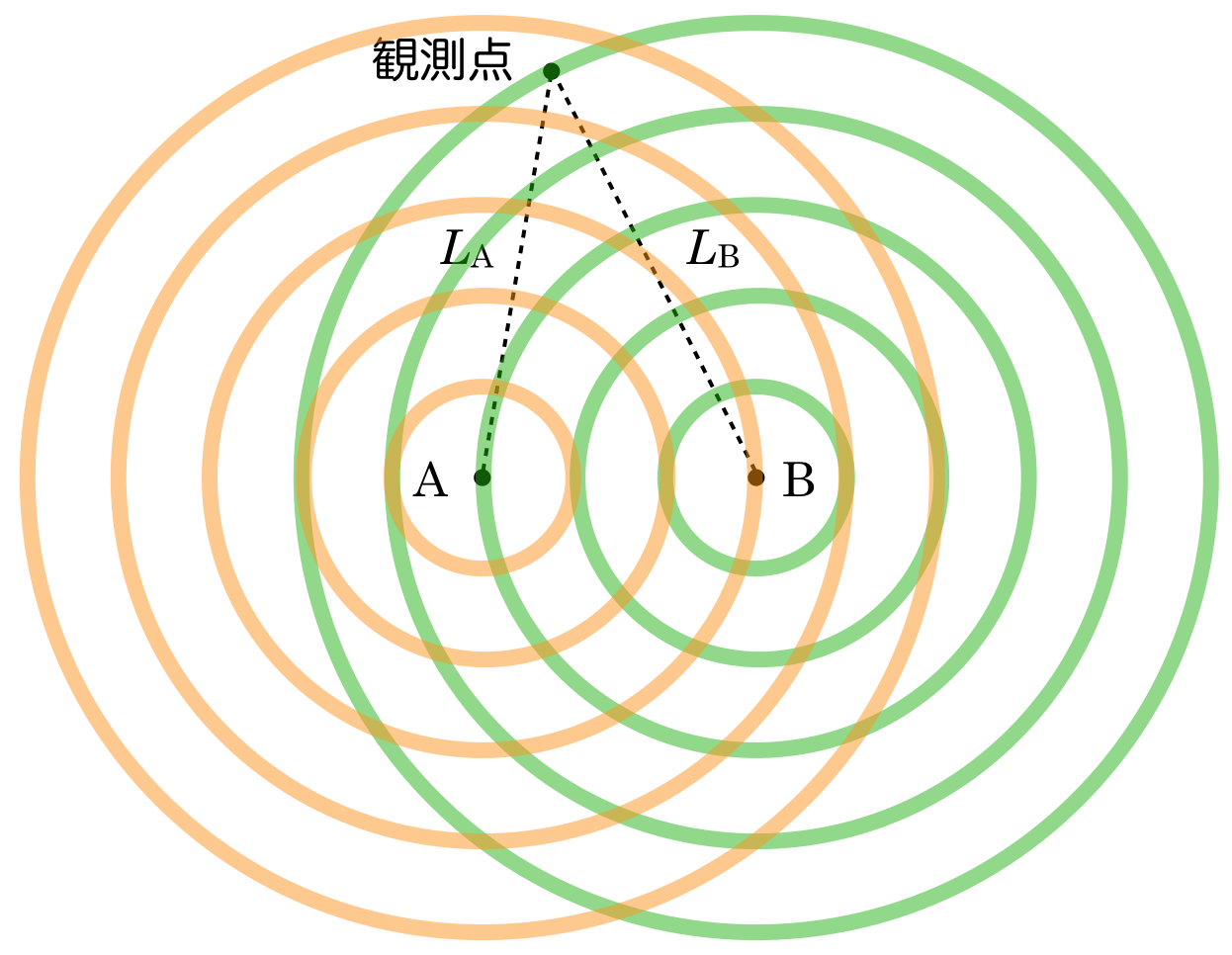
分かりやすくなったわね。この緑とオレンジの線は,”山”と考えていいの?
実はよく分からないんだ。この線が何なのか,問題文のどこにも書かれていないからね。まぁ,山だと考えて問題はないんじゃないかな。
問題はないんだけど,実はこの線はこの問題ではあまり意味がないんだ。だから説明も書かれていないんだね。
「水面波の干渉の話だよ」ということを分かりやすく図にしただけで,無くてもいいんだ。だから取っちゃうよ。
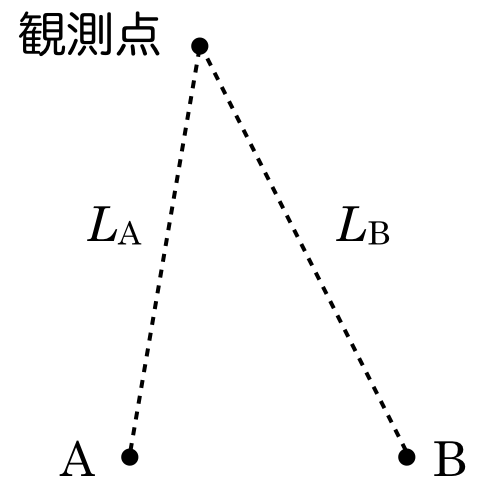
まぁ問題を見てみようか。このA,B2つの波源から発生した波が弱めあう条件を表す式を選べば良いんだね。
2つの波が強め合ったり,弱めあったりすることを「干渉」っていうけど,一般的に干渉して強め合う条件とか,弱めあう条件って覚えていないかな?
「干渉条件」っていうやつね。確かこんな感じよね。ちなみに,
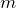
=0,1,2,3‥で,
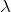
は波長ね。

素晴らしい!そうだね。「経路差」がどんな条件を満たしているか,が大切なんだよね。ちなみに右辺はこんな感じに変形することもあるね。

「半波長の偶数倍」,「半波長の奇数倍」という言葉は聞いたことがあるわ。
変形すればどちらも同じ式だということが分かるね。この問題の選択肢を見ると,今はとりあえず最初の方の関係式で良さそうだね。
■経路差は?
あとは「経路差」を式で表すのね。「経路差」って単純に波源から,観察点までの距離の差よね。
それじゃあ,今は
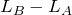
かな?
確かに図では
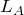
より
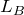
の方が長くなっているけど,問題文を読む限り,観測点の場所は図で指定されている場所とは限らないよね。
そういうこともあるよ。選択肢を見ると経路差が
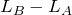
になっているものは無いから,違うって気がつくと思うけどね。
ということは,
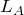
と
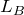
のどちらが長いか分からないということだから,経路差は絶対値を使うのね。

求めたいのは弱めあう条件ね。
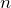
=0,1,2,…だから,こうかな?
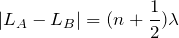
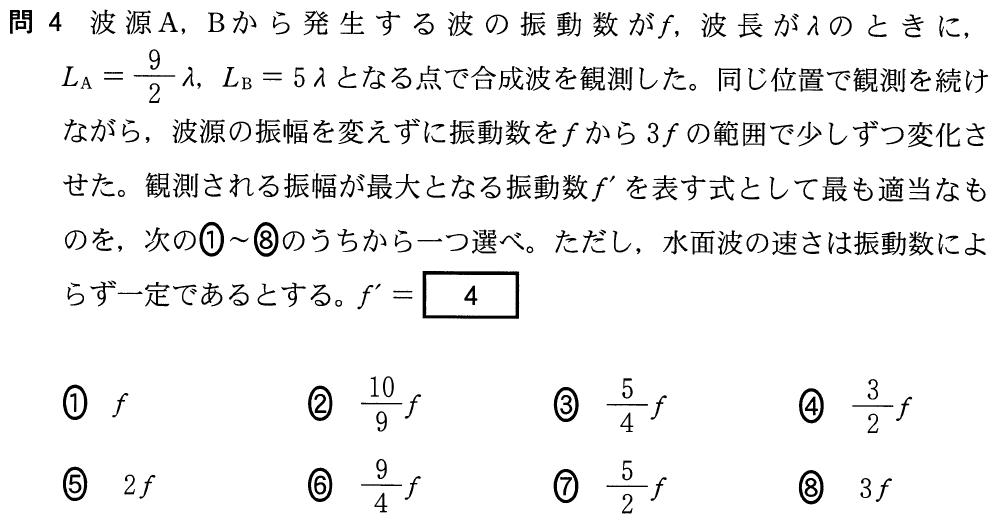
■振動数が変わる
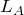
と
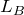
が具体的に与えられたのね。
実はその具体的に与えられた場所が,最初の図の「観測点」なんだよ。
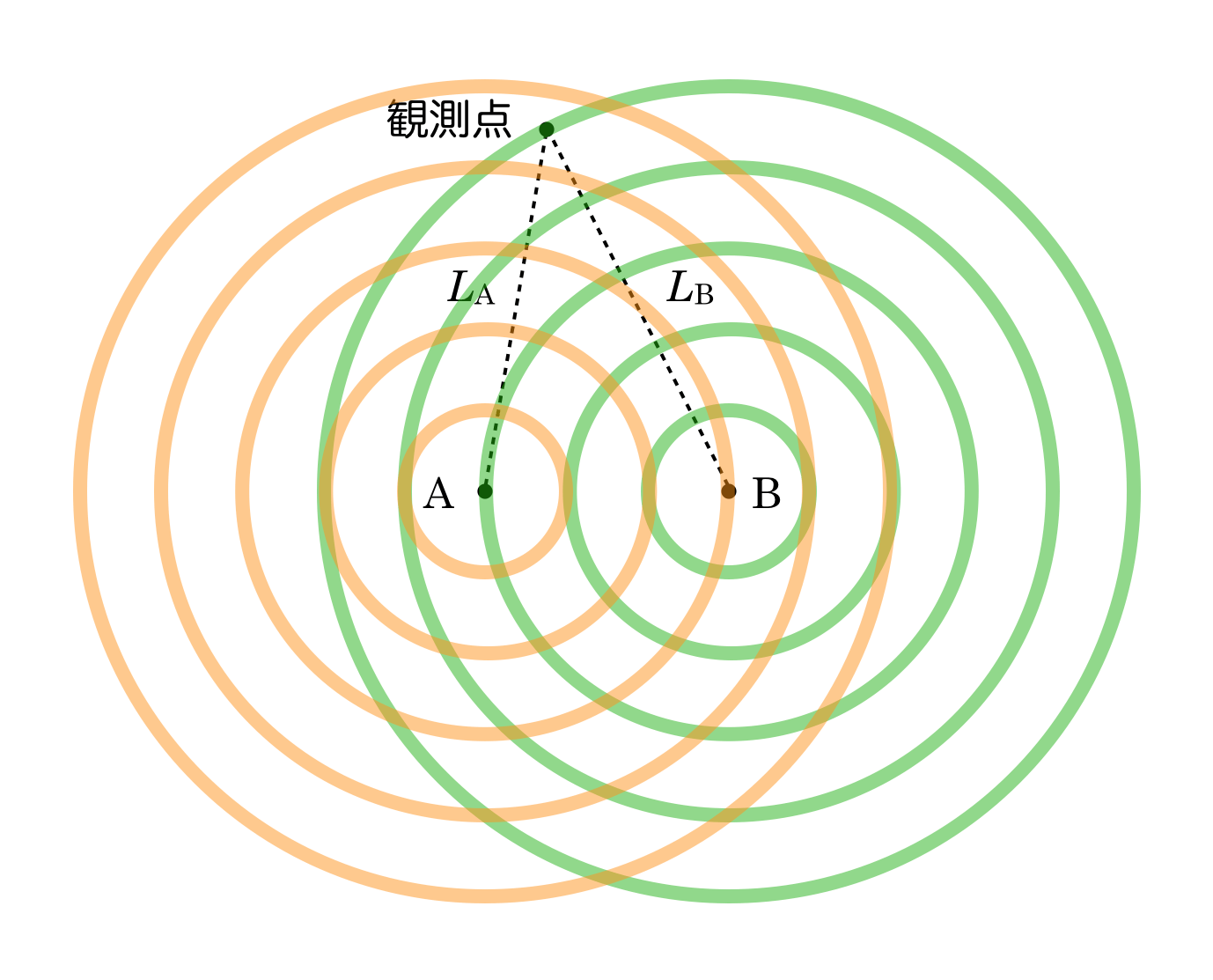
気づかなくても全く問題は無いんだけど,図を使うとイメージしやすいよね。同心円になっている線が山だと考えると,ちょうど
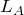
が4.5
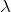
,
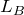
が5
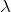
になってるでしょ。
ところで,その観測点は,強め合う点か,弱めあう点か,その他の点か,どうだろう?
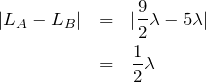
経路差が半波長だから,問3で出した式で,
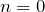
にあたるわね。つまり,弱めあう点ね。
そうだね。現在は弱めあう点なので,振動数を変えるといつかは強め合う点になるはずなんだ。なので,そのときの振動数
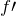
を求めなさいということだね。
振動数を変えても,この同心円の図は変わらないわよね。
確かに図の中に振動数を表す要素はないけど,振動数を変えると,他にも変わる量があるよね。
まず,問題文に「同じ位置で観測を続けながら」とあるので,観測点の場所は変わらないよね。
問題文の最後には「水面波の速さは振動数によらず一定である」とあるから波の速さも変わらないわね。。
ということは,波の分野で良く出てくる式
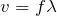
を考えると,波長はどうなるかな?
速さが一定で,振動数が大きくなると,波長は小さくなるわね。
■同心円を描いてみる
そうだね。ちょっと波長を短くした図を描いてみるよ。
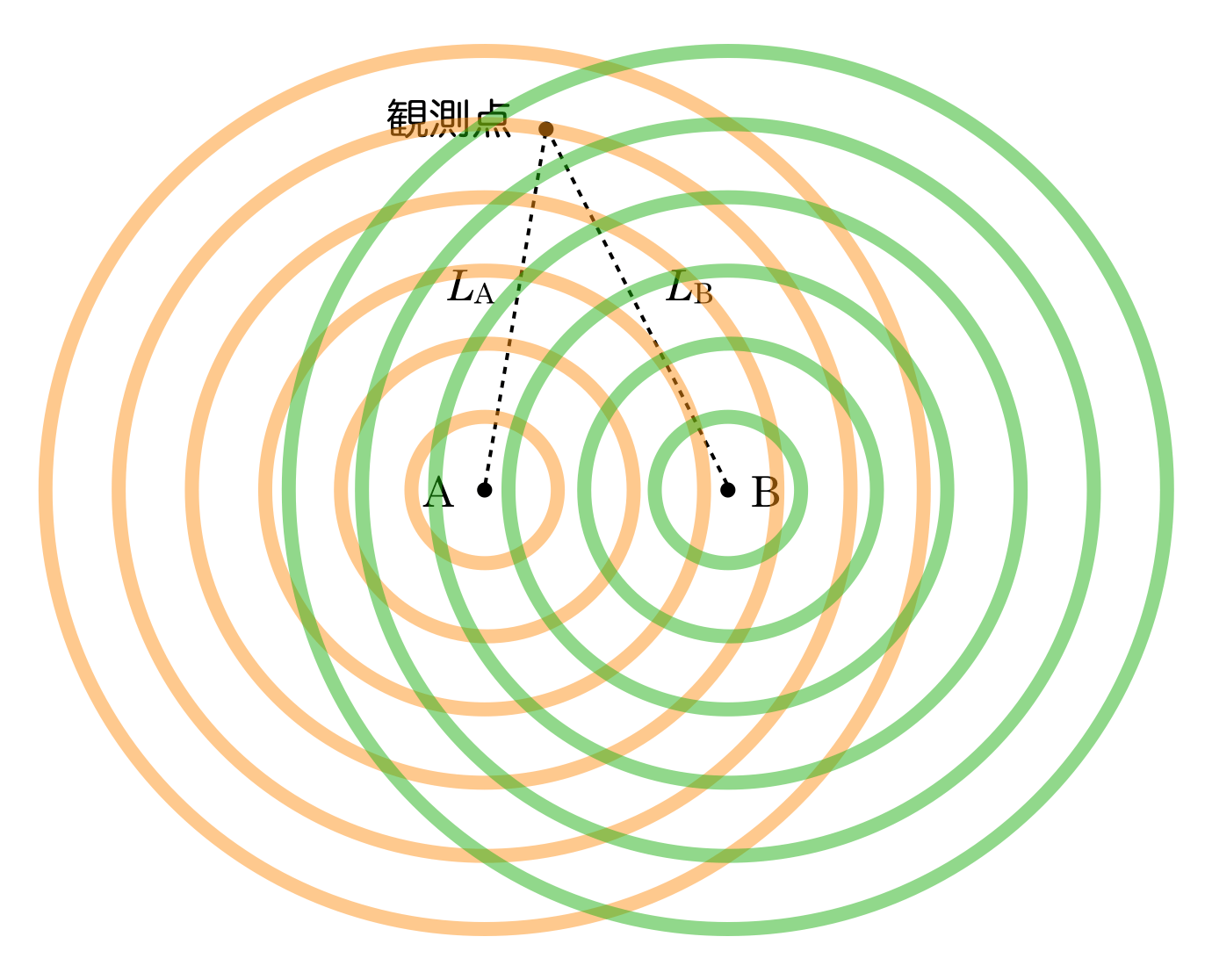
ちょっと分かりにくいけど,どちらの円の半径も少し小さくしたんだ。波長が短くなるということは,山と山の間隔が短くなるということだからね。もちろん,観測点の位置は動かしてないよ。
波長が短くなると,円の半径が小さくなるのは分かるわ。ただ,前の図との違いは分かりにくいわね。
最初の図では観測点は緑色の円の上にあったけど,この図ではオレンジ色の円の上にあるよね。
なるほど。観測点がどうなっているかに注目すれば良いのね。確かに2つの図を並べて比較すると,最初の左の図よりも,右の図の方が円の間隔が狭いわね。
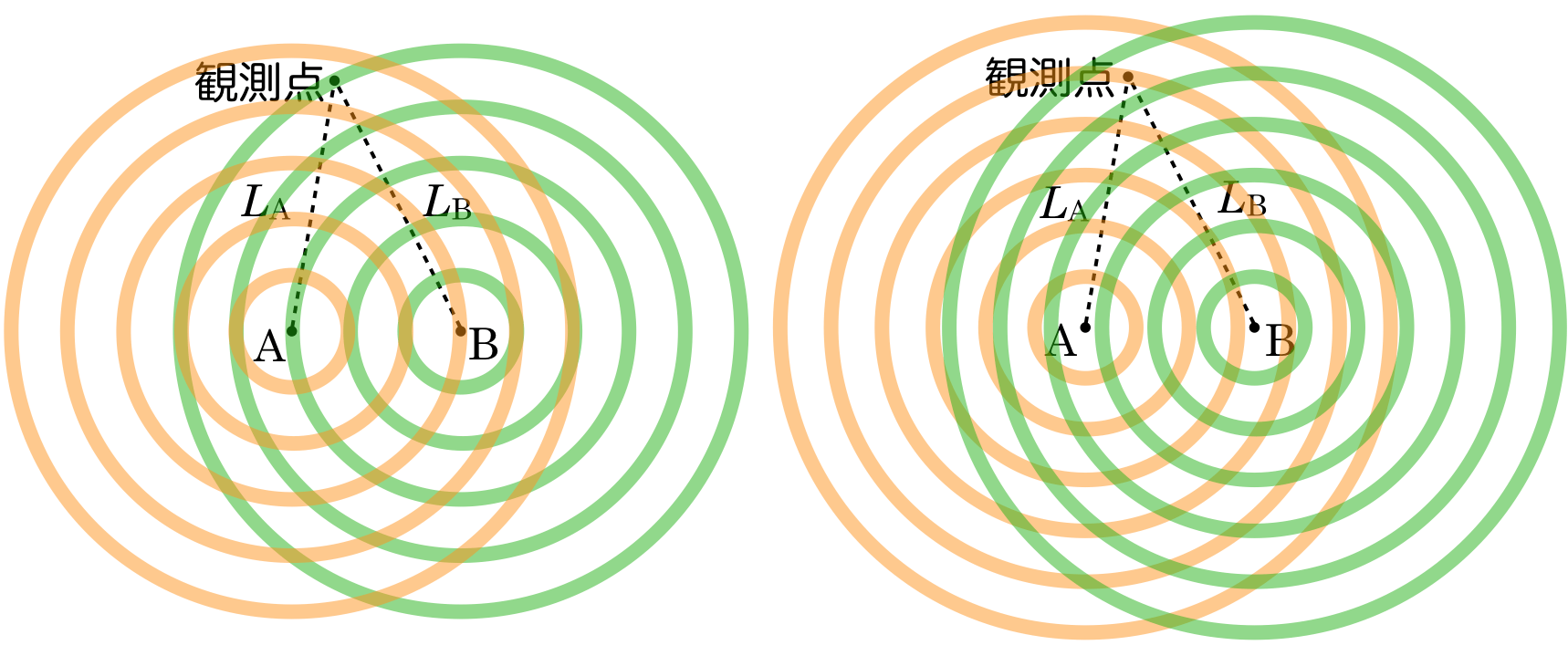
そうでしょ。ただ,観測点で強め合うためには山と山が重なるか,谷と谷が重なっている必要があるんだ。まだ重なっていないので,もう少し円の半径を小さくしてみようか。
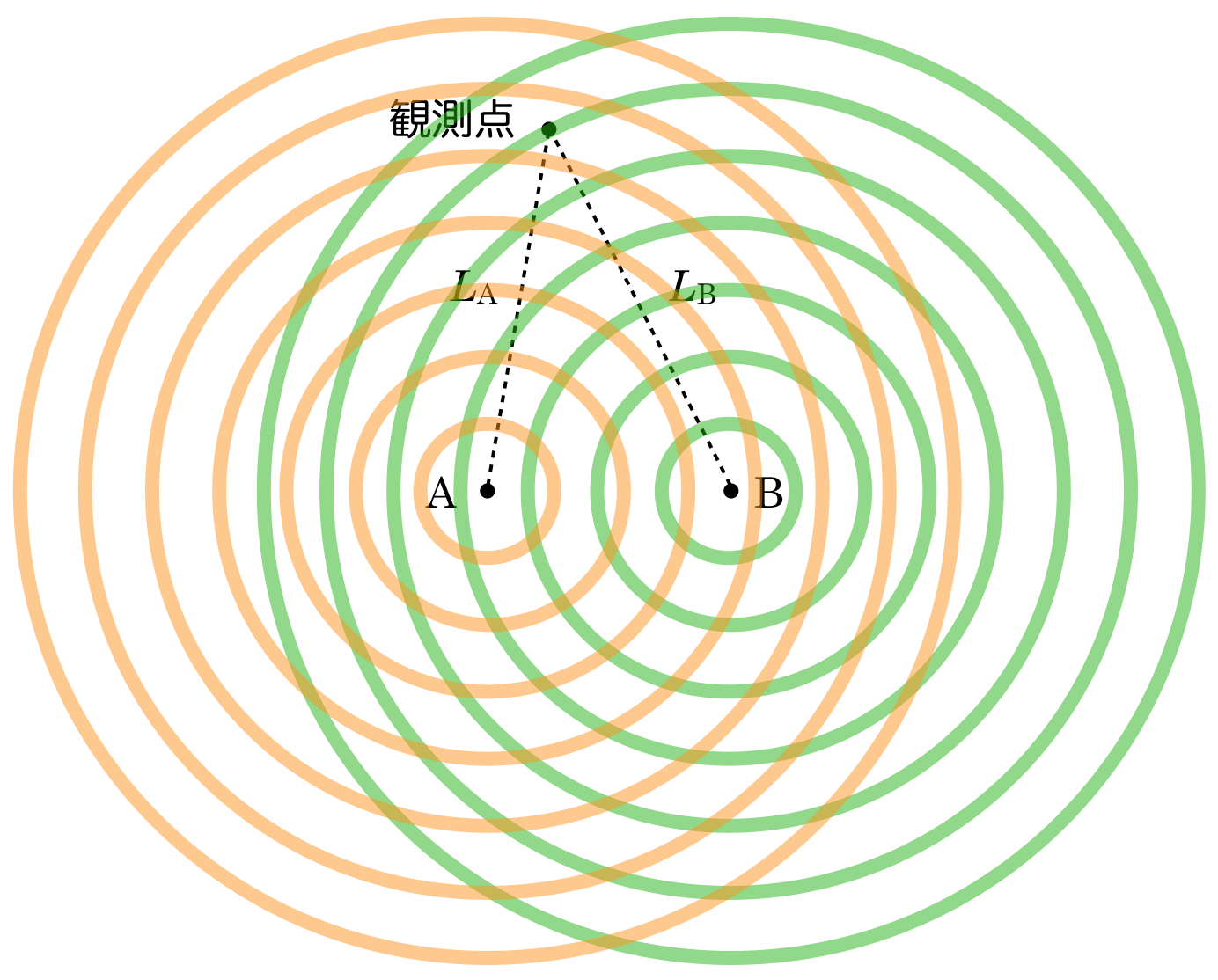
なかなか観測点で山と山,谷と谷が重なる感じにはならないわね。
■経路差を図で考えてみる
そうだね。ちょっと戻って考えてみようか。まずこの長さを経路差としようか。

最初,波の振動数が
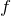
,波長が
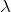
のとき,経路差は半波長だったんだよね。
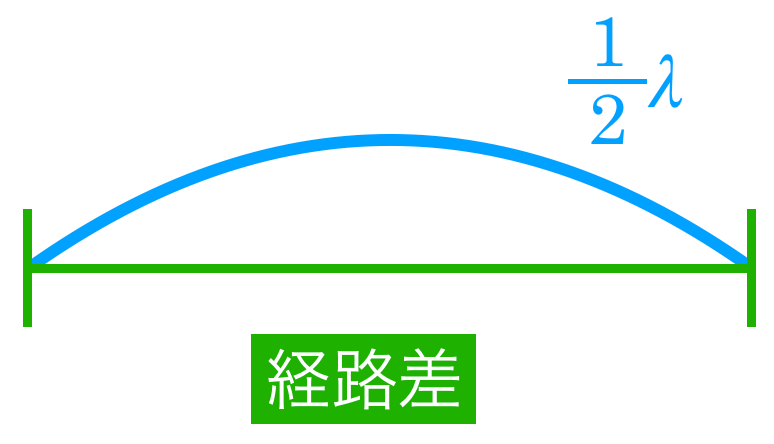
波長が短くなって
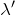
になったとき,経路差がどうなれば強め合う点になるかな?
強め合うためには,「経路差=
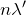
」であればいいのよね。今の場合は経路差が0になることはないから,次に強め合うのは
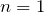
ね。

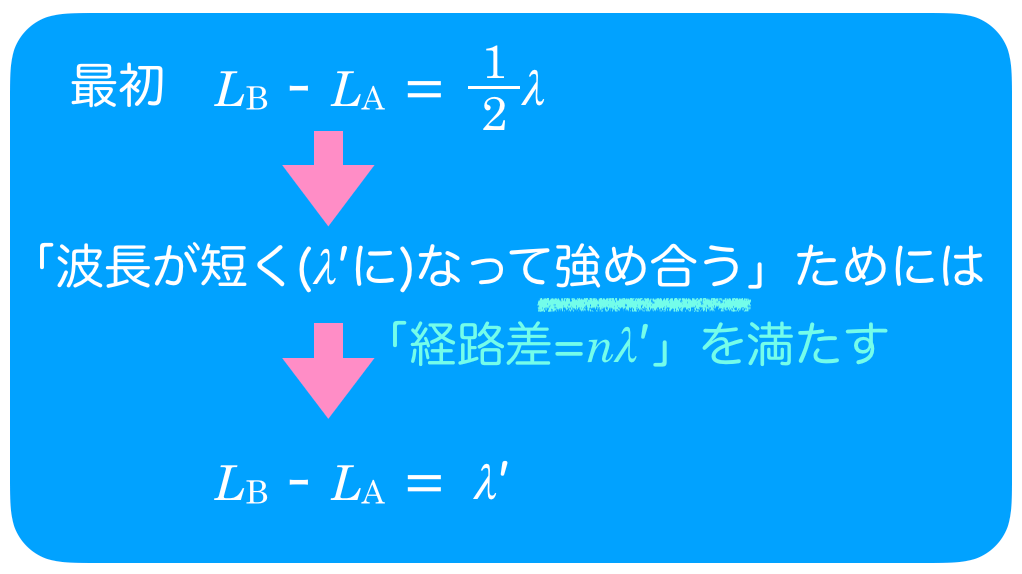
経路差である
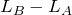
は変わらないから,まとめに書いた2つの式を合わせると,こうなるよね。
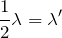
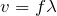
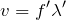
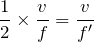
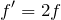
それが答えだね。⑤が答えだ。ちなみに,振動数が2倍になるということは,波長が半分になるということで,観測点が強め合うときの同心円の図を描いてみると,こんな感じになるよ。
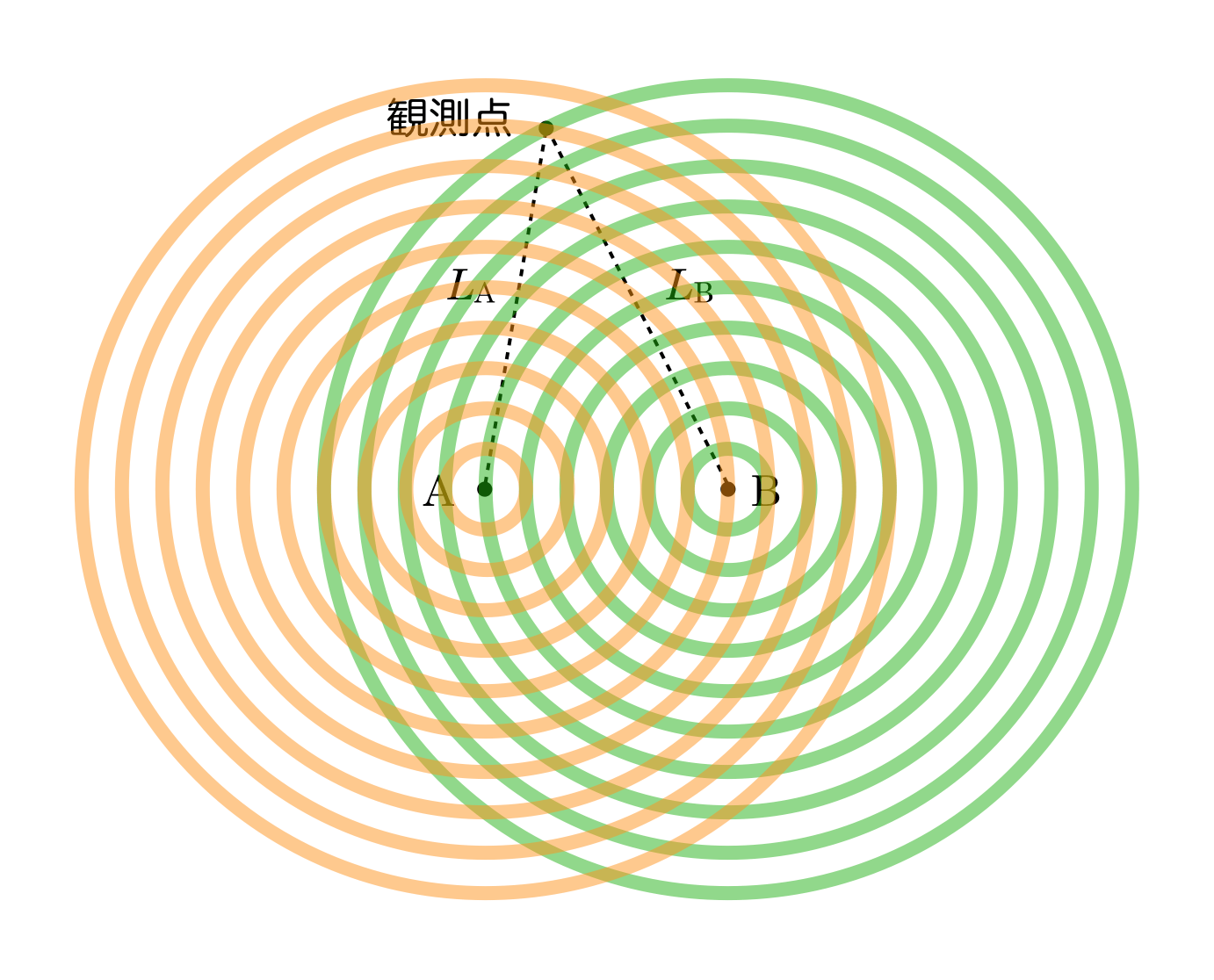
円と円の間隔がかなり狭くなったけど,確かに観測点でどちらの波も山になっているわね。




![]() =0,1,2,3‥で,
=0,1,2,3‥で,![]() は波長ね。
は波長ね。

![]() かな?
かな?![]() より
より![]() の方が長くなっているけど,問題文を読む限り,観測点の場所は図で指定されている場所とは限らないよね。
の方が長くなっているけど,問題文を読む限り,観測点の場所は図で指定されている場所とは限らないよね。![]() になっているものは無いから,違うって気がつくと思うけどね。
になっているものは無いから,違うって気がつくと思うけどね。![]() と
と![]() のどちらが長いか分からないということだから,経路差は絶対値を使うのね。
のどちらが長いか分からないということだから,経路差は絶対値を使うのね。
![]() =0,1,2,…だから,こうかな?
=0,1,2,…だから,こうかな?![]()

![]() と
と![]() が具体的に与えられたのね。
が具体的に与えられたのね。
![]() が4.5
が4.5![]() ,
,![]() が5
が5![]() になってるでしょ。
になってるでしょ。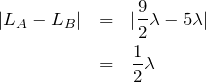
![]() を求めなさいということだね。
を求めなさいということだね。![]() を考えると,波長はどうなるかな?
を考えると,波長はどうなるかな?



![]() ,波長が
,波長が![]() のとき,経路差は半波長だったんだよね。
のとき,経路差は半波長だったんだよね。
![]() になったとき,経路差がどうなれば強め合う点になるかな?
になったとき,経路差がどうなれば強め合う点になるかな?![]() 」であればいいのよね。今の場合は経路差が0になることはないから,次に強め合うのは
」であればいいのよね。今の場合は経路差が0になることはないから,次に強め合うのは![]() ね。
ね。

![]() は変わらないから,まとめに書いた2つの式を合わせると,こうなるよね。
は変わらないから,まとめに書いた2つの式を合わせると,こうなるよね。![]()
![]()
![]()
![]()
![]()