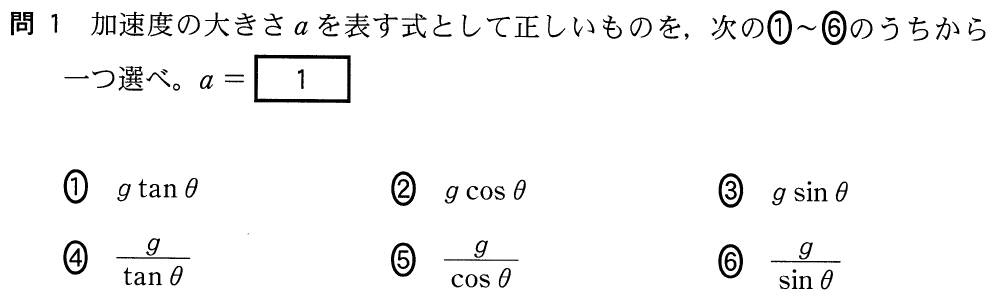
■とりあえず力の矢印を描く
物理が苦手な文子
電車の加速度を求める問題ね。等加速度直線運動の式は使えなさそうね。使えそうな情報が少ないから。
物理が得意な秀樹
そうだね。他に加速度を求める方法はあるかな?
物理が苦手な文子
運動方程式かな?ただ,電車にはたらいている力が分からないから,使えないか。
物理が得意な秀樹
実際は小物体に対して運動方程式を立てると,答えが出るね。それでもいいんだけど,電車の中に観測者がいるので,観測者の視点で考えてみない?
物理が苦手な文子
観測者の視点で運動方程式を立てるの?
物理が得意な秀樹
いやいや違うよ。問題文に「電車に乗っている観測者から見て,(中略)静止した。」ってあるよね。
物理が苦手な文子
静止したっていうことは,力のつり合いの式を立てるの?
物理が得意な秀樹
その通り。
物理が苦手な文子
でも,力のつり合いの式だと,加速度が出てこないんじゃない?
物理が得意な秀樹
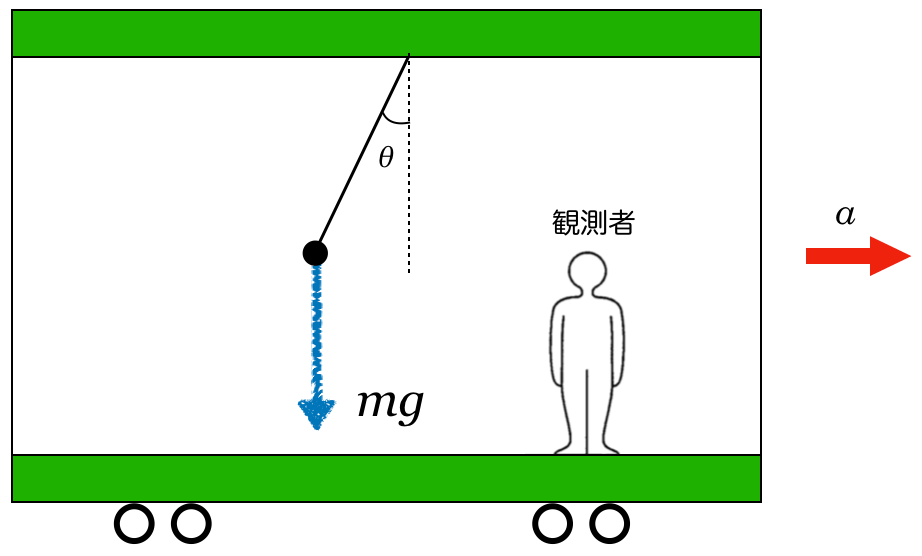
観測者が加速しているので,力のつり合いの式だけど,加速度が含まれるんだ。ちょっとやってみよう。小物体にはたらく力の矢印を描くとどうなるかな?力の矢印の描き方はこんな感じだよね。

物理が苦手な文子
まずは,重力を描くのね。重力は鉛直下向きで,大きさは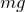 でいいわよね。
でいいわよね。
物理が苦手な文子
くっついているものは糸しかないので,糸から受ける力を描くわね。糸の向きに大きさはとりあえず としておくわね。
としておくわね。
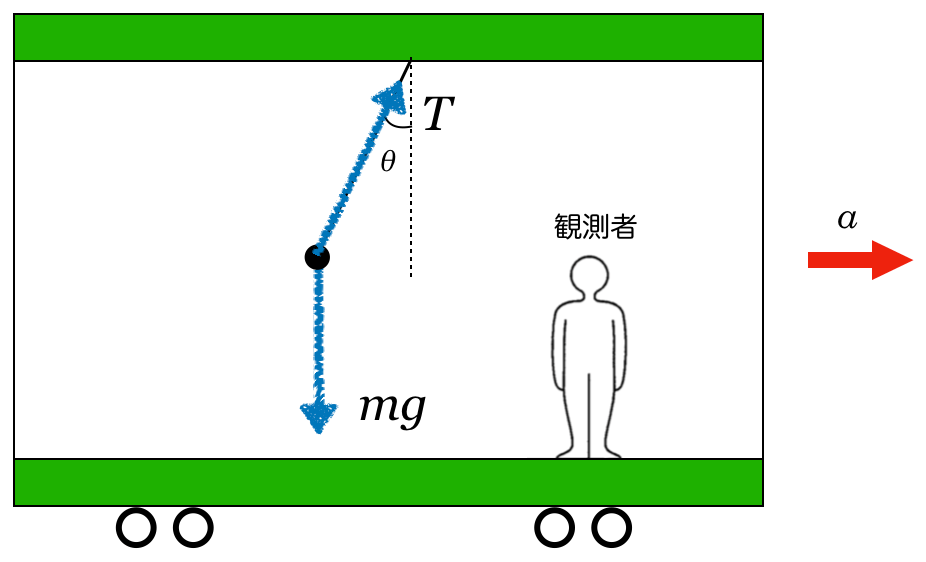
物理が得意な秀樹
いいね。あとは?
物理が苦手な文子
あとくっついているものは無いので,これで終わりね。
物理が得意な秀樹
そうだね。ただ,この2つの力だけだと,力はつり合わないよね。つり合わない場合は,運動方程式を立てる方法もあるんだけど,今は電車の中の観測者から見て,力のつり合いの式を立てるよ。
■慣性力を考える
物理が苦手な文子
電車の中の観測者から見ると,どうなるの?
物理が得意な秀樹
電車の中の観測者は,電車と一緒に加速してるんだよね。観測者が加速しているときに考える見かけの力があるんだけど,覚えてる?
物理が苦手な文子
確か「慣性力」ね。加速している人から見ると,加速度と逆向きに大きさ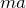 の力がはたらいているように見えて,その力を「慣性力」というのよね。
の力がはたらいているように見えて,その力を「慣性力」というのよね。

物理が得意な秀樹
その通り!じゃあ,慣性力を図に描いてみるとどうなるかな?
物理が苦手な文子
電車は右向きに加速しているから,慣性力は左向きね。
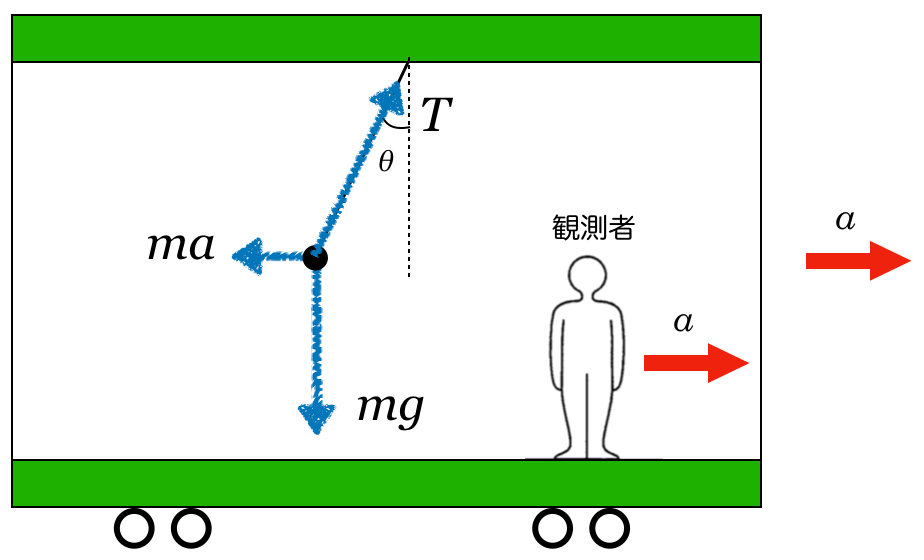
物理が得意な秀樹
電車の中にいる観測者から見ると,この3つの力がはたらいていて,小物体は静止して見えるんだ。
■力のつり合いの式を立てる
物理が苦手な文子
あとは観測者から見た力のつり合いの式を立てれば良いのね。
物理が得意な秀樹
この問いの答えを出すだけだったらもう少し簡単な方法もあるけど,力のつり合いの式を立てるやり方は,どんな場合も使えるので,やっぱり力のつり合いの式を立てよう。
物理が苦手な文子
水平方向を 軸,鉛直方向を
軸,鉛直方向を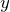 軸とするわね。まず,糸の張力
軸とするわね。まず,糸の張力 を分けなきゃダメね。
を分けなきゃダメね。
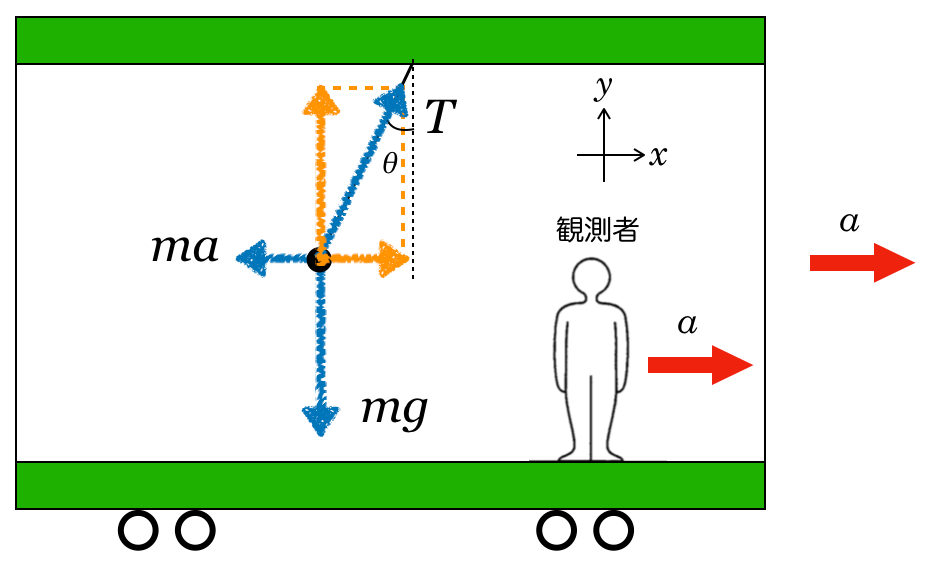
物理が得意な秀樹
そうすると,分けた力の大きさはどうなるかな?
物理が苦手な文子
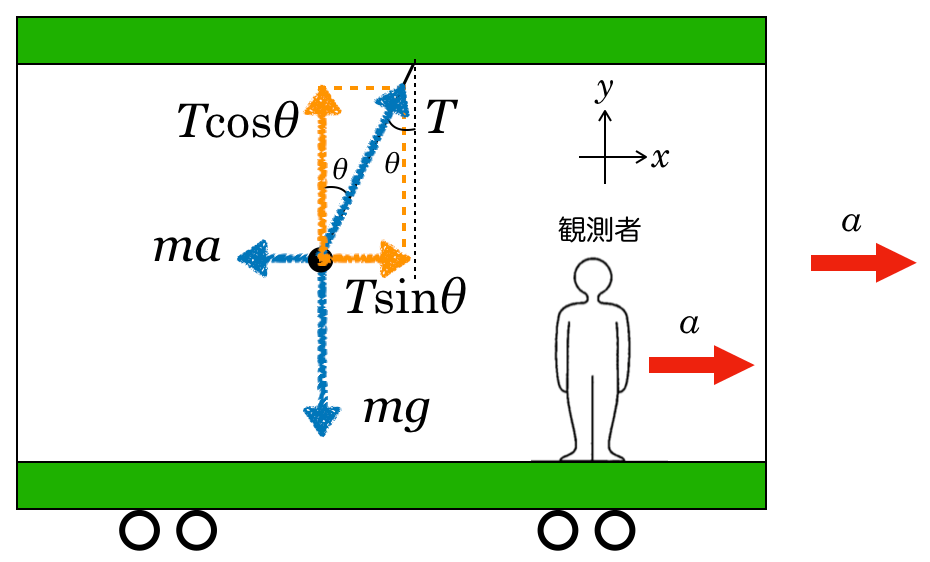
物理が得意な秀樹
いいぞ,力のつり合いの式を立ててみよう。
物理が苦手な文子
計算してみるわ。
![]()
![]()
![]() 方向
方向
![]()
![]()
①÷②
![]()
![]()
![]()
物理が得意な秀樹
正解だ。答えは①だね。次は問2。
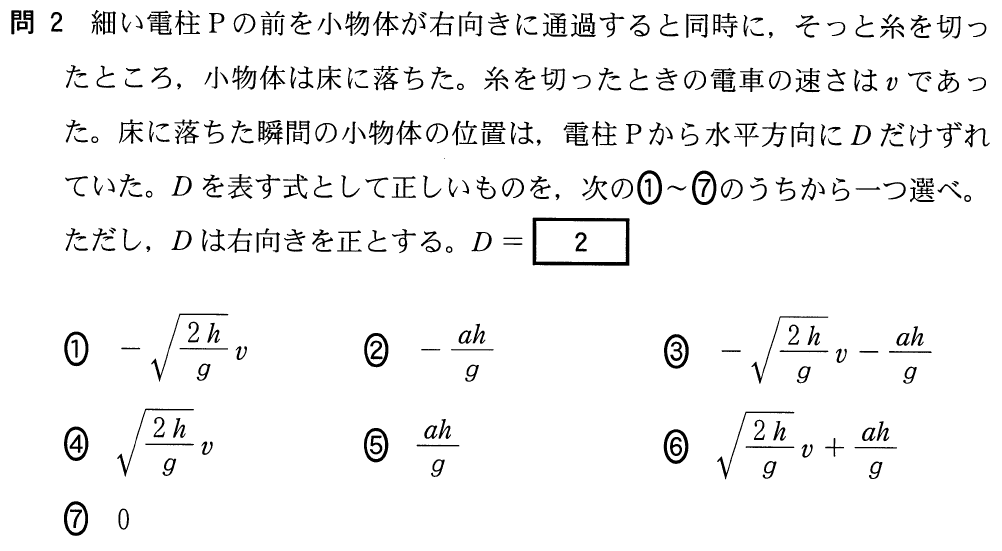
■今度は静止している観測者を考える
物理が得意な秀樹
電車は加速していて,
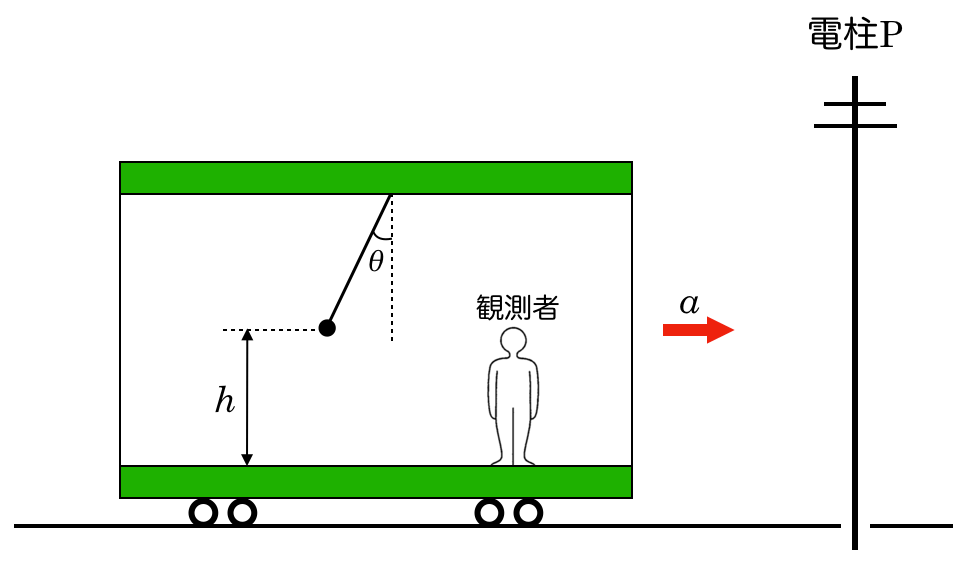
物理が得意な秀樹
電柱Pと小物体が重なった瞬間,糸を切ったということだよね。
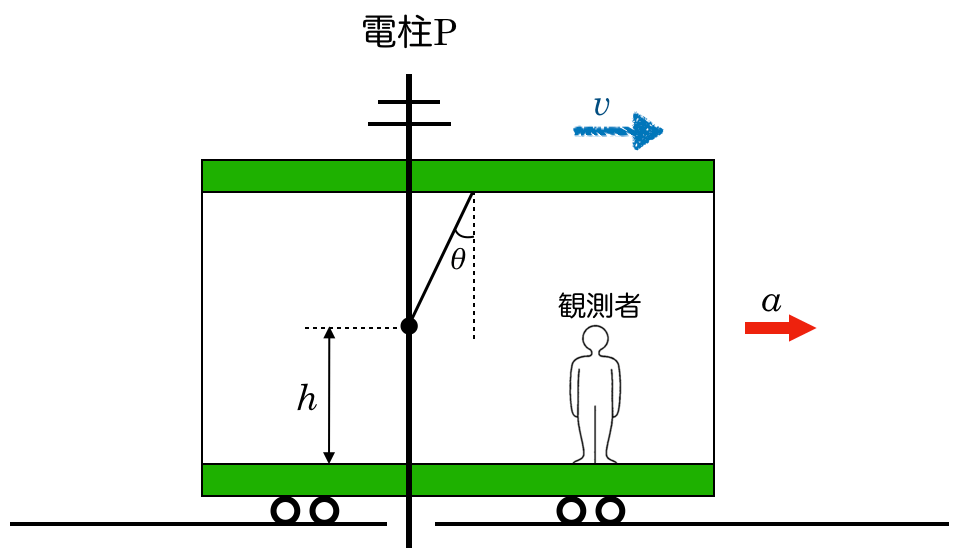
物理が得意な秀樹
さて,糸を切った後,小物体はどう動くかな?
物理が苦手な文子
それって,電車の中の人が見るの?電車の外の人が見るの?
物理が得意な秀樹
確かに観測者によって,小物体の運動は変わるね。この問いでは電車の中と外,どっちの立場が良いと思う?
物理が苦手な文子
電車の床に落ちるから,電車の中の人かな?
物理が得意な秀樹
でも求めたいのは電柱Pからのずれだよ。
物理が苦手な文子
電柱は電車の外で静止しているのね。じゃあ,電車の外に観測者がいるとして,考えた方が良いの?
物理が得意な秀樹
この場合はそうだね。電車の中の観測者から見ると,小物体にも電柱Pにも慣性力がはたらいているとして,考えなければならないので,たいへんでしょ。
物理が苦手な文子
なるほど。
物理が得意な秀樹
それじゃあ,電車の外で静止している人から見ると,糸を切った後の小物体の動きは,どうなるでしょう?
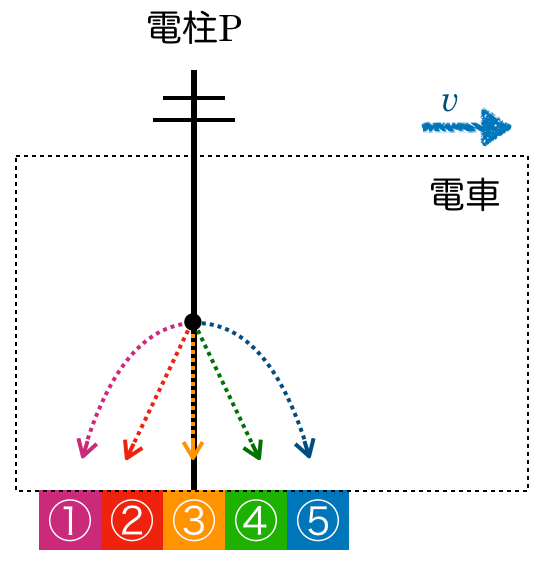
物理が苦手な文子
電車は右向きに加速しているので,電車の後ろの方に行きそうな気がする。つまり①か②かな。
物理が得意な秀樹
確かに電車から見ると,後ろの方に行きそうだけど,今は外で静止している人が見るんだよ。
物理が苦手な文子
でも,電車の前に行くことはないんじゃない?
■小物体にはたらく力と初速度を考える
物理が得意な秀樹
糸が切れたら,小物体にはたらく力はどうなるの?
物理が苦手な文子
重力と,えっと,外の人が見るから慣性力は考えなくて良いので,重力だけ?

物理が得意な秀樹
そうだね。重力だけだ。だとすると,どんな運動をする?
物理が苦手な文子
自由落下運動かな?だとすると,真下に落ちるの?
物理が得意な秀樹
重力だけを受けて運動するのは,自由落下運動だけとは限らないね。自由落下運動は「初速度が0」っていう条件があるからね。
物理が苦手な文子
糸が切れたときの,鉛直方向の速度は0でしょ?
物理が得意な秀樹
確かに鉛直方向の速度は0だね。でも水平方向の速度はあるよね。

物理が苦手な文子
あっそうか,はたらいている力は重力だけでも,水平方向の初速度を持っていれば,水平投射になるのね。水平投射ということは,放物運動?
物理が得意な秀樹
電車の外で静止している人から見ると,小物体は放物運動するんだ。
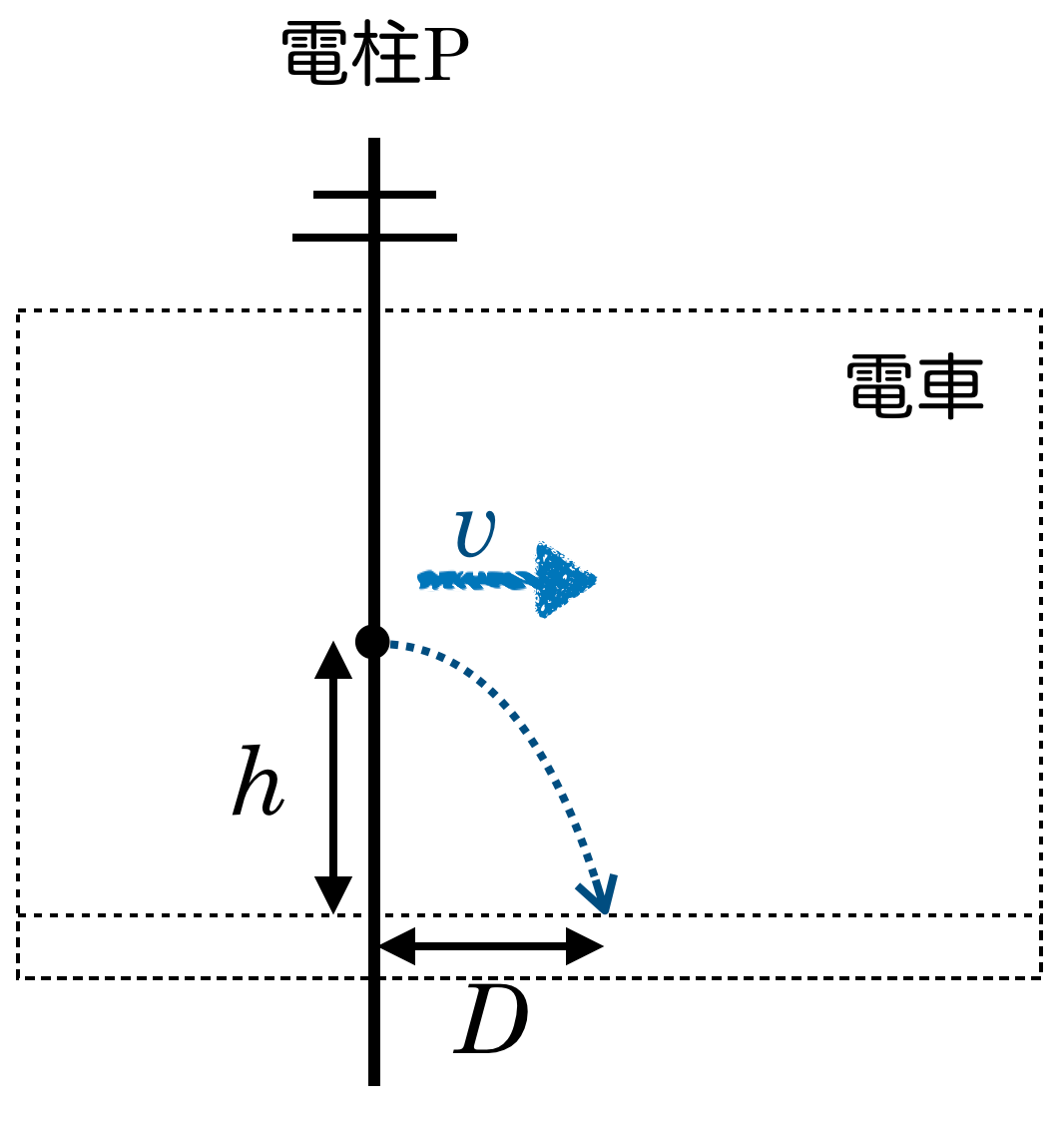
物理が苦手な文子
床に落ちた位置と電柱の距離を求めるのね。電柱の右に落ちることは確実のなので,選択肢の④〜⑥のどれかね。
物理が得意な秀樹
そうだね。
物理が苦手な文子
これってどうやって求めるんだっけ?
物理が得意な秀樹
公式に代入すれば求まる,という感じではないね。求めたいのは水平方向の長さなんだけど,水平方向だけ考えると,どういう運動かな?
物理が苦手な文子
水平方向に力ははたらいていないから,等速直線運動ね。速さは ね。
ね。
物理が得意な秀樹
そうだね。じゃあ鉛直方向は?
物理が苦手な文子
鉛直方向は初速度0で重力だけを受ける自由落下運動よね。
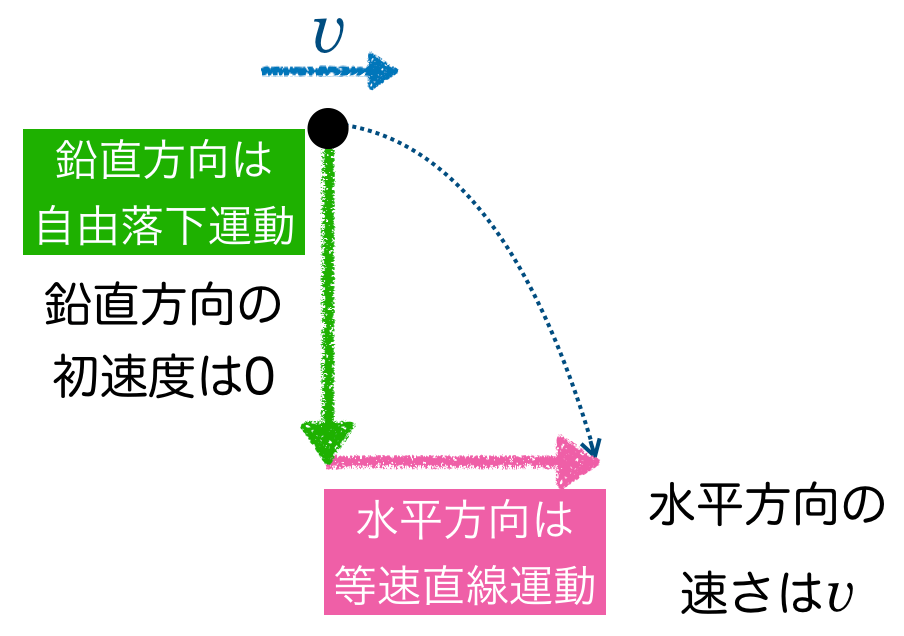
物理が得意な秀樹
水平方向の移動距離は,時間が分かれば求まるよね。なので,鉛直方向の運動から時間を求めたいね。
物理が苦手な文子
ということは,
等加速度直線運動の式
![]()
を使うと,
![]()
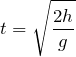
物理が得意な秀樹
時間が出たね。あとは水平方向は等速運動だよね。
物理が苦手な文子
単純に「距離=速さ×時間」でいいわね。
![]()
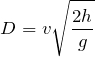
物理が得意な秀樹
その通り!答えは④だ。最後に問3だ。

■再び電車内の観測者を考える
物理が苦手な文子
今度は電車の中の観測者が見たときの小物体の運動ね。
物理が得意な秀樹
それじゃあ,観測者から見ると小物体はどう動くか分かるかな?
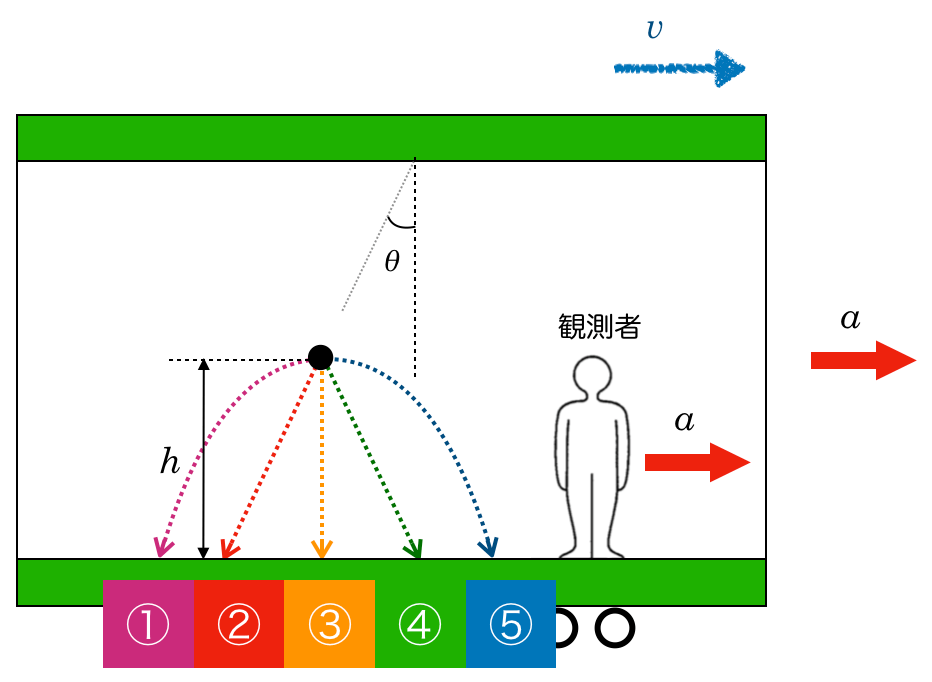
物理が苦手な文子
やっぱり電車の中から見ると,後ろに行くわよね。だからやっぱり,①か②じゃやないかな。
物理が得意な秀樹
ある程度予想を立てるのは大切だよね。次に問2と同じで,力の矢印を考えて,さらに初速度の向きを考慮することも大切だったよね。
物理が苦手な文子
それじゃあまず力の矢印を描くけど,糸が切れた後の話だから問2と同じで,重力だけよね。
物理が得意な秀樹
問2とのの違いは,観測者が加速しているので,慣性力を考えなきゃダメということだね。
物理が苦手な文子
あっそうか,こういうことね。
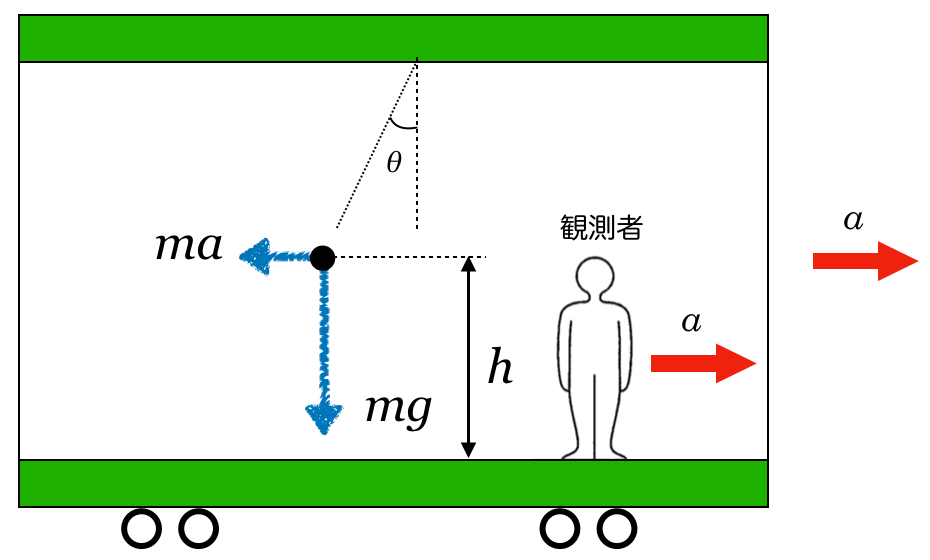
物理が得意な秀樹
そうだね。
物理が苦手な文子
今度は水平方向にも力がはたらいているから,また水平方向と鉛直方向に分けて考えれば良いわね。
物理が得意な秀樹
それでもいいんだけど,水平方向も鉛直方向も加速度を考えなきゃダメなので,どんな運動になるか分かりにくいでしょ。
■合力を考える
物理が苦手な文子
ということは,分けずに考えるっていうこと?
物理が得意な秀樹
そう,逆に合力を考えるんだ。こんな感じだよ。
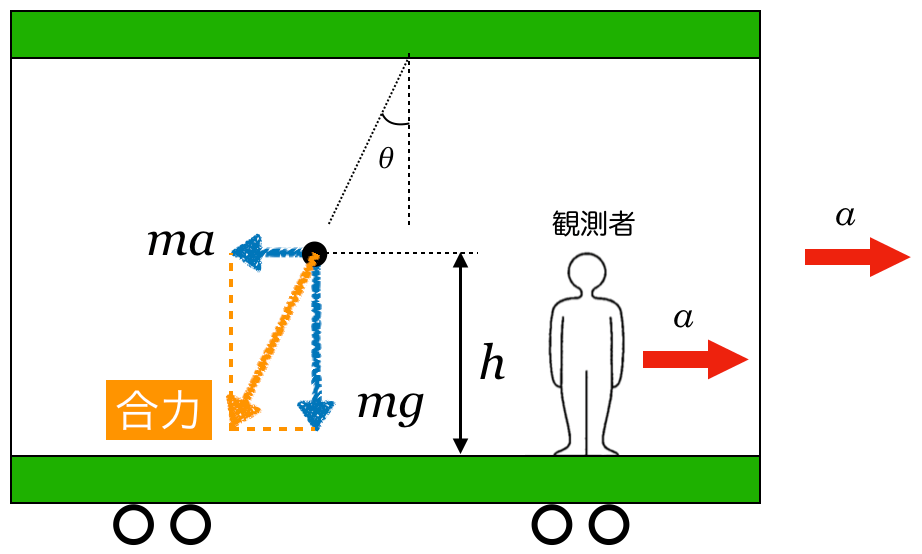
物理が苦手な文子
合力は分かるんだけど,このあとはどうするの?
物理が得意な秀樹
この合力の向きは分かるかな?
物理が苦手な文子
合力の向き?分かるの?
物理が得意な秀樹
糸が付いているときは,重力,糸の張力,慣性力で力がつり合っていたんだよね。ということは,重力と慣性力の行力は,糸の張力と逆向きでしょ。
物理が苦手な文子
そういうことか,糸が切れても重力と,慣性力は変わらないもんね。ということはここが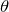 ね。
ね。
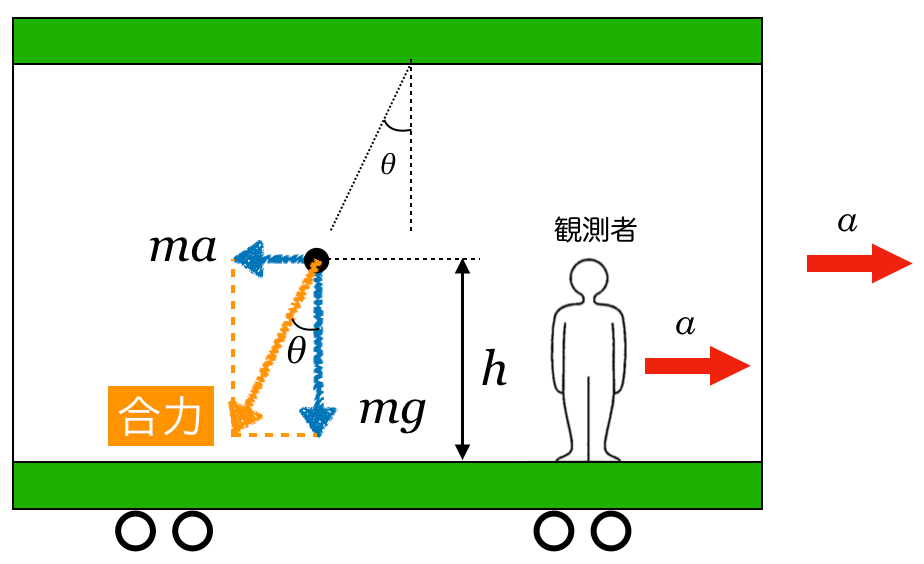
物理が得意な秀樹
さて,糸が切れた直後の初速度はどうかな?
物理が苦手な文子
もともと観測者から見て静止していたんだから,初速度は0ね。
物理が得意な秀樹
その通り。それじゃあ小物体はどう動くかな?
物理が苦手な文子
合力の方向に動くの?
物理が得意な秀樹
そうだね。合力の方向に加速していくんだね。
物理が苦手な文子
合力の向きは動き出しても変わらないわよね。
物理が得意な秀樹
そうだね。だから,合力の向きに等加速度直線運動をするんだね。
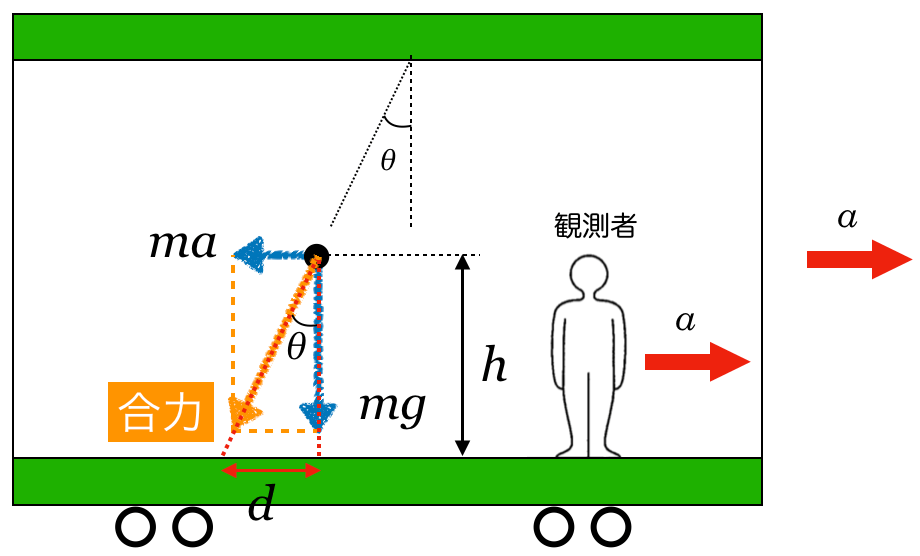
物理が苦手な文子
ということは等加速度直線運動の式で求めるの?
物理が得意な秀樹
求めたいのは水平方向の長さ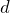 だから,図の中の直角三角形を考えると答えが出せるよ。
だから,図の中の直角三角形を考えると答えが出せるよ。
物理が苦手な文子
本当だ。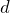 を含む直角三角形を考えると,こうなるわね。
を含む直角三角形を考えると,こうなるわね。
![]()
物理が得意な秀樹
そういうことだね。答えは②だ。