■点電荷のまわりの電場(電界)
物理が苦手な文子
電場の向きを求める問題ね。
物理が得意な秀樹
点電荷が作る電場の向きについては,分かってる?正電荷と負電荷でちょっと違うけど。
物理が苦手な文子
こんな感じだっけ?
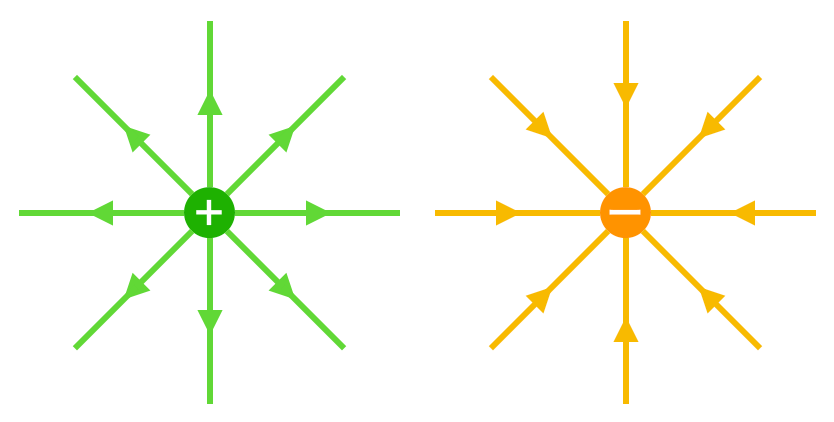
物理が得意な秀樹
そうだね。この感じでいいんだけど,この線のことは「電気力線(でんきりきせん)」っていうんだよね。
物理が苦手な文子
「でんきりょくせん」じゃなくて「でんきりきせん」ね。
物理が得意な秀樹
そう。今は電場を考えるので,例えば下の図で考えてみよう。正電荷と負電荷が点Oにつくる電場の向きは分かるかな?
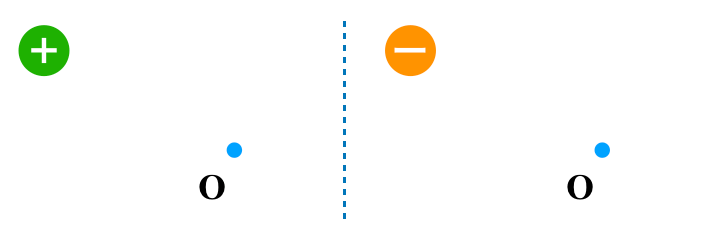
物理が苦手な文子
最初に描いた図を参考にすればいいのよね。
物理が得意な秀樹
そうだね。あくまでも点Oの電場の向きね。
物理が苦手な文子
これでいいわよね。
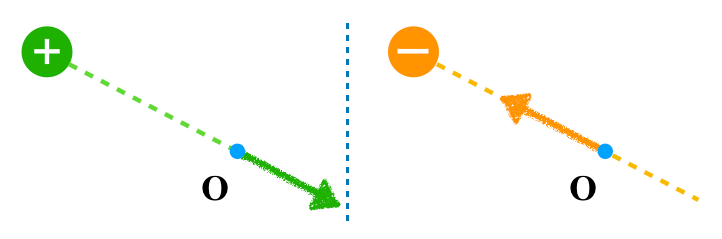
物理が得意な秀樹
それでいいね。電場の向きに関してはこれでいいので,もう一つ,点電荷がつくる電場の強さはどう表されるか覚えてる?
物理が苦手な文子
なんとなく覚えてるけど,似たような式がいろいろあるのよね。
■点電荷に関する公式の確認
物理が得意な秀樹
そうなんだよね。ここでまとめておこうか。

物理が苦手な文子
やっぱりややこしいわ。
物理が得意な秀樹
確かにややこしいね。ややこしいけど,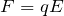 と
と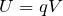 という関係があるから,うまく組み合わせると少しは覚えやすくなると思うよ。
という関係があるから,うまく組み合わせると少しは覚えやすくなると思うよ。
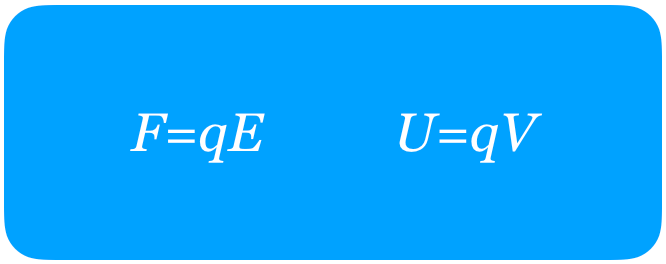
物理が苦手な文子
なるほど,そう考えると少しは整理できるわね。今は電場の強さを求めたいので,
![]()
を使えばいいのね。
■4つの点電荷による電場の合成
物理が得意な秀樹
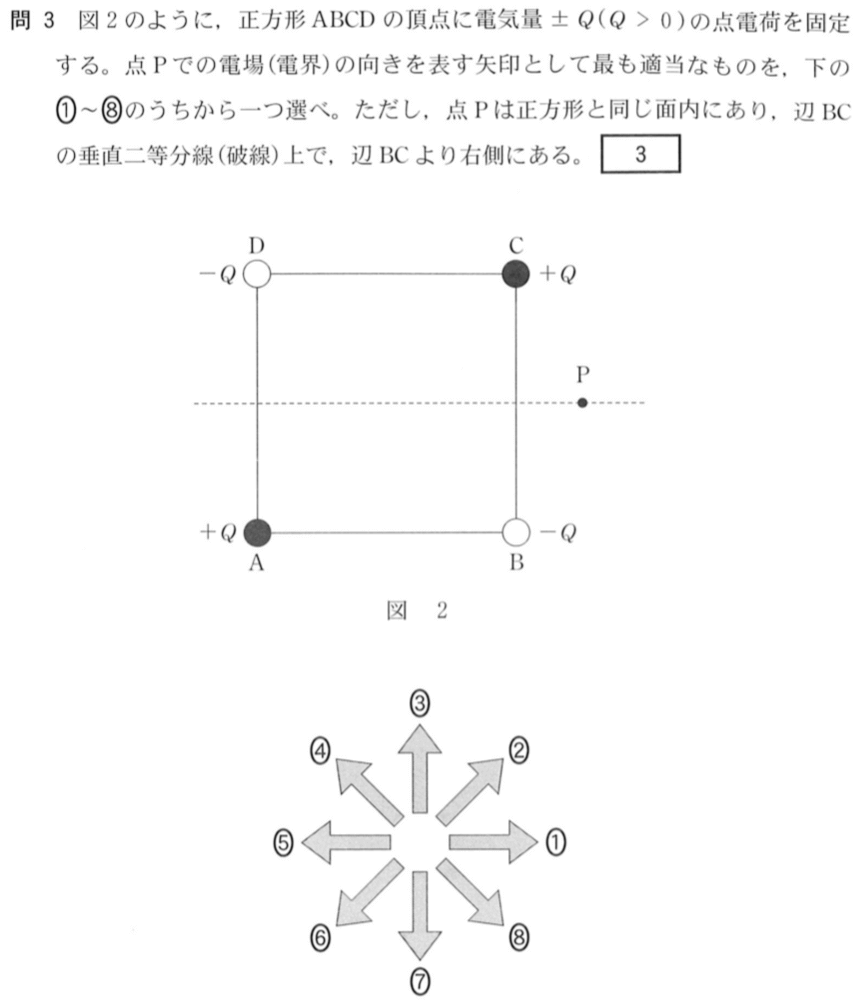
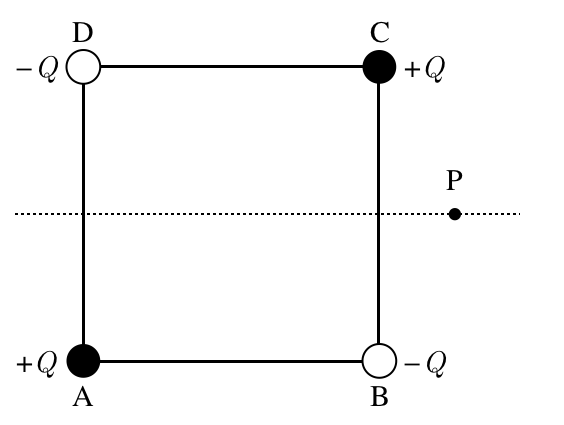
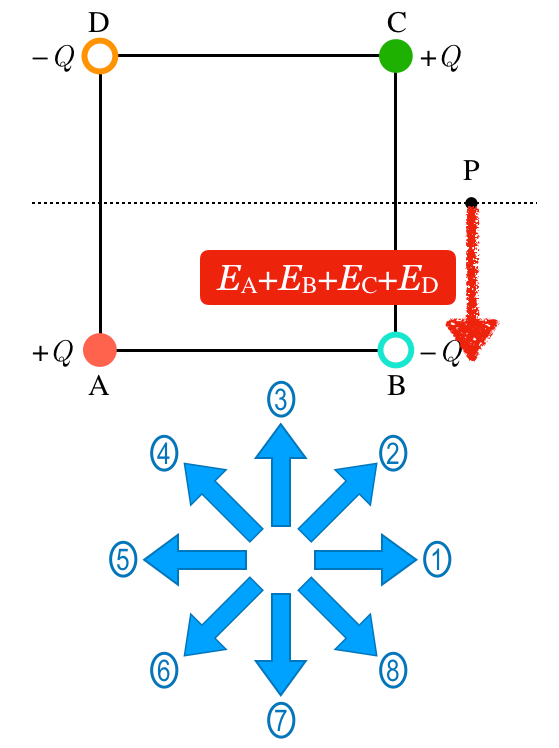
そうだね。ここで大切なのは「電場の強さは点電荷からの距離の二乗に反比例する」っていうことだよ。それではまず図を描いてみようか。求めたいのはこの図の点Pの電場の向きだね。
物理が苦手な文子
電荷が4つもあるので,どうすればいいか分からないわ。
物理が得意な秀樹
4つの電荷を合わせて考えるよりも,1つずつ順番に考えてみようか。点Cの電荷が点Pにつくる電場はどうなるかな?
物理が苦手な文子
点Cにあるのは正電荷なので,こんな感じね。
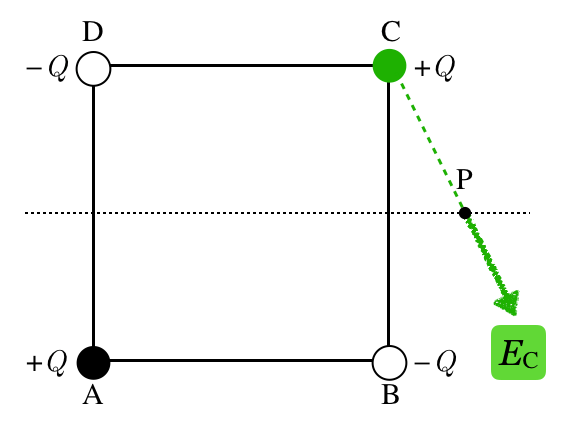
物理が得意な秀樹
いいね。点A,B,Dについても描いてみようか。ちなみに,点BとCはPまでの距離は同じだけど,点AとDはPまでの距離が長いよね。
物理が苦手な文子
ということは,点AとDがつくる電場の矢印を短くすればいいのね。矢印が4本になるけど,描くわね。
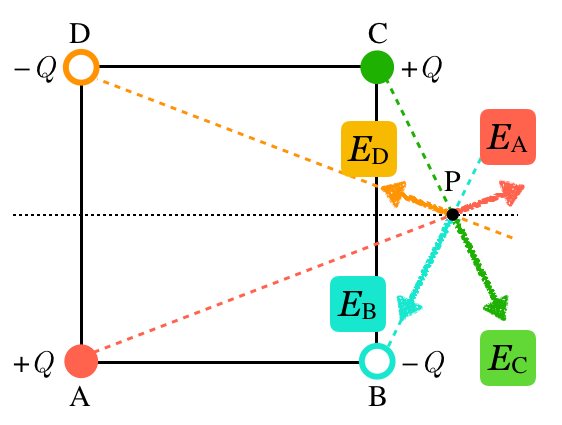
物理が得意な秀樹
素晴らしい。この4本の矢印を合わせたのが答えだ。
物理が苦手な文子
4本の矢印をベクトルとして和を求めるのね。矢印が4本もあるし,角度もよくわからないので難しいわ。
物理が得意な秀樹
4本の矢印を2本ずつに分けて考えるといいよ。
物理が苦手な文子
どう分ければいいの?
物理が得意な秀樹
上向きの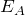 と
と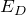 ,下向きの
,下向きの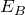 と
と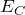 という組み合わせがいいね。
という組み合わせがいいね。
物理が苦手な文子
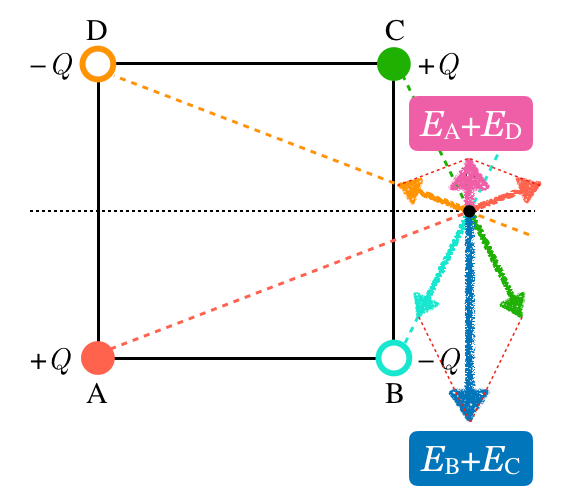
なるほど。そう組合わせてベクトルの足し算をすると,こうなるわね。
物理が得意な秀樹
そうだね。あとは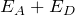 と
と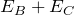 を足し算すればいいね。
を足し算すればいいね。
物理が苦手な文子
こういうことね。
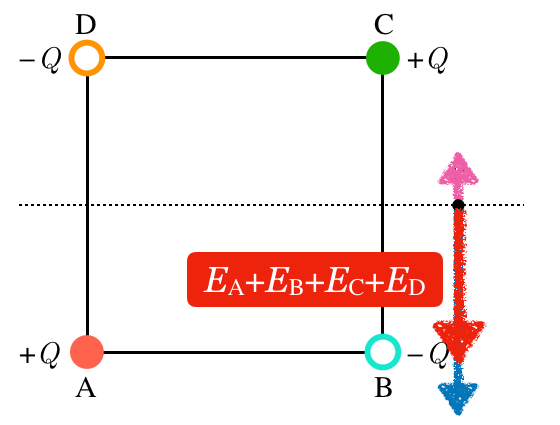
物理が得意な秀樹
ということは,答えはどうなるかな?
物理が苦手な文子
問題の選択肢の矢印の中から下向きを選べばいいので,答えは⑦ね。
物理が得意な秀樹
正解だ!