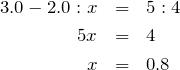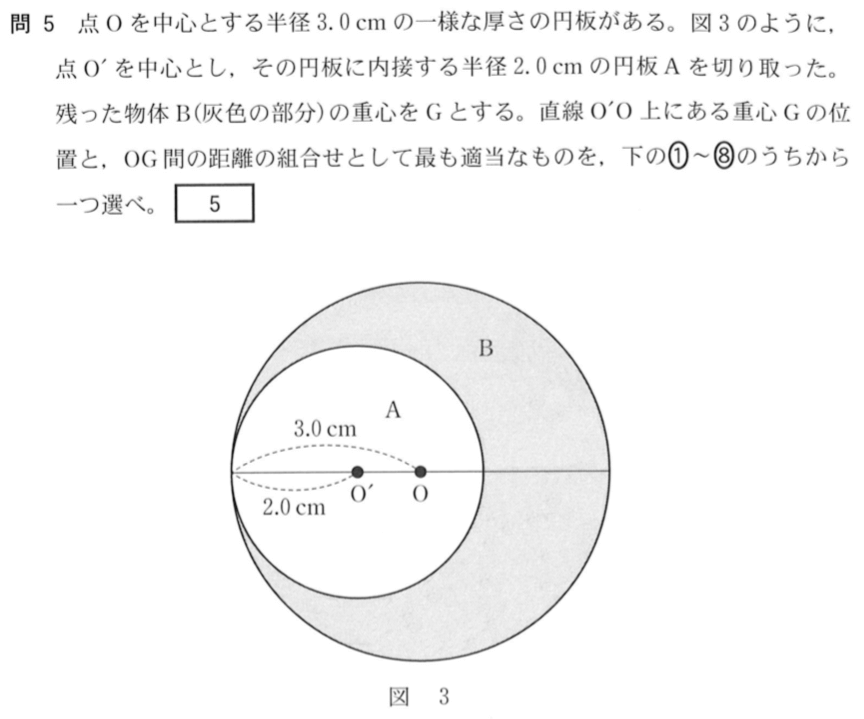
■重心の位置は見た目でだいたい分かる
三日月形の重心を求める問題ね。見たことある感じがするんだけど・・・
切り取った円の部分がもう少し小さい問題はよくあるよね。でも大きくても小さくてもやり方は一緒だ。
とりあえず,まずは重心Gの位置が点Oの右か左かを考えようか。まぁ,考えるというよりも,見たら分からないかな。

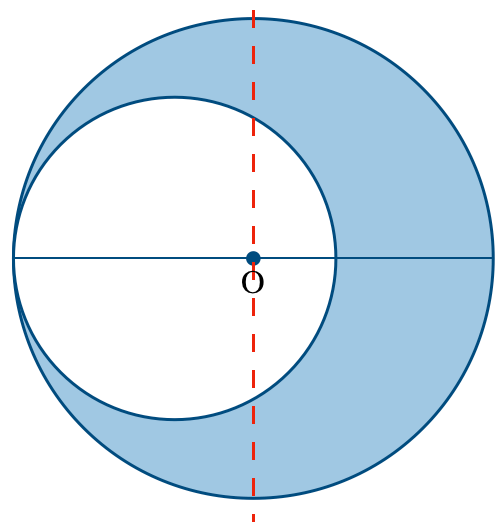
縦に線を入れてみると分かりやすいですね。明らかに点Oよりも右側の面積が大きいから,重心Gは点Oの右側ね。
■AとBを合わせた重心は大きな円の中心
そうだね。それでは実際に重心の場所を求めてみようか。
まず,三日月形Bの重心Gの位置をOの右側

[cm]のところにするよ。
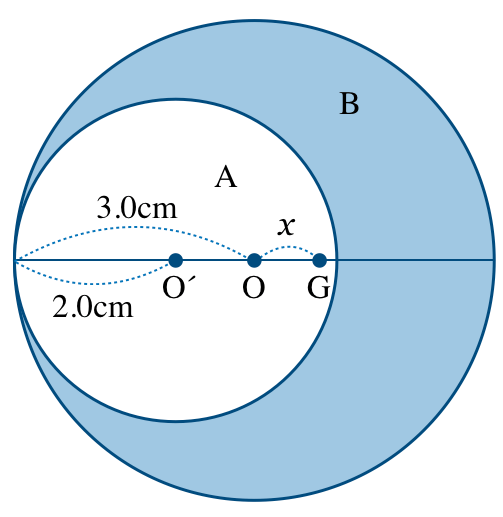
あれ?Bの重心Gが三日月形の板上にないけどいいの?
例えば,穴のあいたドーナツの重心は,ドーナツ上ではなく穴の真ん中にあるんだ。だから,三日月形の重心も三日月の上になくてもいいんだよ。
なるほど,分かったわ。それじゃあ,この

を求めればいいのね。
そう。で,やり方なんだけど,切り取った円板を元に戻すことを考えるんだ。
切り取った小さな円板Aと,切り取られた三日月形の板B合わせると元の大きな円板になるよね。
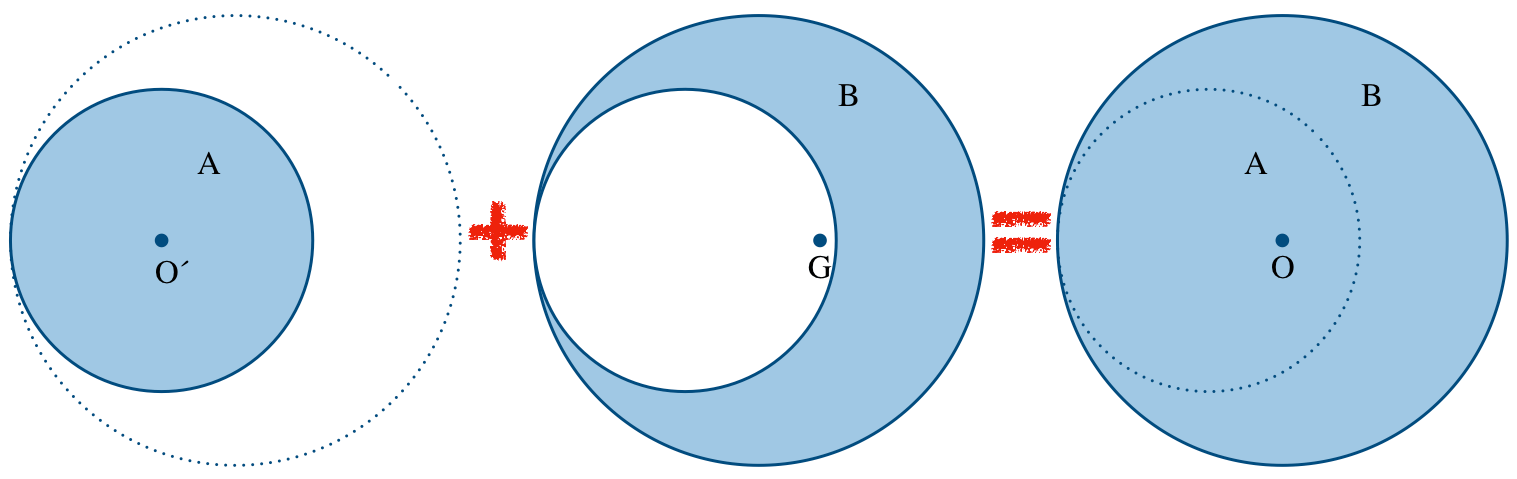
重心の位置を考えると,Aは円なので,重心は円の中心O

,Bの重心は今求めたいG,AとBを合わせた大きな円の重心はOだよね。
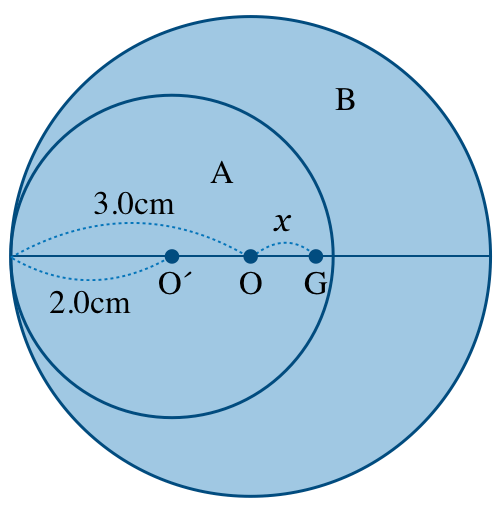
これって,2つの物体を合わせたときの重心の話だよね。
AとBの2つの物体ね。確か2つの物体を合わせたときの重心って,何か公式があったわよね。
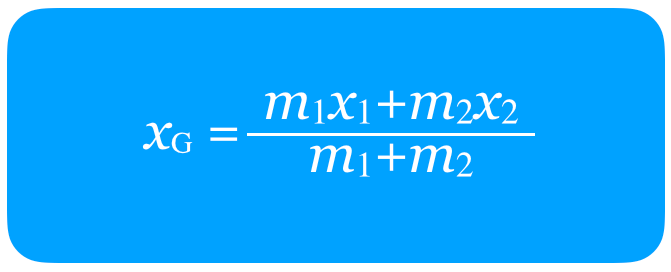
もちろんこの式を使ってもできるんだけど,今は基本的な考え方でやろう。「重心」っていうのは「重さの中心」っていうことだから,まずはAとBの重さの比を求めるんだ。
■重さの比は面積の比
急に重さを求めると言われても,重さに関する情報が何も無いわ。
「重さ」を求めるんじゃなくて,「重さの比」が分かればいいんだ。問題文に「一様な厚さの円板」ってあるでしょ。
厚さが一様だということは,
重さの比 = 面積の比
っていうことなんだよ。
なるほど。ということは,AとBの面積の比を求めればいいのね。
まず,円Aの面積は,
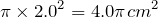
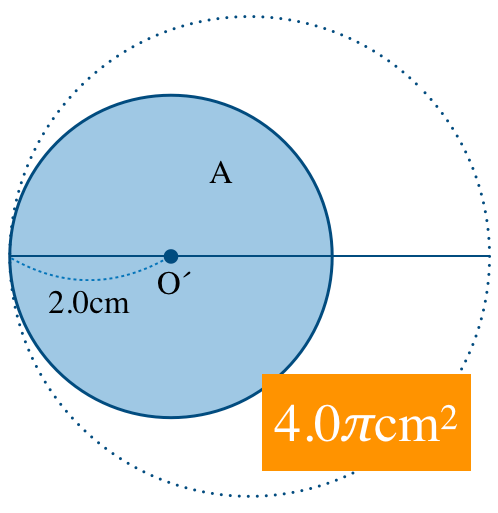
大きな円の面積は,
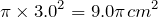
だから,三日月形Bの面積は,
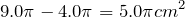
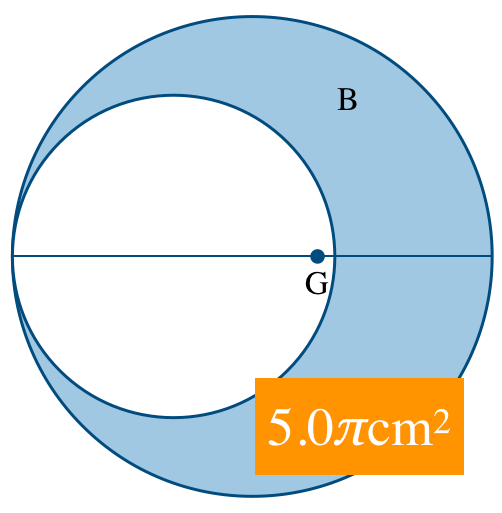
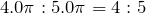
ね。
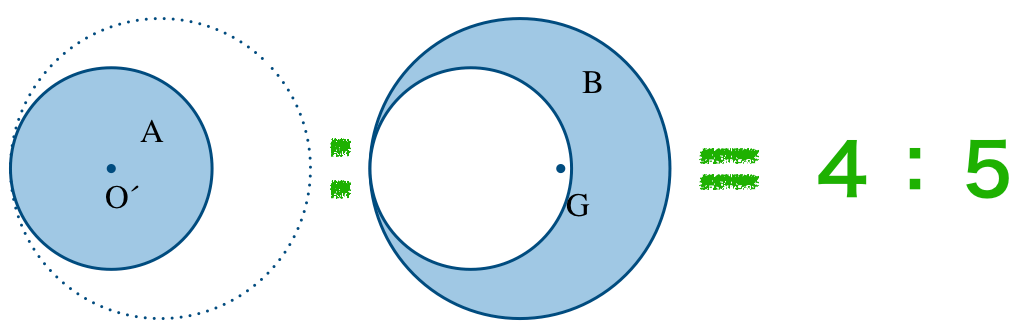
これで面積の比が分かったから,重さの比も
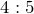
だね。
そうすると,重さの関係を図にするとこんな感じになるんだ。
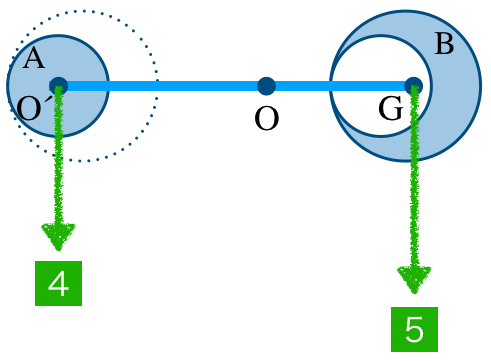
なるほど。O

にはたらく力の大きさが4,Gにはたらく力の大きさが5ということね。
そう。物体の重さは重心にはたらく力だと考えていいんだよね。とすると,このAとBの2つの重さを1つに合わせると,大きな円の中心Oに来るんだよね。そしてそのOは,Aの重さとBの重さの逆比,つまり5:4の位置に来るはずなんだ。
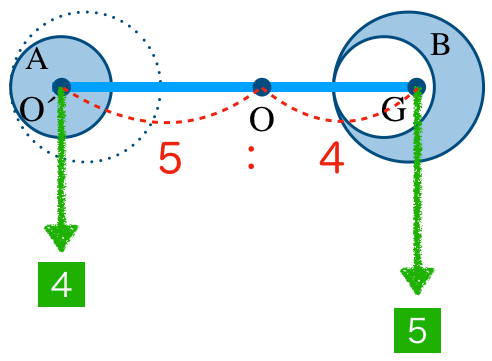
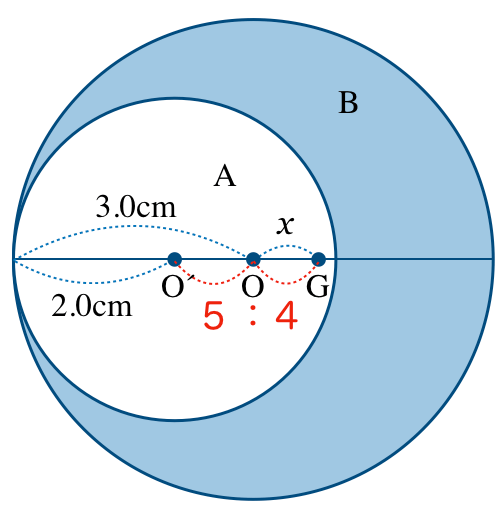
そうか,こうなるのね。ここまでくれば,図を見て簡単に式を立てれるわね。
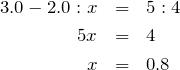
その通り。まとめると,Bの重心は「Oの右側0.8cm」のところとなって,答えは②だ。




![]() [cm]のところにするよ。
[cm]のところにするよ。
![]() を求めればいいのね。
を求めればいいのね。
![]() ,Bの重心は今求めたいG,AとBを合わせた大きな円の重心はOだよね。
,Bの重心は今求めたいG,AとBを合わせた大きな円の重心はOだよね。
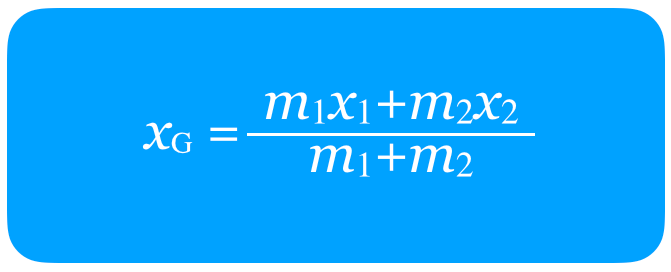
![]()

![]()
![]()

![]() ね。
ね。
![]() だね。
だね。
![]() にはたらく力の大きさが4,Gにはたらく力の大きさが5ということね。
にはたらく力の大きさが4,Gにはたらく力の大きさが5ということね。

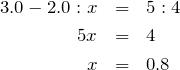
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!



![]() [cm]のところにするよ。
[cm]のところにするよ。
![]() を求めればいいのね。
を求めればいいのね。
![]() ,Bの重心は今求めたいG,AとBを合わせた大きな円の重心はOだよね。
,Bの重心は今求めたいG,AとBを合わせた大きな円の重心はOだよね。
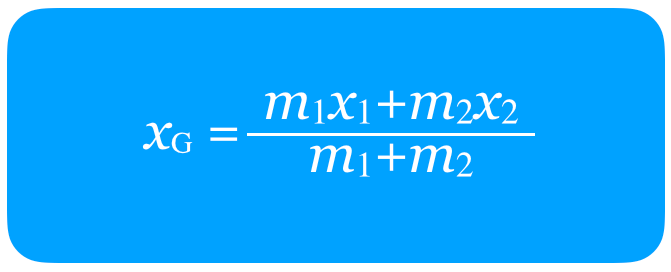
![]()

![]()
![]()

![]() ね。
ね。
![]() だね。
だね。
![]() にはたらく力の大きさが4,Gにはたらく力の大きさが5ということね。
にはたらく力の大きさが4,Gにはたらく力の大きさが5ということね。