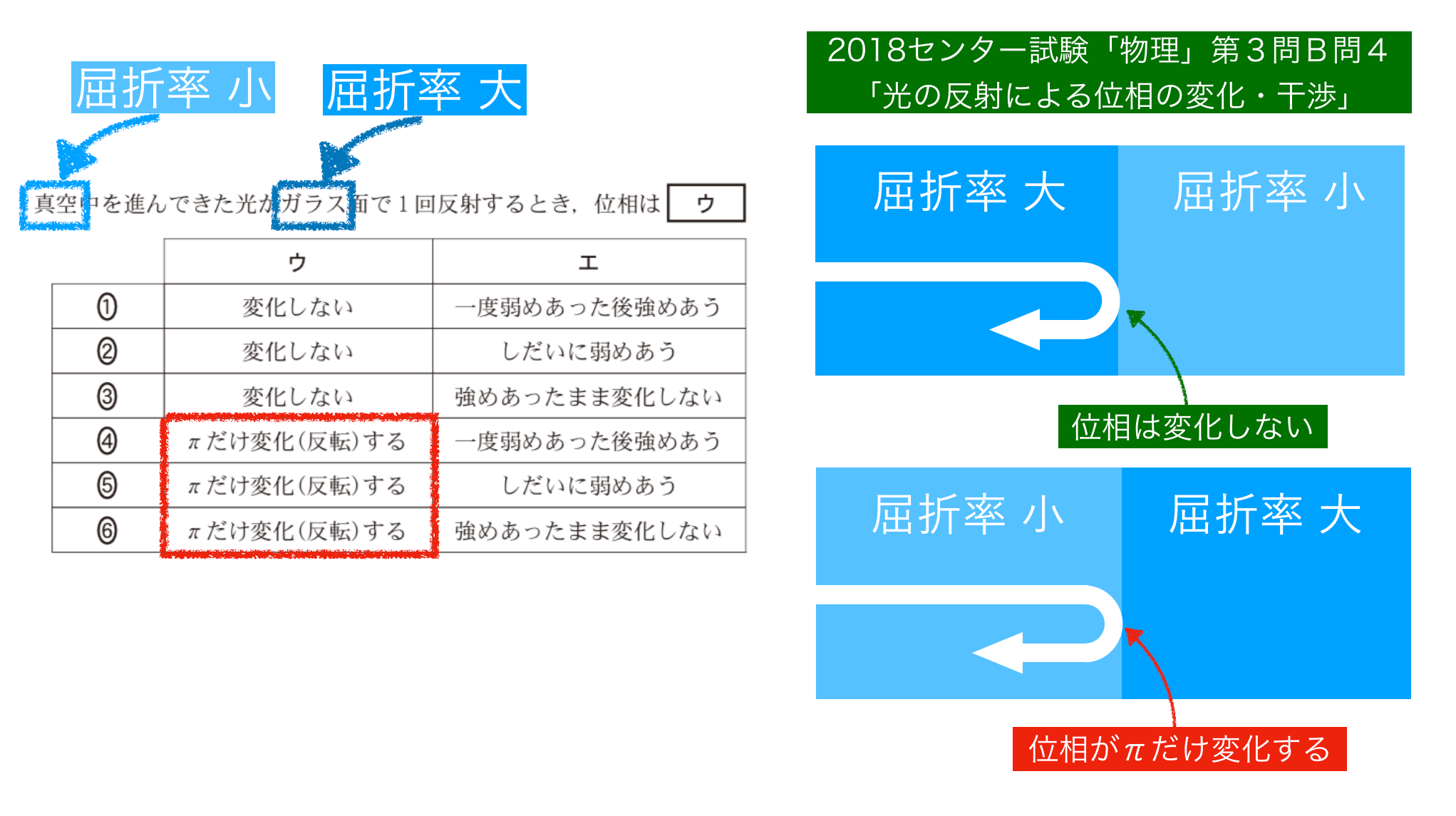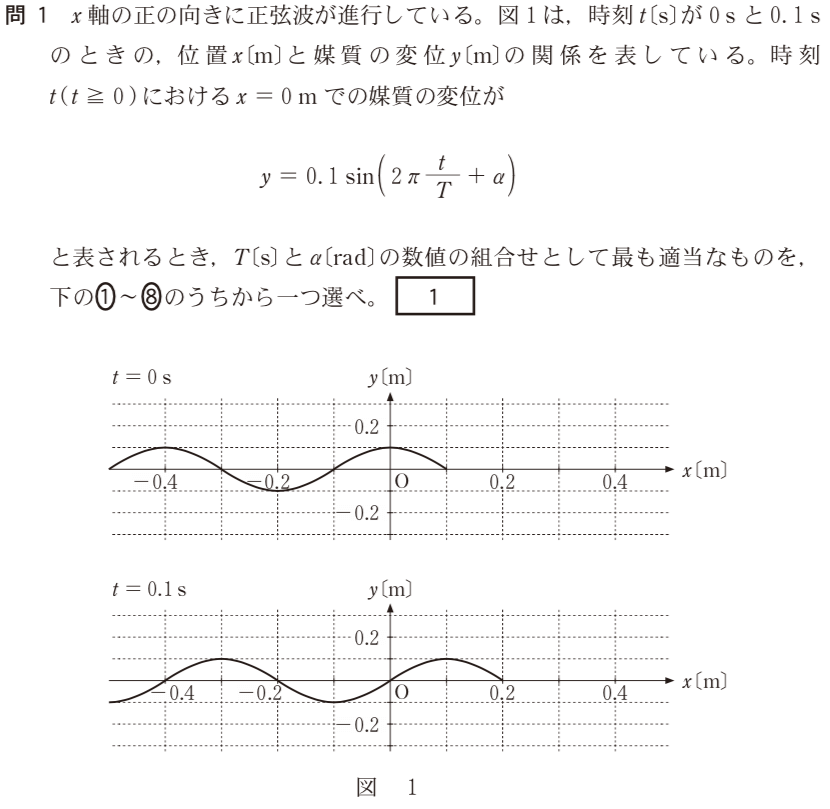
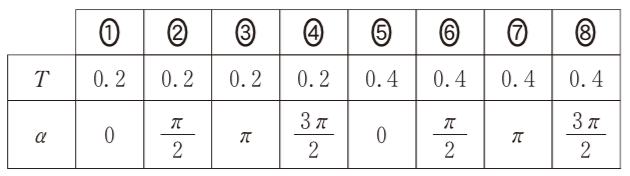
■波の式に頼らずに考えてみる
sinの中にある

と
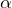
を求めると言われても,何をすればいいか分からない。
この

は,周期を表す

だから,周期を求めればいいんだよ。
波の分野に出てくる

が周期を表すのは知ってるけど,式の中の

が周期を表しているのは気が付かないわ。
なるほど。波の式を覚えていれば,分かるんだけどね。こんな式だよ。
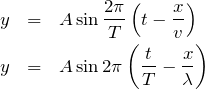
見たことはあるけど・・・,この式から
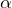
も分かるの?
実は分からないんだよ。問題の波の式は

=0mでの媒質の変位を表しているので,

=0を波の式に代入してみるよ。この場合はどっちの式に代入しても同じだね。
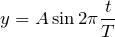
こんな風になっちゃうんだよ。
それじゃあ,
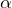
=0でしょ。
それが違うんだよ。この問題では与えられた式を変形するというよりは,問題の下にあるグラフから条件を読み取るんだ。
そうか,グラフが2つもあるわね。どうすればいいの?
2つのグラフからいろんな情報を読み取ることができるんだけど,問題の波の式は

=0mでの媒質の変位だったから,

=0mの情報を読み取ろう。
なるほどね。

=0sのグラフを見ると,

=0mで
=0.1mね。
そうだね。

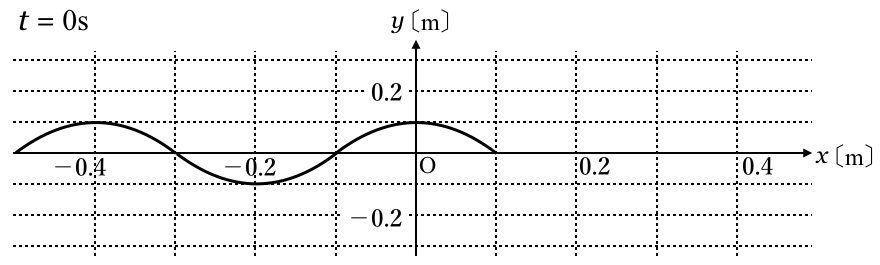
=0.1sのグラフは?
そう,それじゃあ

=0sの情報を問題の式に代入してみよう。

=0で
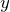
=0.1なので,
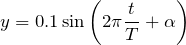
に代入すると,
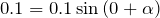
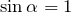
ということは,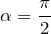 でいいの?
でいいの?
三角関数は2
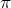
ごとに同じ値を取るから,実際には
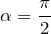
だけではないんだけど,選択肢を見ると該当するのは
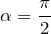
しかないんだよね。
なるほどね。これで
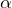
は分かったけど,

はどうすればいいの?
やっぱり次は,

=0.1sの情報を問題の式に代入してみようよ。
そう言えばそうだったわね。

=0.1で
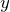
=0と,
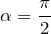
を,
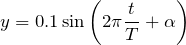
に代入すると,
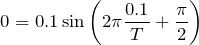
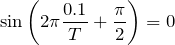
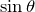
が0になるのは,
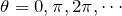
といろいろあるわよね。どうすればいい?
順番に計算していけば,いつか答えが出ると思うけど,今は選択肢を見ると
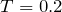
か
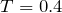
しかないから,両方代入してみれば成り立つ方が分かるんじゃない?
あっ,そうね。それじゃあまず,
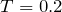
を代入してみると,
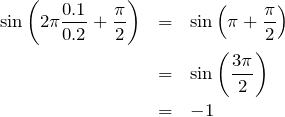
0にならなかったから,
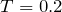
は違うみたいだね。
じゃあ
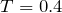
が答えね。
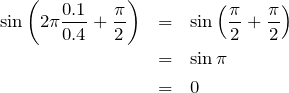
やっぱり0になったね。まとめると,
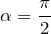
,
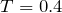
なので,答えは⑥だ。それでは問2にいってみよう。
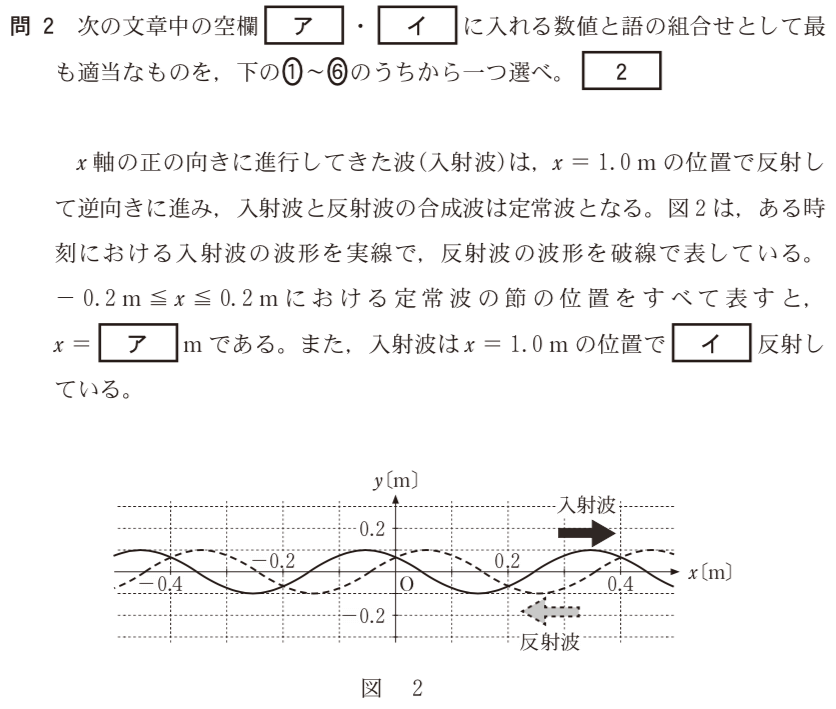
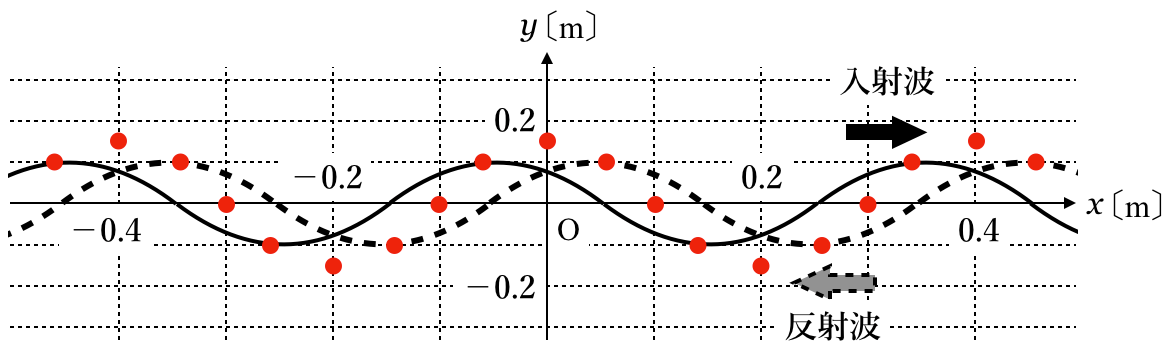
■合成波を描いてみる
この問題では,

=1.0mで反射したって書いてあるけど,図には

=1.0mは無いわね。
そこまで図はなくても,問題は解けるっていうことかな。まぁ必要だったら波形を伸ばせばいいよね。
そうね。問題を読むと図の入射波と反射波から合成波を描けば良さそうだけど,それでいい?
そうだね。まずはこの入射波と反射波の波形をもとに合成波を描いてみよう。
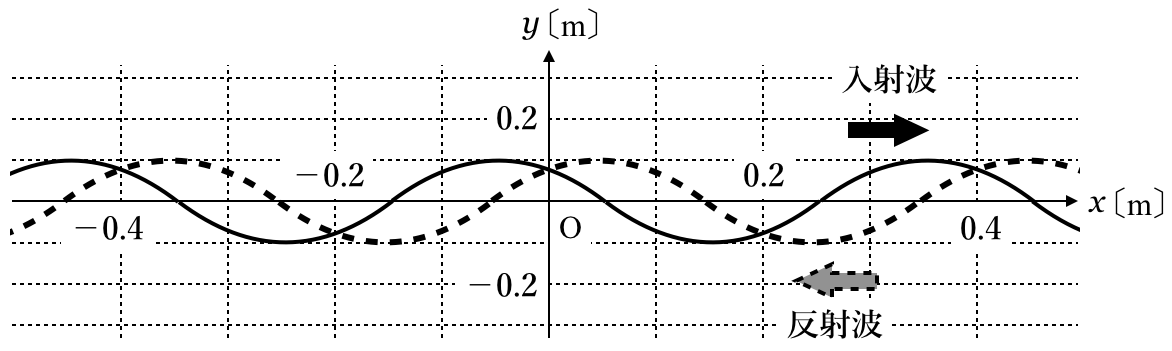
最初は点をとってみるわ。入射波と反射波の変位の和をとった点ね。
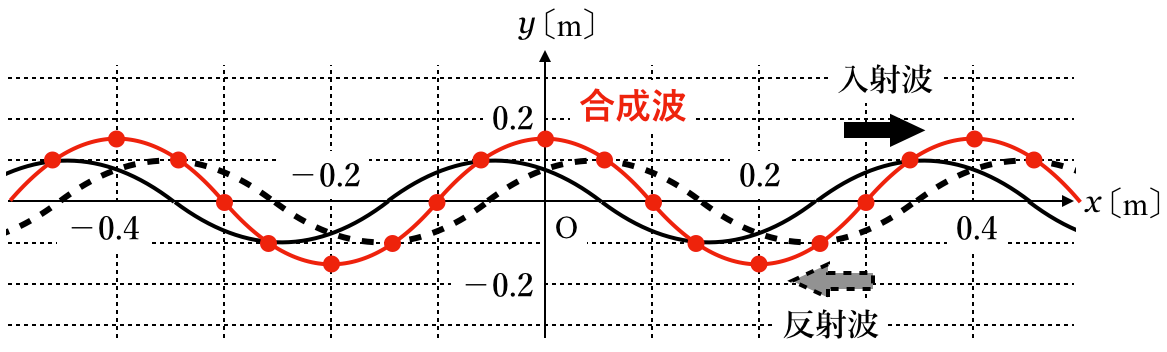
■腹の位置と節の位置を確認する
定常波の腹や節を見つけるのって,定常波を動かしてみないと分からないんだっけ?
そんなことないよ。今描いた合成波を見れば節の位置はすぐに分かるよ。
ということは,

軸と交わっているところ?
そうだよ。節は動かないから節なんだよね。だから,この瞬間に変位
=0だったら,時間が経っても
=0なんだよ。
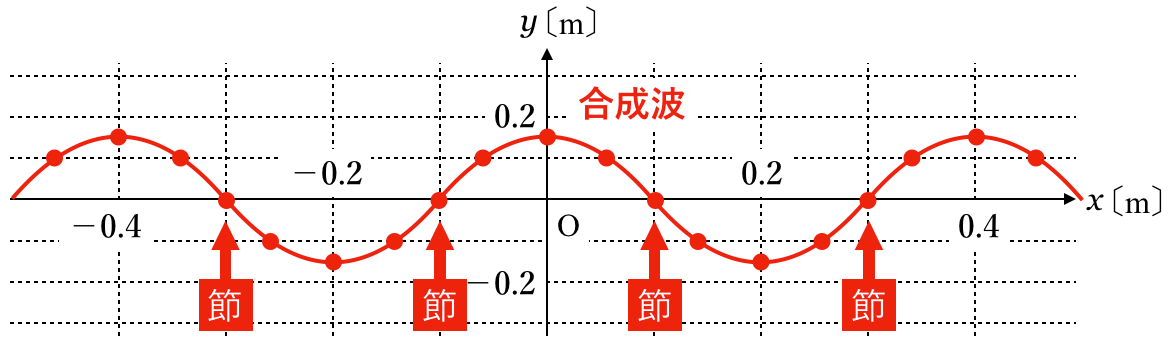
いいね。ただ,今は−0.2m≦

≦0.2mなので,この範囲に入る節の位置は−0.1mと0.1mだね。
節の位置が分かったら,あとは

=1.0mが,固定端反射なのか,自由端反射なのかね。やっぱり

=1.0mまで波形を伸ばしたほうがいいの?
伸ばしてもいいけど,伸ばす必要はないんだ。固定端反射,自由端反射と定常波の腹,節の関係は覚えてる?
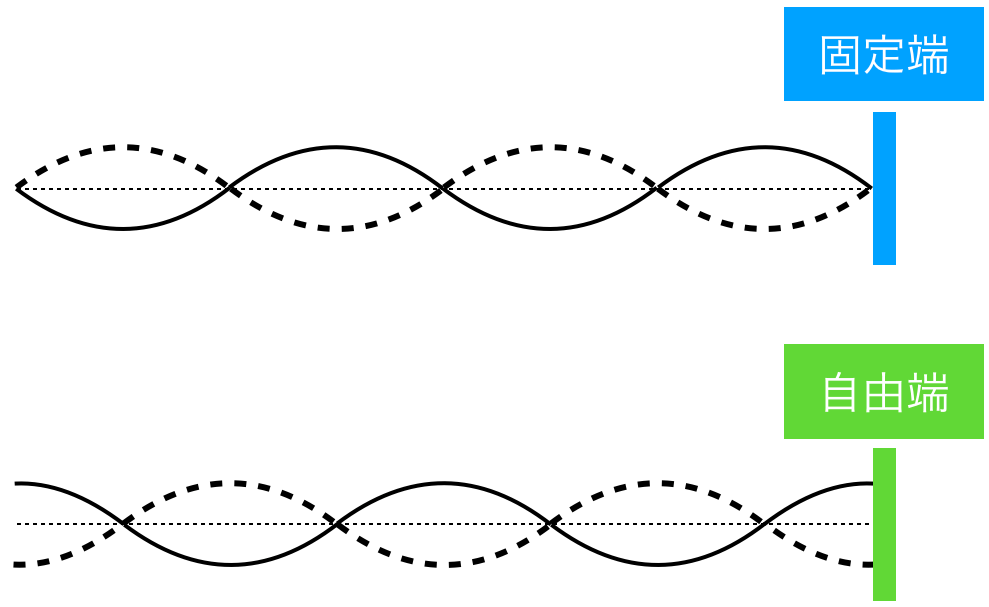
それじゃあ,

=1.0mのところが腹なのか,節なのかが分かればいいのね。
もう節の場所は分かっているし,節と節の間に腹が来るから

=1.0mの位置が腹なのか節なのかは分かりそうだよね。
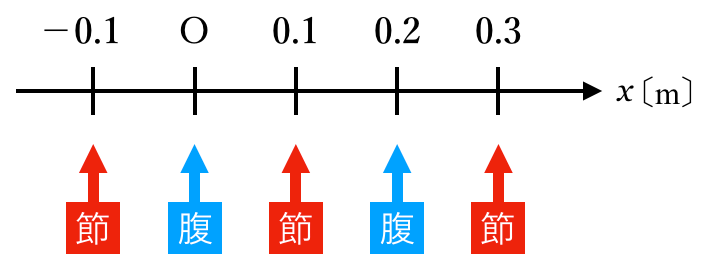
このままいくと,

=1.0mの位置は腹になりそうね。
つまり,

=1.0mが腹ということは,自由端反射をしているのね。
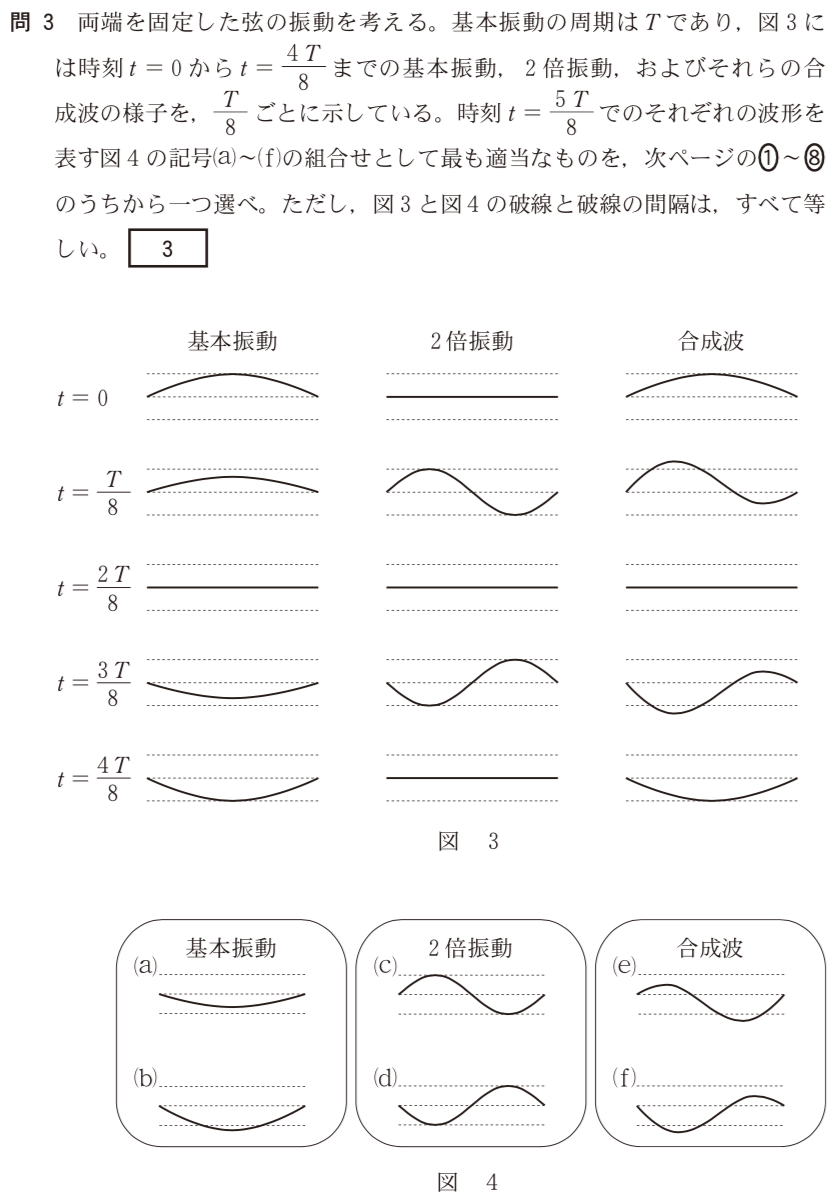
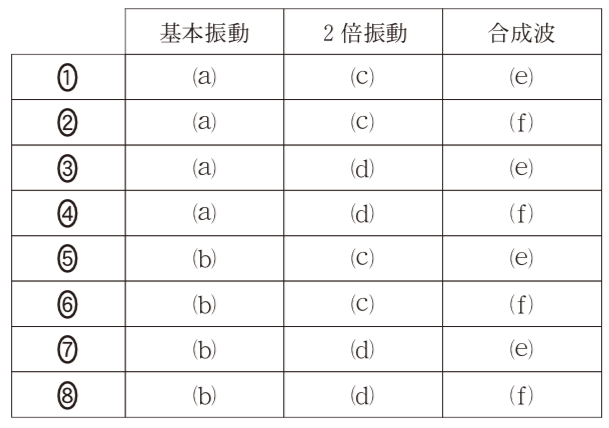
■基本振動と2倍振動の合成波を考える
今度は弦の振動の問題ね。基本振動と2倍振動は分かるけど,合成波ってどういうこと?
そうだね。普通「合成波」と言ったら,今やった問2のように,逆向きに進む2つの進行波がぶつかったときに,重ね合わせて考えるんだね。例えば,この問題の基本振動や2倍振動も,右向きの波と,左向きの波が合成されてできているんだね。
弦の振動も気柱に生じる固有振動も,定常波ができていて,定常波は合成波なんだ。
この問題では,基本振動と2倍振動を合成した「合成波」を考えているんだ。
そういうことになるね。ややこしそうだけど,考え方は簡単だよ。基本振動の波形と2倍振動の波形を合成するのは,問2でやった定常波を求める方法と同じだ。
そもそも,問題の図には合成波が描かれているけど,これは基本振動と2倍振動の波形を合成したっていうこと?
そうだよ,確認してみようか。1つの図にまとめちゃった方が分かりやすいよね。
確かに合成波の波形は,基本振動と2倍振動の波形を合成した波形になっているわね。この問題で求めたいのは,
のときだから,この次の時刻の波形ね。
■t=0sの基本振動の波形は,変位が最大のときなのか?
で弦の中央の変位が最大になっているから,
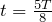
では上に戻って(a)の波形になると思うんだけどどう?
答えは合ってるんだけど,どうして(b)じゃないの?
だって,
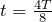
で変位が最大でしょ。
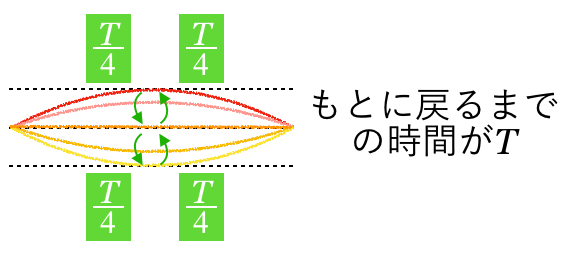
実は問題文に大切なことが書かれていて,「基本振動の周期は

」とあるでしょ。つまり,
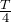
ごとに「変位最大」と「変位0」を繰り返すんだ。だから,
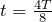
で変位が最大になっているので,次の瞬間上に戻るんだね。
というわけで,
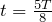
での基本振動の波形は少し戻った波形,(a)だ。それでは2倍振動はどうかな。
弦全体の変位が0になっている時刻が3つもあるわね。周期が

だとすると,おかしくない?
おかしくないんだな。問題文にあるのは,「基本振動の周期は

」だよ。
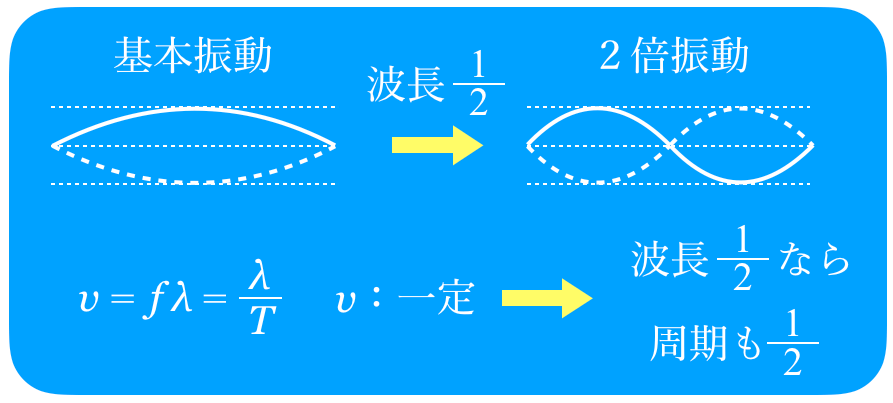
変わらないのが弦を伝わる波の速さ

で,波長と周期,振動数は変わるね。2倍振動の波長は基本振動の波長の半分だから,
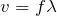
より,振動数は2倍になって,
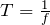
だから,周期は半分になるね。
2倍振動では周期が半分だから,問題の図の

=0から

=
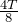
までで,1周期ということね。
ということは,
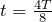
までで1周期が終わっているから,
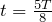
は戻って次の時刻だから
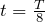
と同じ波形の(c)が答えね。
その通り。では基本振動である(a)の波形と2倍振動の(c)の波形を合成してみようか。
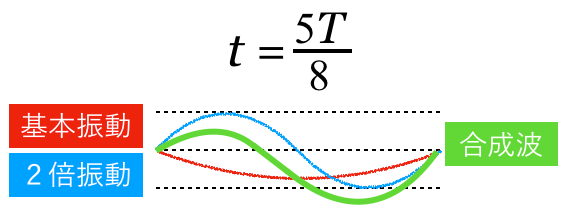
正解だ。選択肢から選ぶと合成波は(e)の波形になるので,「(a),(c),(e)」という答えは①だ。


![]() と
と![]() を求めると言われても,何をすればいいか分からない。
を求めると言われても,何をすればいいか分からない。![]() は,周期を表す
は,周期を表す![]() だから,周期を求めればいいんだよ。
だから,周期を求めればいいんだよ。![]() が周期を表すのは知ってるけど,式の中の
が周期を表すのは知ってるけど,式の中の![]() が周期を表しているのは気が付かないわ。
が周期を表しているのは気が付かないわ。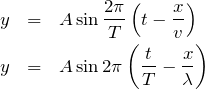
![]() も分かるの?
も分かるの?![]() =0mでの媒質の変位を表しているので,
=0mでの媒質の変位を表しているので,![]() =0を波の式に代入してみるよ。この場合はどっちの式に代入しても同じだね。
=0を波の式に代入してみるよ。この場合はどっちの式に代入しても同じだね。
![]()
![]() =0でしょ。
=0でしょ。![]() =0mでの媒質の変位だったから,
=0mでの媒質の変位だったから,![]() =0mの情報を読み取ろう。
=0mの情報を読み取ろう。
![]() =0sのグラフを見ると,
=0sのグラフを見ると,![]() =0mで
=0mで![]() =0.1mね。
=0.1mね。![]() =0.1sのグラフは?
=0.1sのグラフは?
![]() =0.1sのグラフは,
=0.1sのグラフは,![]() =0mで
=0mで![]() =0mね。
=0mね。![]() =0sの情報を問題の式に代入してみよう。
=0sの情報を問題の式に代入してみよう。![]() =0で
=0で![]() =0.1なので,
=0.1なので,![]() に代入すると,
に代入すると,
![]()
![]()
![]() でいいの?
でいいの?![]() ごとに同じ値を取るから,実際には
ごとに同じ値を取るから,実際には![]() だけではないんだけど,選択肢を見ると該当するのは
だけではないんだけど,選択肢を見ると該当するのは![]() しかないんだよね。
しかないんだよね。![]() は分かったけど,
は分かったけど,![]() はどうすればいいの?
はどうすればいいの?![]() =0.1sの情報を問題の式に代入してみようよ。
=0.1sの情報を問題の式に代入してみようよ。![]() =0.1で
=0.1で![]() =0と,
=0と,![]() を,
を,![]() に代入すると,
に代入すると,![]()
![]()
![]() か
か![]() しかないから,両方代入してみれば成り立つ方が分かるんじゃない?
しかないから,両方代入してみれば成り立つ方が分かるんじゃない?![]() を代入してみると,
を代入してみると,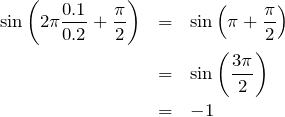
![]() は違うみたいだね。
は違うみたいだね。![]() が答えね。
が答えね。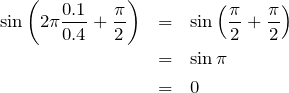
![]() ,
,![]() なので,答えは⑥だ。それでは問2にいってみよう。
なので,答えは⑥だ。それでは問2にいってみよう。

![]() =1.0mで反射したって書いてあるけど,図には
=1.0mで反射したって書いてあるけど,図には![]() =1.0mは無いわね。
=1.0mは無いわね。


![]() 軸と交わっているところ?
軸と交わっているところ?![]() =0だったら,時間が経っても
=0だったら,時間が経っても![]() =0なんだよ。
=0なんだよ。
![]() ≦0.2mなので,この範囲に入る節の位置は−0.1mと0.1mだね。
≦0.2mなので,この範囲に入る節の位置は−0.1mと0.1mだね。![]() =1.0mが,固定端反射なのか,自由端反射なのかね。やっぱり
=1.0mが,固定端反射なのか,自由端反射なのかね。やっぱり![]() =1.0mまで波形を伸ばしたほうがいいの?
=1.0mまで波形を伸ばしたほうがいいの?
![]() =1.0mのところが腹なのか,節なのかが分かればいいのね。
=1.0mのところが腹なのか,節なのかが分かればいいのね。![]() =1.0mの位置が腹なのか節なのかは分かりそうだよね。
=1.0mの位置が腹なのか節なのかは分かりそうだよね。
![]() =1.0mの位置は腹になりそうね。
=1.0mの位置は腹になりそうね。![]() =1.0mが腹ということは,自由端反射をしているのね。
=1.0mが腹ということは,自由端反射をしているのね。


![]() のときだから,この次の時刻の波形ね。
のときだから,この次の時刻の波形ね。![]() で弦の中央の変位が最大になっているから,
で弦の中央の変位が最大になっているから,![]() では上に戻って(a)の波形になると思うんだけどどう?
では上に戻って(a)の波形になると思うんだけどどう?![]() で変位が最大でしょ。
で変位が最大でしょ。![]() 」とあるでしょ。つまり,
」とあるでしょ。つまり,![]() ごとに「変位最大」と「変位0」を繰り返すんだ。だから,
ごとに「変位最大」と「変位0」を繰り返すんだ。だから,![]() で変位が最大になっているので,次の瞬間上に戻るんだね。
で変位が最大になっているので,次の瞬間上に戻るんだね。
![]() での基本振動の波形は少し戻った波形,(a)だ。それでは2倍振動はどうかな。
での基本振動の波形は少し戻った波形,(a)だ。それでは2倍振動はどうかな。![]() だとすると,おかしくない?
だとすると,おかしくない?![]() 」だよ。
」だよ。![]() で,波長と周期,振動数は変わるね。2倍振動の波長は基本振動の波長の半分だから,
で,波長と周期,振動数は変わるね。2倍振動の波長は基本振動の波長の半分だから,![]() より,振動数は2倍になって,
より,振動数は2倍になって,![]() だから,周期は半分になるね。
だから,周期は半分になるね。
![]() =0から
=0から![]() =
=![]() までで,1周期ということね。
までで,1周期ということね。![]() までで1周期が終わっているから,
までで1周期が終わっているから,![]() は戻って次の時刻だから
は戻って次の時刻だから![]() と同じ波形の(c)が答えね。
と同じ波形の(c)が答えね。