この問題の5つのポイント
- スカラーは大きさのみ，ベクトルは大きさと向きを持った物理量
- 運動エネルギーはスカラー，運動量はベクトル
- どんな衝突でも運動量の和は保存される
- 運動エネルギーと仕事，運動量と力積
- 等速円運動は「速度が一定の円運動」ではない！
1. スカラーは大きさのみ，ベクトルは大きさと向きを持った物理量
「スカラー」と「ベクトル」は，習い始めのときは「何でわざわざ向きのある・なしで区別するんだろう？」程度の認識だったかもしれません。しかしこの問題のように，しっかりと認識していないと間違ってしまうことがあるので，とりあえず力学の分野に出てくる代表的な物理量をスカラーとベクトルに分けておきます。（ちなみにこの問題の誤答として多かったのは「④等速円運動する物体の運動量は一定である」だったようです。）
この問題に登場する運動エネルギーはスカラー，運動量はベクトルです。
2. 運動エネルギーはスカラー，運動量はベクトル
表にまとめた通り，エネルギーはスカラーなので，もちろん「運動エネルギー」もスカラーです。運動している物体は当然運動の向きを持っているので，その向きの運動エネルギーというものを持っていそうですが，右向きであろうと左向きであろうと，上向きであろうと斜め方向を向いていようと，運動エネルギーは向きを持っていません。
つまり，選択肢の①は間違っているということになります。
一方，運動量はベクトルなので向きを持っていて，同じ大きさでも右向きと左向きでは別の運動量ということになります。
3. どんな衝突でも運動量の和は保存される
２つの物体が衝突する場合，衝突の前後で運動量の和は常に保存されます。一方，運動エネルギーは弾性衝突（反発係数
の衝突）では保存されますが，それ以外の衝突では減少します。反発係数の値によって，まとめてみます（「完全非弾性衝突」は「非弾性衝突」の特別な場合です）。
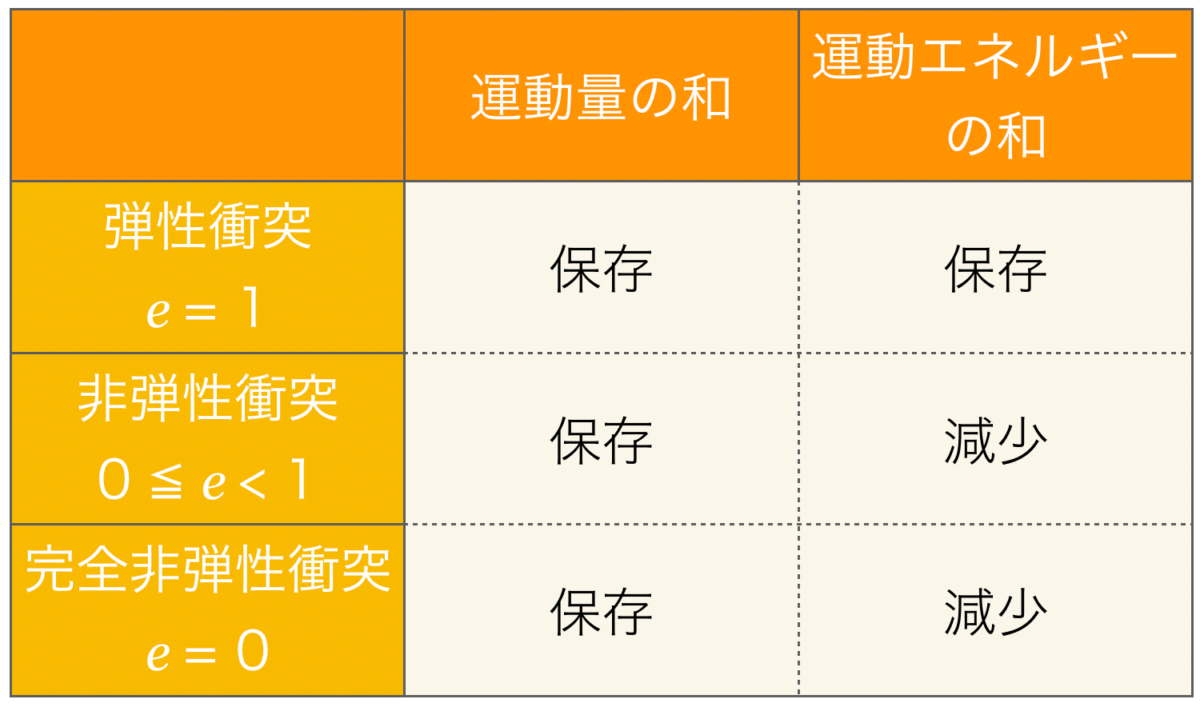
この表から，選択肢の②は正しいということになります。つまり，答えは②です。
答えは②ですが，他の選択肢にも重要な概念が含まれているので見てみましょう。
4. 運動エネルギーと仕事，運動量と力積
運動エネルギーと運動量は似ている点があるので，区別をしっかりとつけておくことが大切です。
選択肢の③は力を受けて速度が変化したときの話です。物体に力を加えると，運動エネルギーも運動量も変化をする可能性がありますが，その変化量はそれぞれ別の物理量で表すことができます。
文章で書くとこうなります。
物体の「運動エネルギーの変化」は，物体にされた「仕事」に等しい
物体の「運動量の変化」は，物体に与えた「力積」に等しい
これらの区別はとても重要なので覚えておく必要がありますが，最初にまとめたスカラーとベクトルの関係からも分かりますね。「運動エネルギー」と「仕事」はスカラー，「運動量」と「力積」はベクトルなのです。
何れにしても，③の選択肢は間違っています。
ここで，一点だけ確認をしておきます。
1.「速度が変化」したとき，運動エネルギーは変化していますか？
2.「速度が変化」したとき，運動量は変化していますか？
「速度が変化」したとき，運動エネルギーも運動量も変化している可能性が高いのですが，「運動量」は確実に変化していて，「運動エネルギー」は変化していない可能性があります。
これは「速度」がベクトルであることによって，違いが出てくるのです。「速度の変化」というと，「速度の大きさ（速さ）」は変わらずに「速度の向き」だけが変わる，という状況もあり得るのです。この場合，「運動量」はベクトルなので，向きだけが変わったとしても「運動量」は変化しています。ところが，運動エネルギーはスカラーなので，向きは関係がありません。大きさが変わらないと運動エネルギーは変わったことにはならないのです。
5. 等速円運動は「速度が一定の円運動」ではない！
最後の選択肢④について考えます。この選択肢が答えだとした人が結構いたようです。この選択肢のポイントは「等速円運動」の「等速」の部分についてです。等速円運動を簡単に描くとこんな感じです。
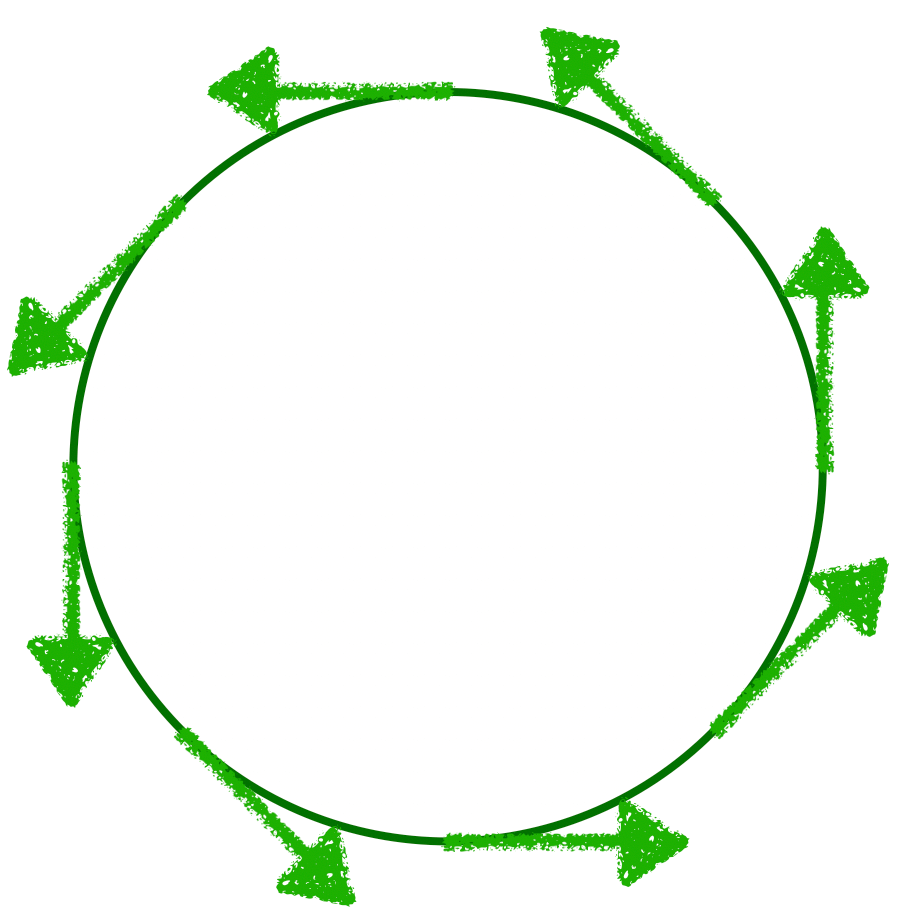
矢印は速度を表しています。つまり，速さは一定ですが，向きは常に変化しているのが「等速円運動」です。この「等速円運動」の「等速」は速度が一定なのではなく，「速さ」が一定なのです。ということは，等速円運動では「運動エネルギー」は常に一定ですが，「運動量」は常に変化しているということになります。なので，選択肢④は間違いで，答えは②ということになります。
