この問題の4つのポイント
- 点電荷がつくる電場の向きを理解しよう
- 点電荷がつくる電場の大きさと電位の式を混同しない
- 電場はベクトルなので,しっかりと図を描こう
- 一直線上の問題では,qもQもとりあえず正として考える方法もある
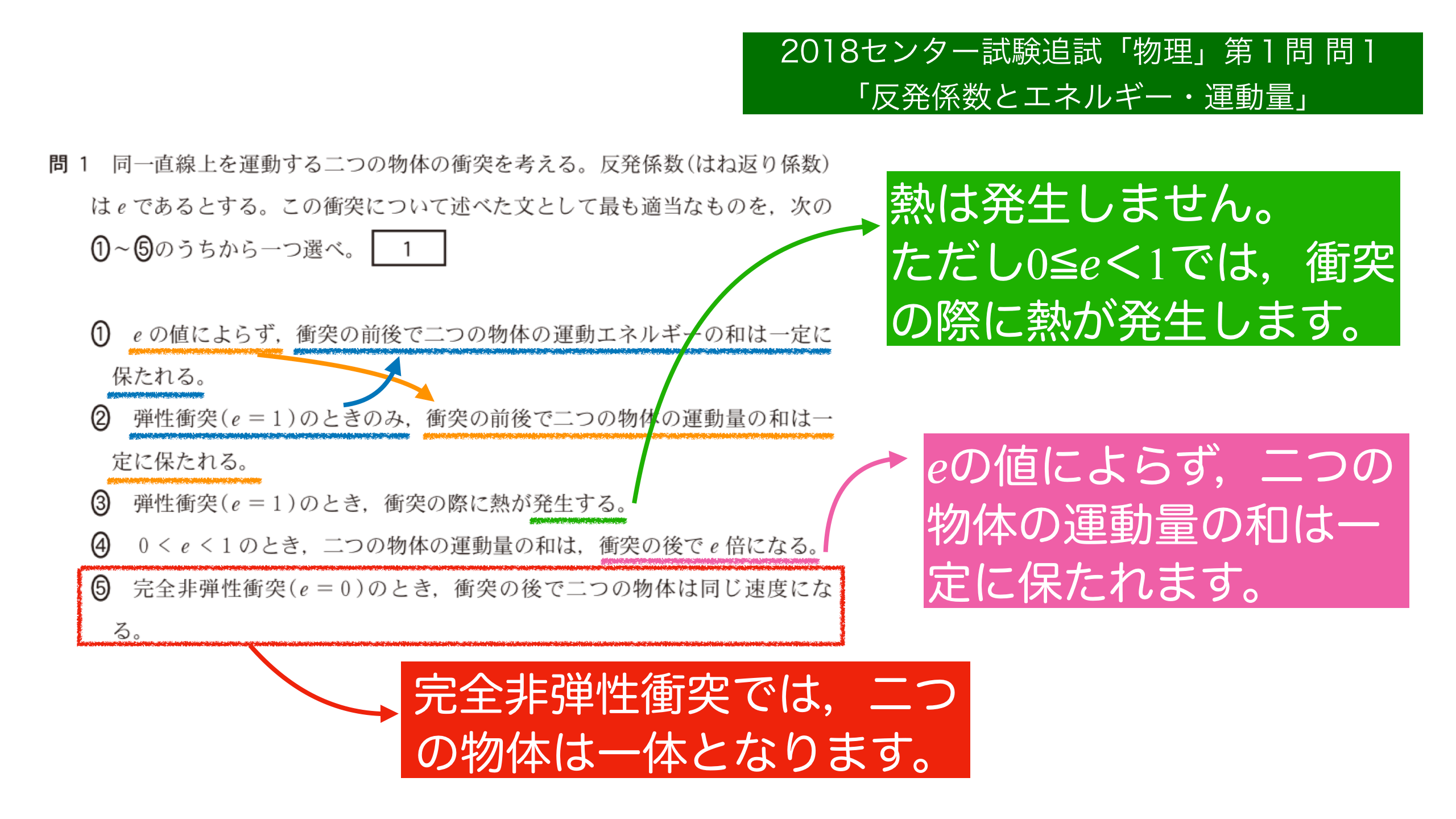
1. 点電荷がつくる電場の向きを理解しよう
電場(電界)は向きを持つベクトルです。まずは向きについて考えます。
点電荷がつくる電場の向きは,その点電荷が正か負かで変わります。電場の向きは分かってしまうと簡単なことですが,うまくポイントが掴めないと,「何を言っているのかさっぱり分からない」ということになってしまいます。
点電荷がつくる電場の向きについて,簡単にまとめておきましょう。正の電荷からは出て行く向きに,負の電荷は入ってくる向きに電場ができます。ここまでは問題がないと思います。
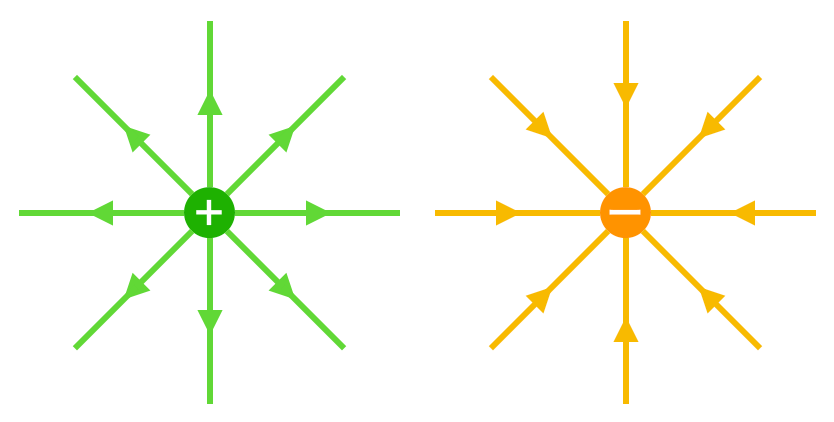
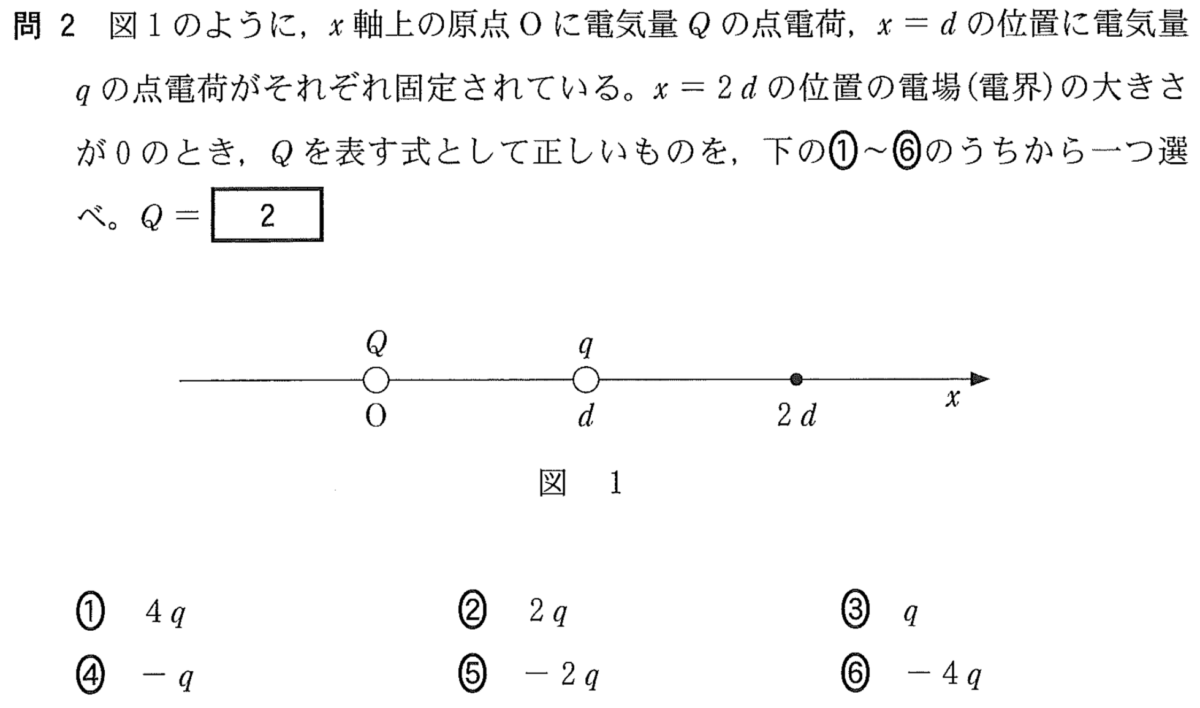
ところが,この点電荷から離れた地点の電場の向きとなると,分からなくなる人が必ずいます。下の図で,点Oにできる電場の向きはどちらになるでしょうか。
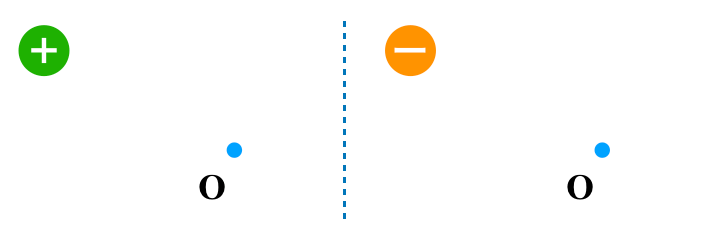
あくまでも点Oにできる電場の向きなのですが,いろいろなタイプの矢印を描く人がいます。点Oにできる電場の向きはそれぞれこのようになります。
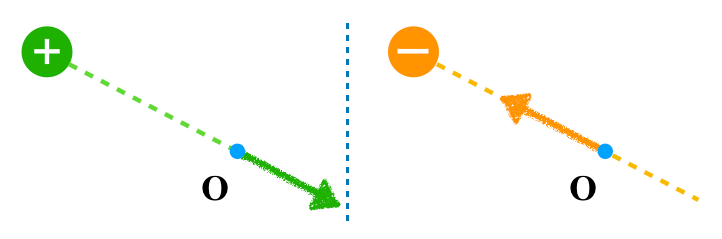
いかがでしょうか。この向きをベースにこの問題を考えます。
2. 点電荷がつくる電場の大きさと電位の式を混同しない
次に電場の大きさ(強さ)を考えます。ただ,この点電荷に関する式がたくさんあって,しかもよく似ているので,どうしても混同してしまいます。しっかりとまとめておきましょう。

とても似ていますね。電位の式については無限遠を基準とした時の式になります。この問題で使う点電荷がつくる電場の大きさの分母はrの2乗です。
3. 電場はベクトルなので,しっかりと図を描こう
電場に限らず,速度,加速度,力などのベクトルを考える問題では,向きがとても重要になるので図をしっかりと描きましょう。
まずは,![]() の位置にある電気量
の位置にある電気量![]() の電荷が
の電荷が![]() の位置につくる電場を考えます。実はこの電気量
の位置につくる電場を考えます。実はこの電気量![]() が正なのか,負なのか分かりません。正負が分からなければ,電場の向きが分からなので図が描けません。そのままだと問題が解けないのですが,そもそも問題に電気量の正負が書かれていないということは,正負が分からなくても問題が解けるということです。
が正なのか,負なのか分かりません。正負が分からなければ,電場の向きが分からなので図が描けません。そのままだと問題が解けないのですが,そもそも問題に電気量の正負が書かれていないということは,正負が分からなくても問題が解けるということです。
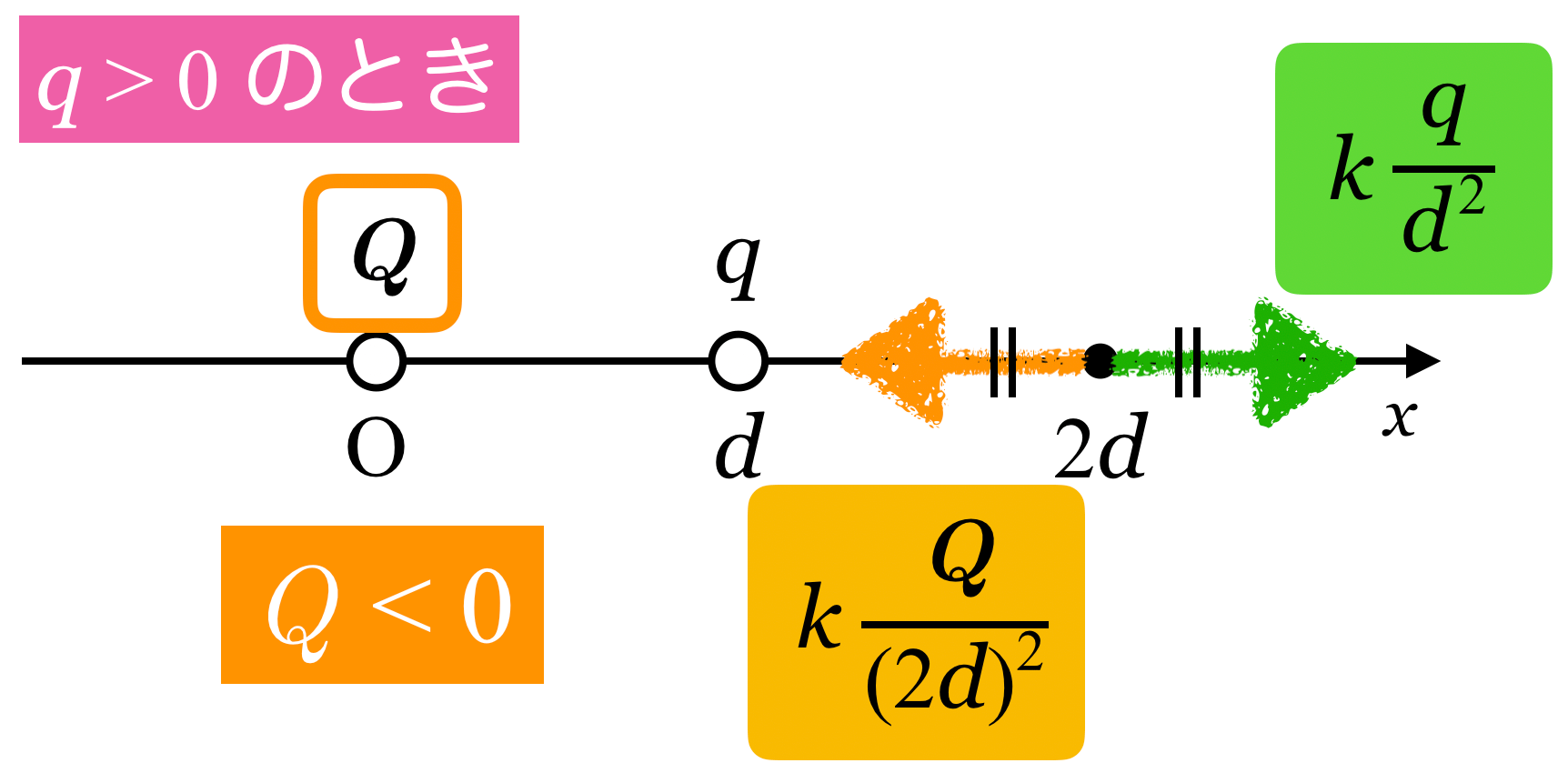
そこで,とりあえず図を描くために電気量![]() を正として考えてみましょう。クーロンの法則の比例定数を
を正として考えてみましょう。クーロンの法則の比例定数を![]() として,電場の向きと大きさを考えるとこうなります。
として,電場の向きと大きさを考えるとこうなります。
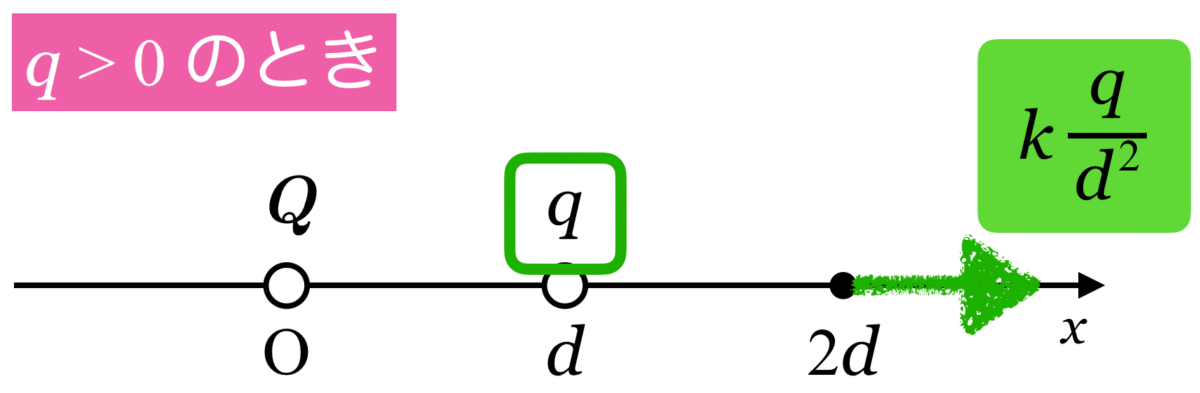
問題文には「![]() の位置の電場(電界)の大きさが0」とあります。ということは,原点にある電気量
の位置の電場(電界)の大きさが0」とあります。ということは,原点にある電気量![]() の電荷が
の電荷が![]() につくる電場の向きは図の左向き,つまり
につくる電場の向きは図の左向き,つまり![]() 軸の負の向きです。なので,電気量
軸の負の向きです。なので,電気量![]() の電荷は負でなければなりません。
の電荷は負でなければなりません。
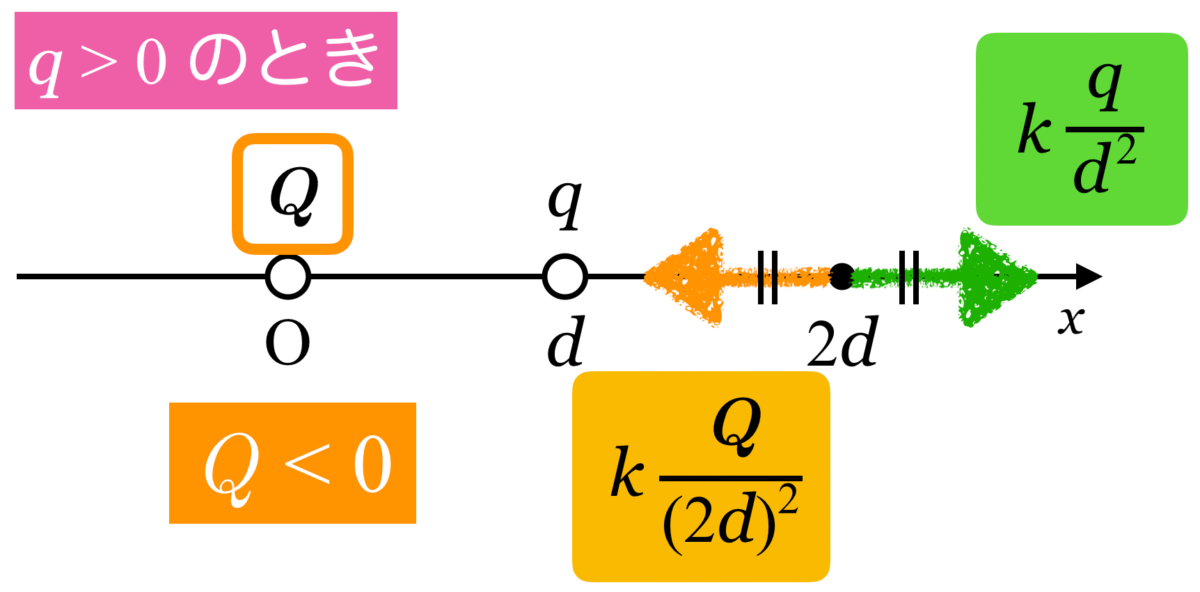
今電気量![]() を正とした結果,電気量
を正とした結果,電気量![]() は負となりました。もし,電気量
は負となりました。もし,電気量![]() を負の場合は電場の向きが逆になり,電気量
を負の場合は電場の向きが逆になり,電気量![]() がつくる電場の向きも逆になる必要があるので,正の電荷ということになります。
がつくる電場の向きも逆になる必要があるので,正の電荷ということになります。
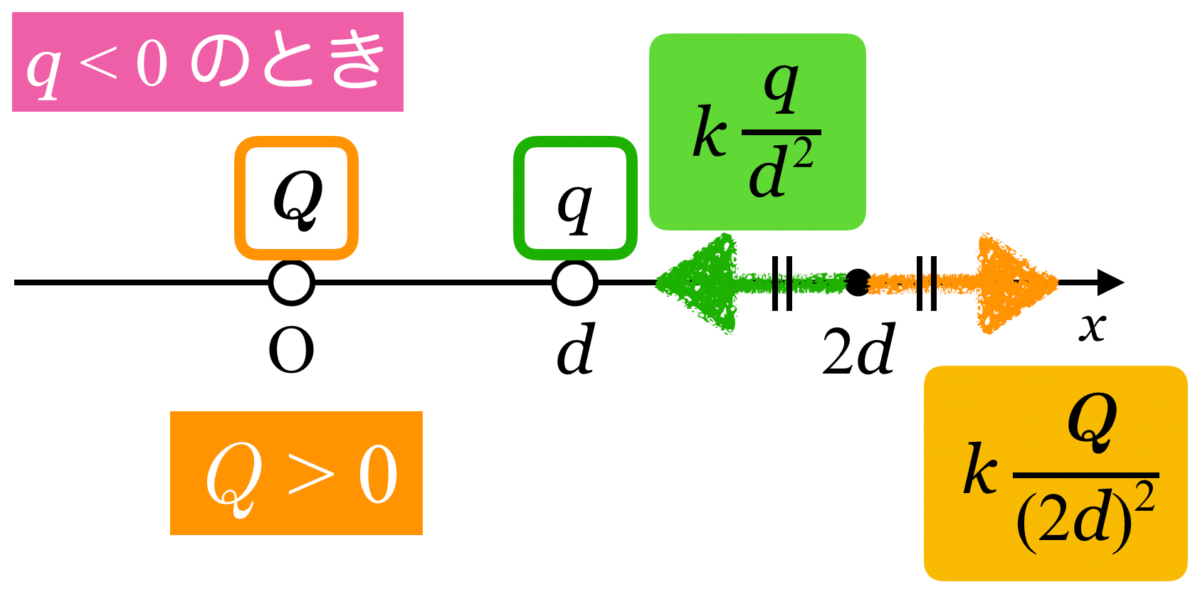
結果として,![]() と
と![]() の電荷の符号は必ず逆になります。選択肢の①から③は消えます。
の電荷の符号は必ず逆になります。選択肢の①から③は消えます。
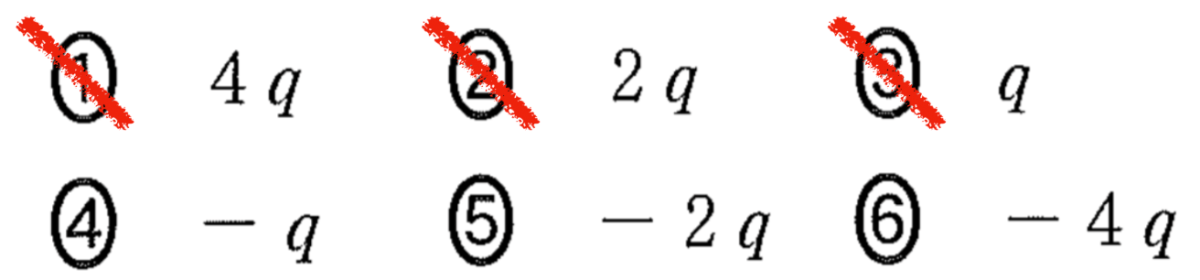
あとは計算をしましょう。![]() の位置の電場の大きさが0ということから,
の位置の電場の大きさが0ということから,![]() と
と![]() の電荷がつくる電場の大きさは同じになります。
の電荷がつくる電場の大きさは同じになります。
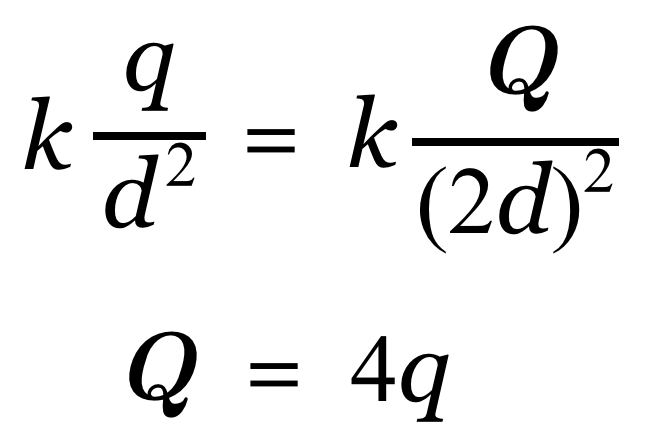
大きさは![]() となるので,符号の関係から答えは⑥
となるので,符号の関係から答えは⑥![]() になります。
になります。
4. 一直線上の問題では,qもQもとりあえず正として考える方法もある
この問題では2つの電荷と電場を考える点![]() の3つの点が全て一直線上(
の3つの点が全て一直線上(![]() 軸上)にあります。このような場合には,
軸上)にあります。このような場合には,![]() も
も![]() もどちらも正として考える方法があります。どちらも正とすると,電場の矢印の向きはどちらも右向きになります。
もどちらも正として考える方法があります。どちらも正とすると,電場の矢印の向きはどちらも右向きになります。
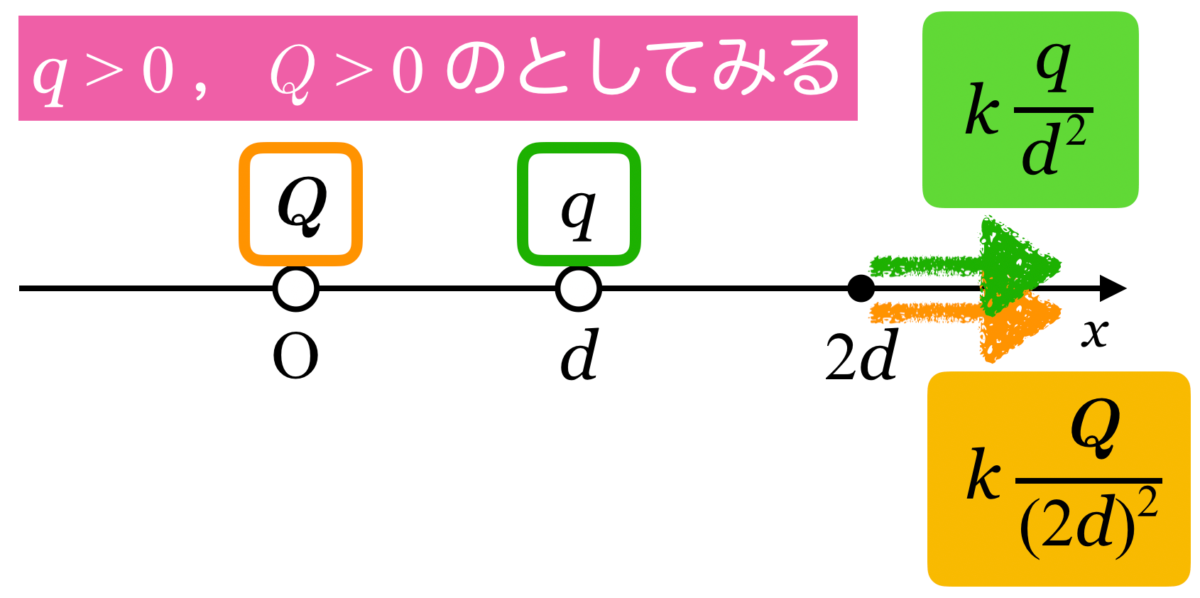
この2つの電場を合わせると0になることから,
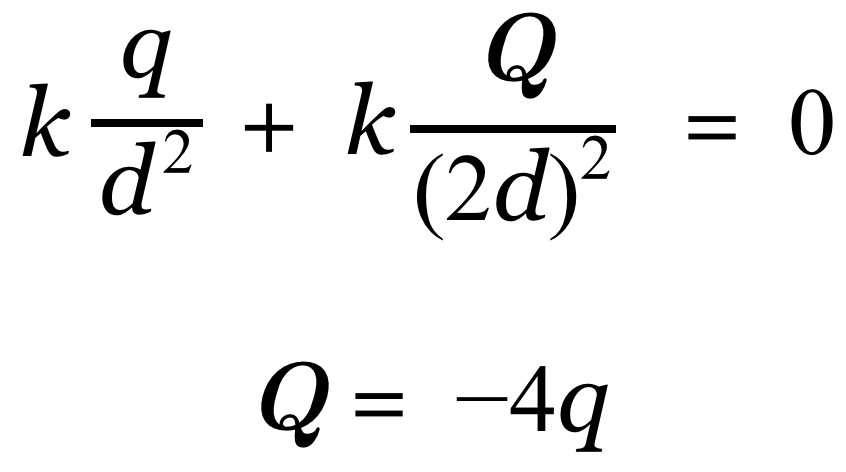
となり,この方法だと符号も含めて計算結果が出てきます。便利な方法ではありますが,2つの電荷と電場を考える点の3点が一直線上にある時しか使えません。一直線上にないときは,向きと大きさを別々に考えましょう。