センター2019物理第３問Ａ「薄膜干渉と光の屈折」

スポンサーリンク

薄膜干渉を基本から考える

物理が苦手な文子
この問題の図はなんとなく見たことがあるわ。
物理が得意な秀樹
薄膜干渉の図だね。
物理が苦手な文子
薄膜干渉ね。公式があるんだっけ？
物理が得意な秀樹
薄膜干渉の干渉条件の式を暗記している人もいるかもしれないけど，この問題では暗記していることがあんまり使えないかもね。
物理が苦手な文子
「あんまり使えない」ってどういうこと？
物理が得意な秀樹
もちろん干渉条件は覚えていてもいいけど，もっと大切なのはこの干渉条件を自分で導き出せるようになることなんだ。
物理が苦手な文子
自分で導き出すのは難しそう。
物理が得意な秀樹
難しいかもしれないけど，薄膜干渉の問題では導き出された干渉条件を使うのではなく，干渉条件を導き出す過程で使う考え方を問題にすることが多いんだよ。この問題もそうだね，
物理が苦手な文子
それじゃあ，何をすればいいの？
物理が得意な秀樹
最初の問題は屈折率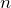nを求める問題だね。
物理が苦手な文子
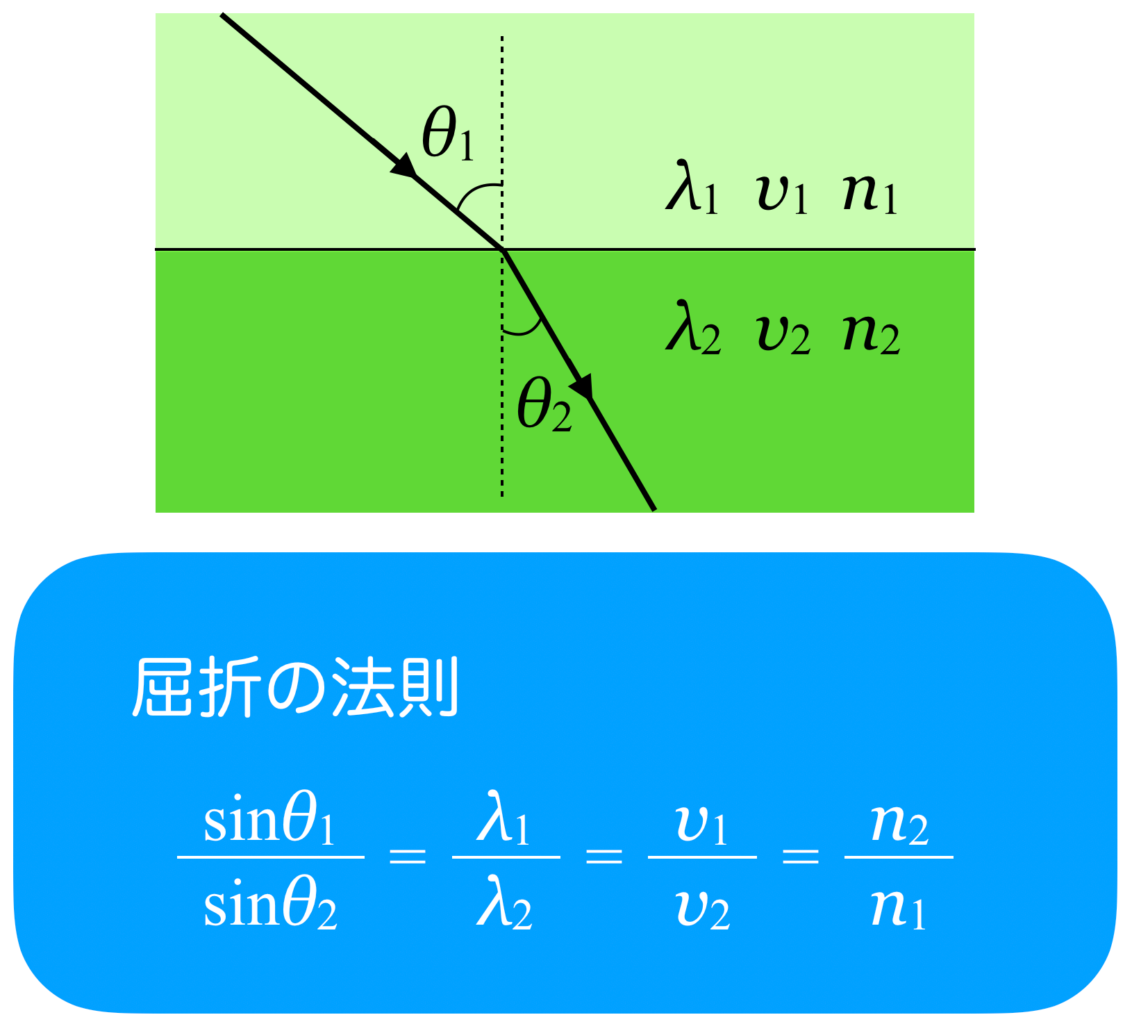
屈折率を求めるといことは，屈折の法則を使うのね。
物理が得意な秀樹
その発想はとてもいい。ただ，屈折率を線分の長さを用いて表す問題なんだよ。屈折の法則には「線分の長さ」っていうのは出てこなかったね。
物理が苦手な文子
そうね。屈折の法則って，角度とか，速さとか，波長の比だったわね。あっ，波長は長さだから，波長が関係ある？

物理が得意な秀樹
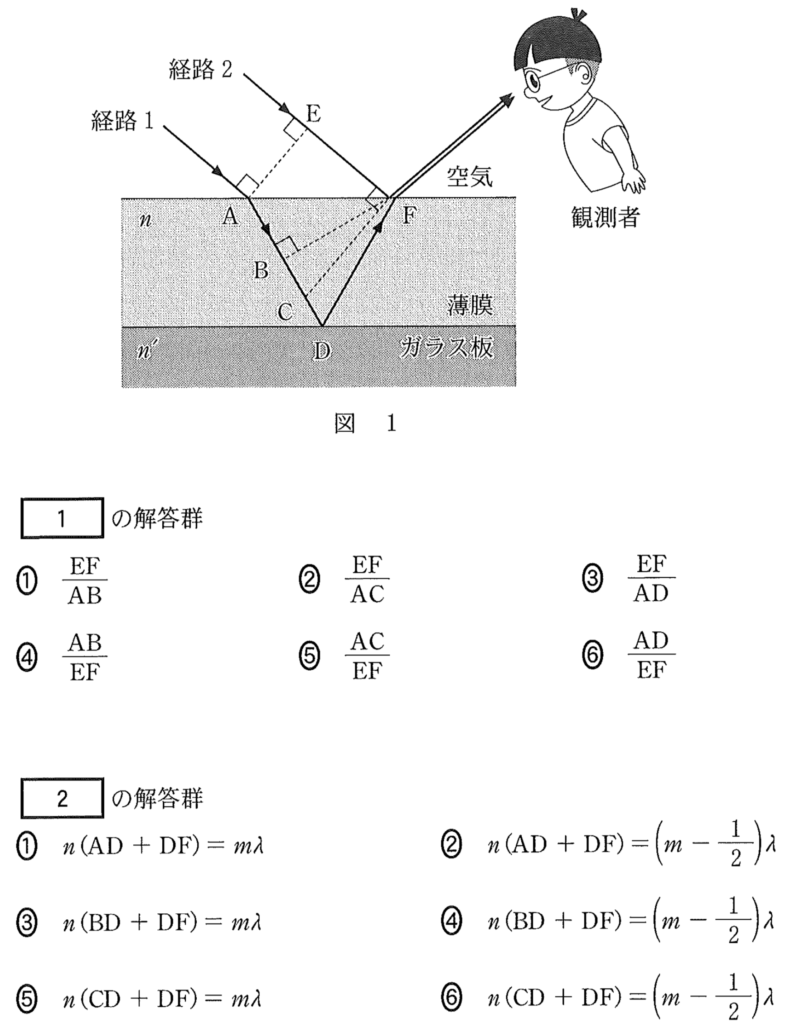
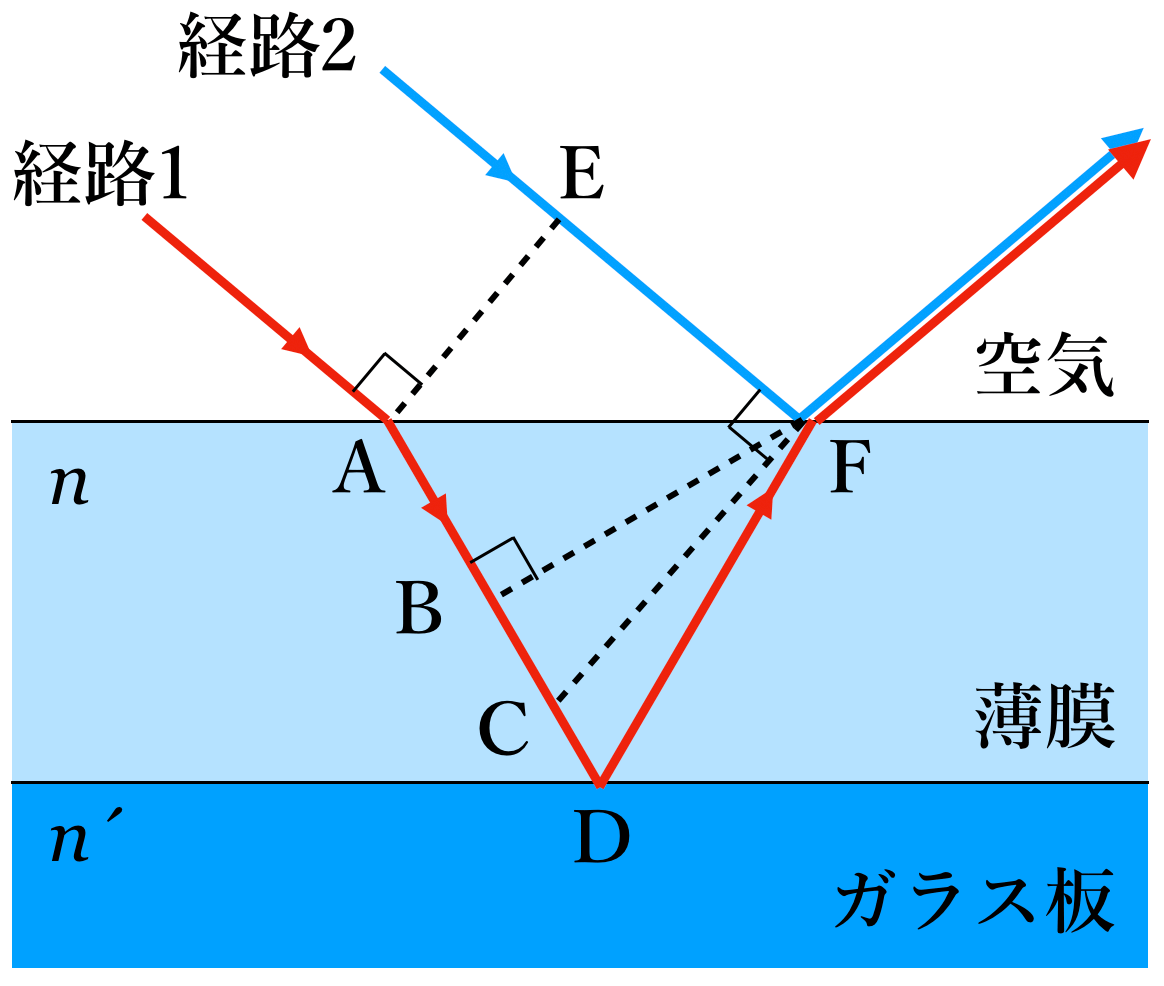
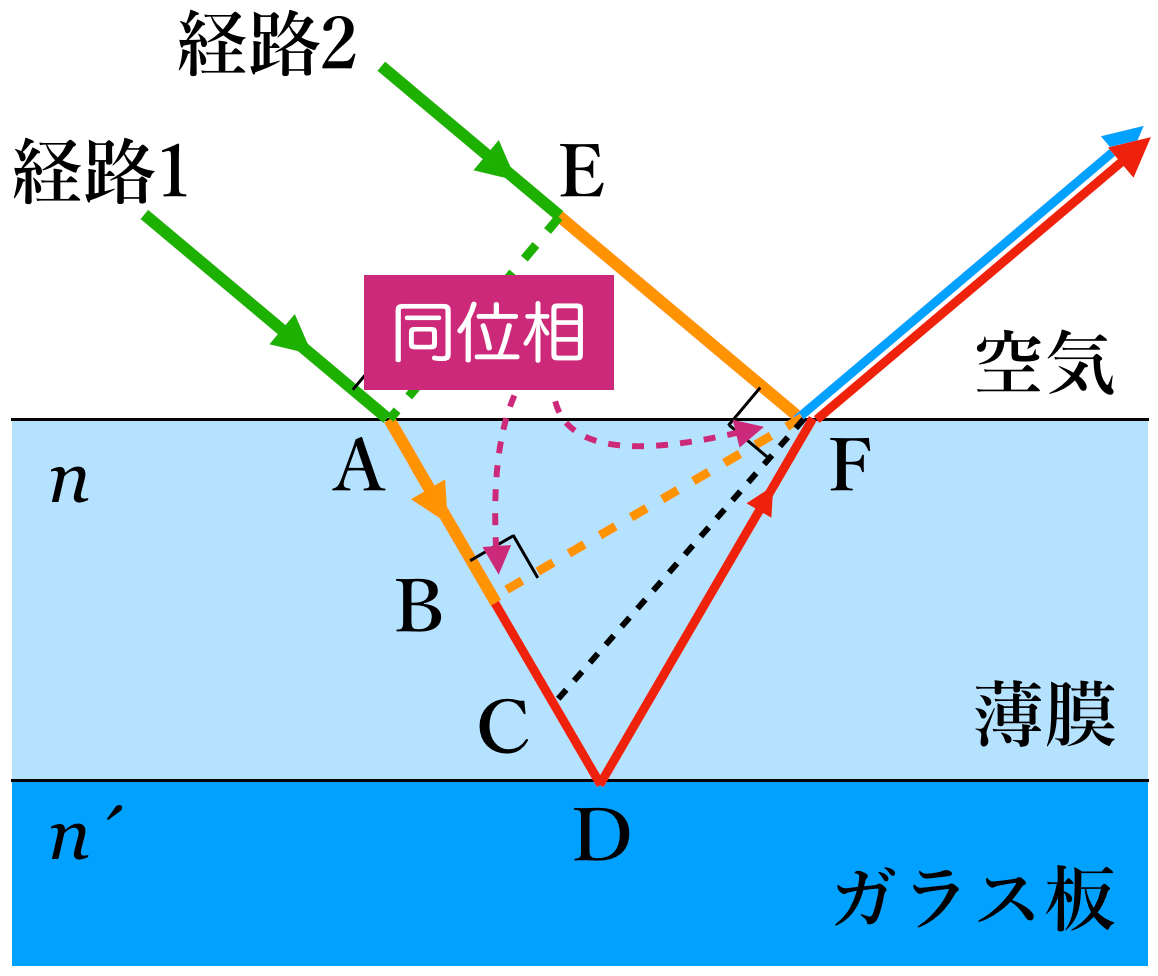
そうだね。波長は関係あるけどいろいろと大切なことがあるので，順番に説明していくよ。まず，２つの経路に色を付けてみるよ。この赤い経路１と青い経路２を通った２つの光が干渉するんだね。

物理が苦手な文子
見やすいわね。

２つの経路で同位相の位置を確認する

物理が得意な秀樹
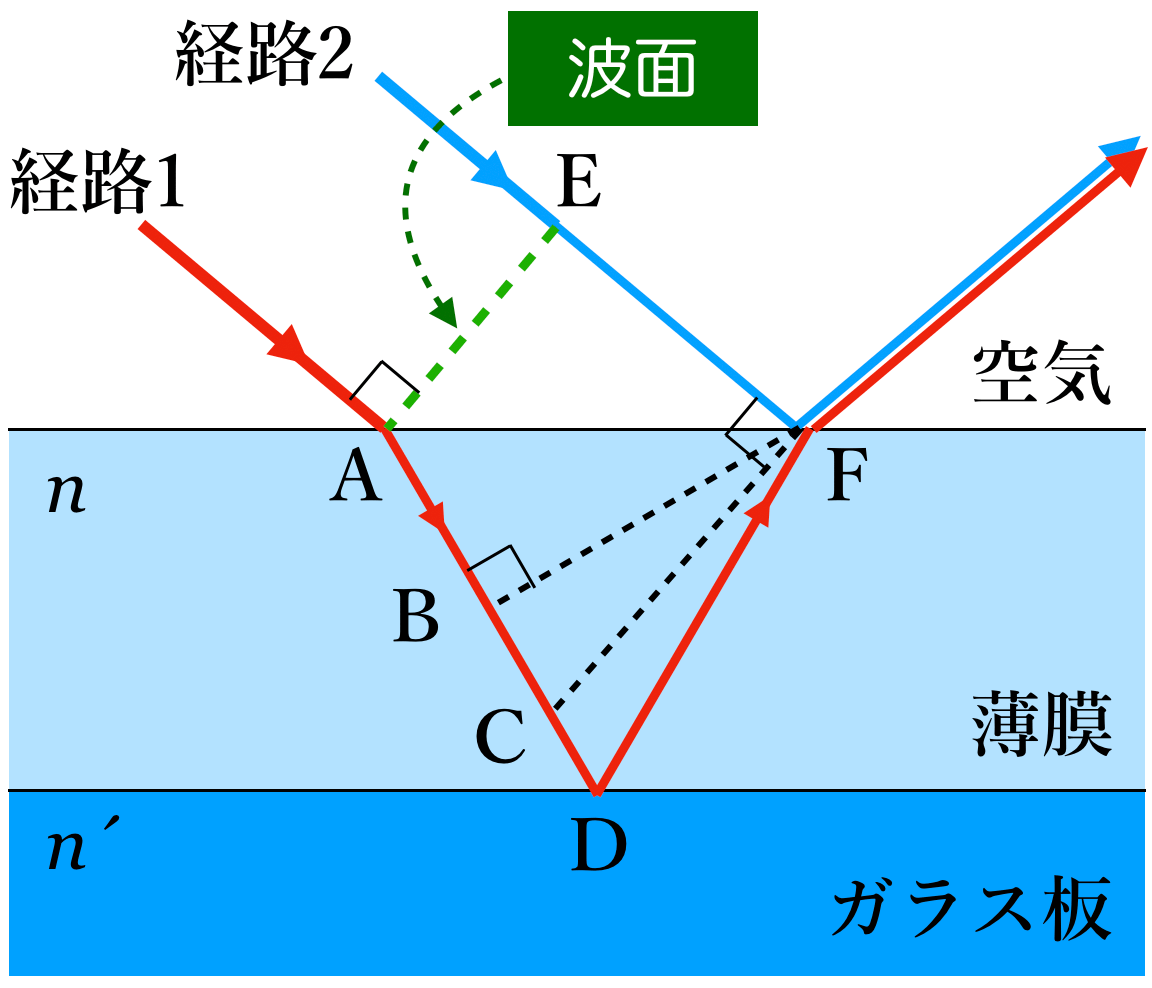
少し見やすくなったでしょ。図の左上から来る２つの光に共通の垂線を引くと，その線が波面になるんだ。
物理が苦手な文子
波面って何？
物理が得意な秀樹
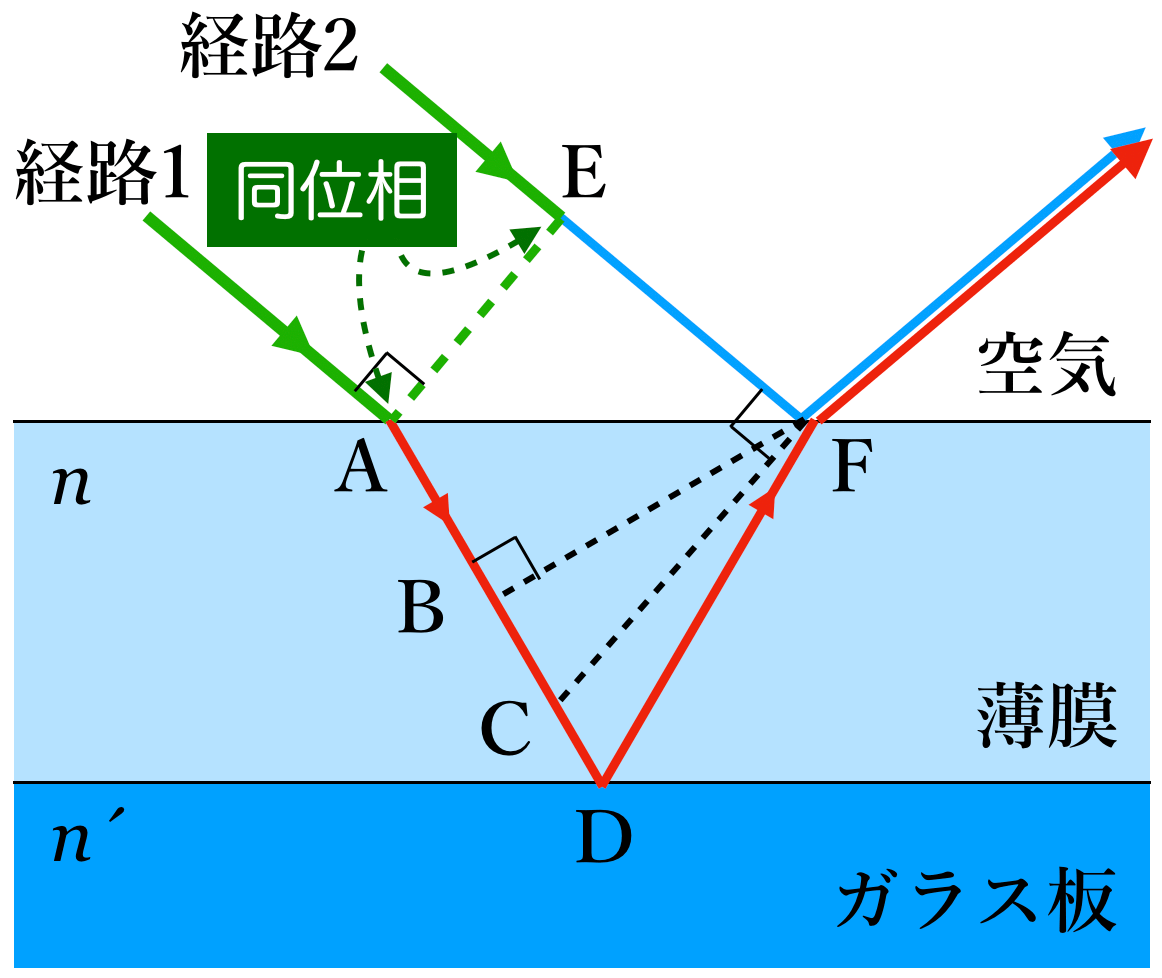
左上から来る光の位相が同じ点を結んだ線だね。図のAとEは同じ位相ということなんだ。例えばAもEも山ということだ。
物理が苦手な文子
そうなの。
物理が得意な秀樹
同様に，経路１の光は屈折をして薄膜中に入っていくけど，これも垂線を引くと波面になるので，図のBとFは同位相なんだ。
物理が苦手な文子
AとEは同位相で，BとFも同位相ということなのね。
物理が得意な秀樹
そう。ここで，問題を見てみると屈折率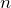nを求めるんだけど，すべての選択肢の中にEFという長さが入っているよね。
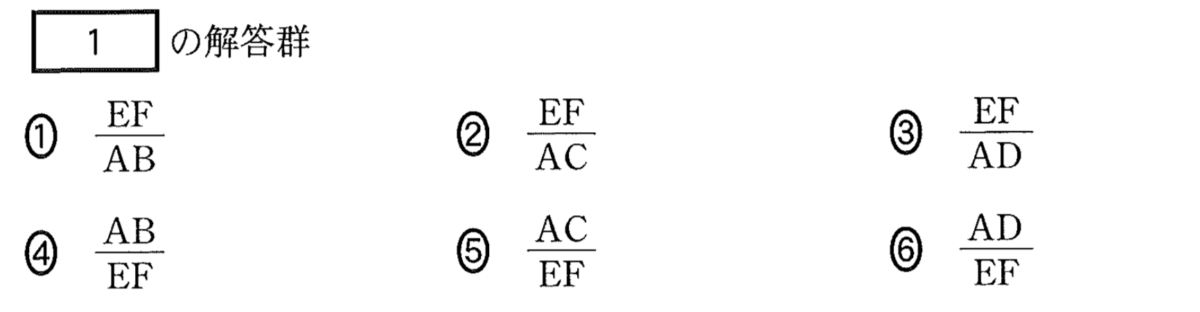
物理が苦手な文子
本当だ。そうね。

「光路長」を確認する

物理が得意な秀樹
図のAとEが同位相でBとFが同位相なので，図のEFの部分とABの部分はEFの方が長いけど光にとっては同じ長さなんだ。この光にとっての長さを「光路長」とか「光学距離」と言うよ。
物理が苦手な文子
聞いたことはあるわ。
物理が得意な秀樹
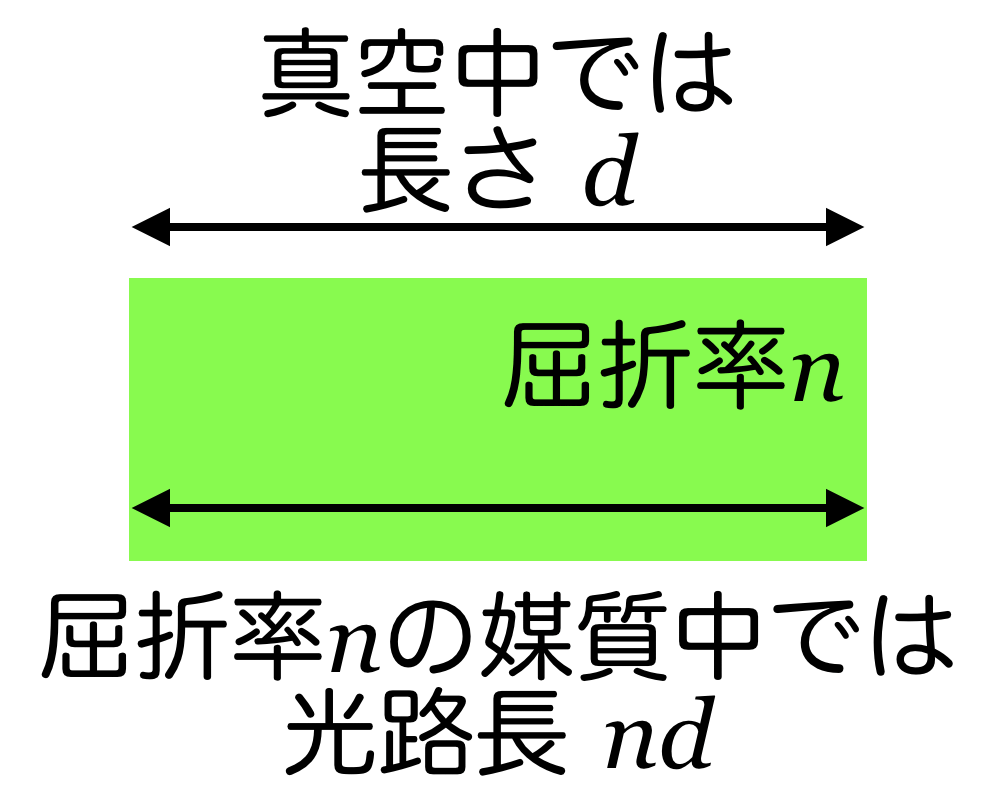
絶対屈折率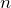nの媒質中を光が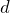dだけ進んだとき，光路長は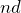ndと表せるんだ。
物理が苦手な文子
なるほど。
物理が得意な秀樹
ということは，EFは空気中なので光路長はそのままEFでいいけど，ABの光路長は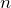nABと表せて，これらが等しいと考えるんだ。厳密には問題で与えられているのは空気に対する相対屈折率だけど，通常空気の屈折率は１と考えて良いので同じことだよ。
物理が苦手な文子
ということは，

    $$\rm{EF}=\it{n}\rm{AB}$$$$n=\frac{\rm{EF}}{\rm{AB}}$$


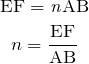
物理が得意な秀樹
そういうことだ。答えは①だ。次の空欄は強め合う条件を求めるんだね。

強め合う条件も基本に戻って考える

物理が苦手な文子
強め合う条件って，明るくなる条件と一緒？
物理が得意な秀樹
一緒だね。光の場合は「強め合う条件」を「明るくなる条件」とも言うんだ。この「薄膜干渉の干渉条件が使えればいいんだけど，残念ながらこの式を導き出す過程の考え方を使うんだ。
物理が苦手な文子
やっぱり使えないっていうことね。
物理が得意な秀樹
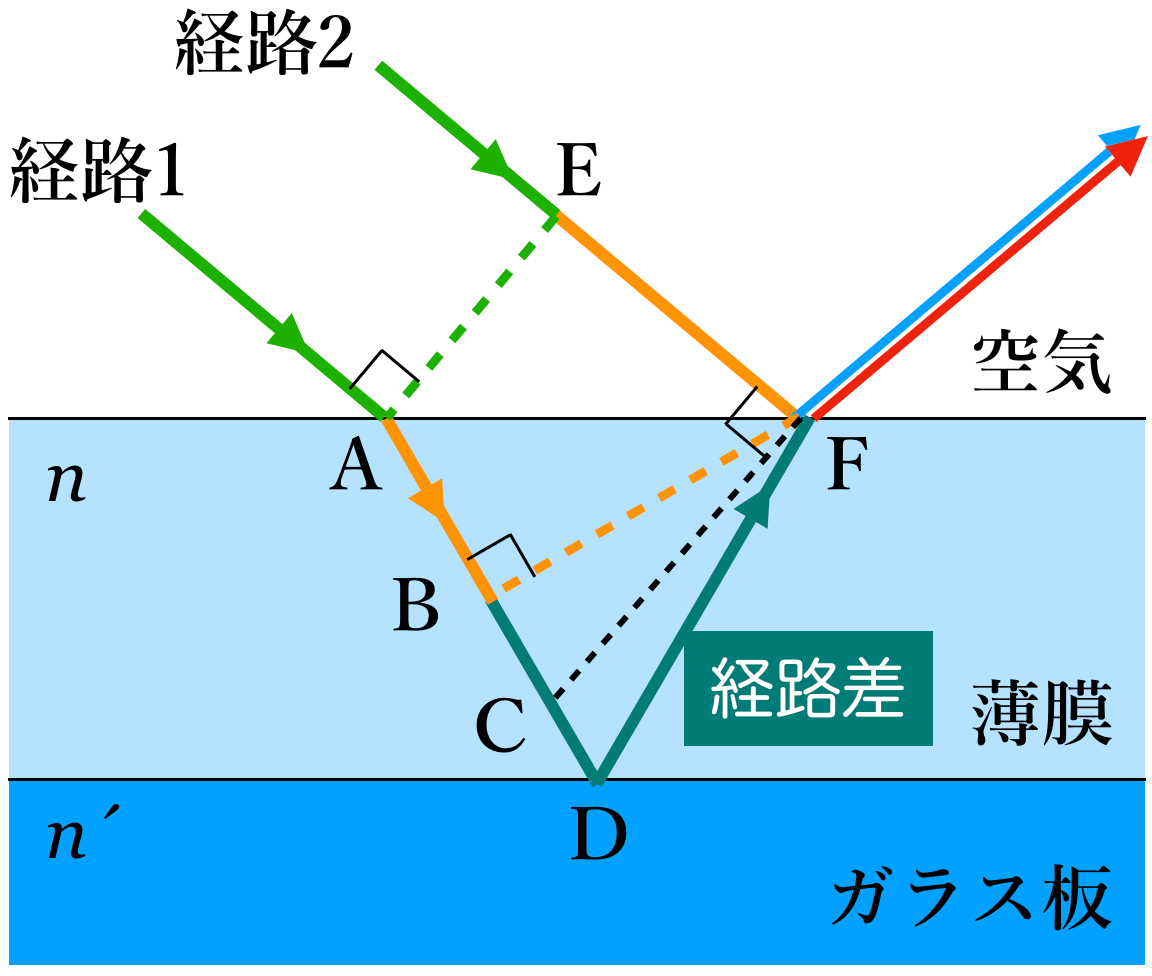
そうなんだよ。干渉条件を求めるには，一般にまずは経路差を求めるんだ。この問題の場合は，光にとってはBとFまでは位相が同じだということがわかっているので，経路差はこの図のように「BD+DF」になるんだ。
物理が苦手な文子
薄膜中を通る「経路１」の方が長いっていうことね。
物理が得意な秀樹
そうなんだ。だけど，薄膜は屈折率が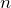nだから，光にとっての経路差（光路差）は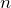n(BD+DF)になるんだ。
物理が苦手な文子
解答群で考えると，③か④ね。
物理が得意な秀樹
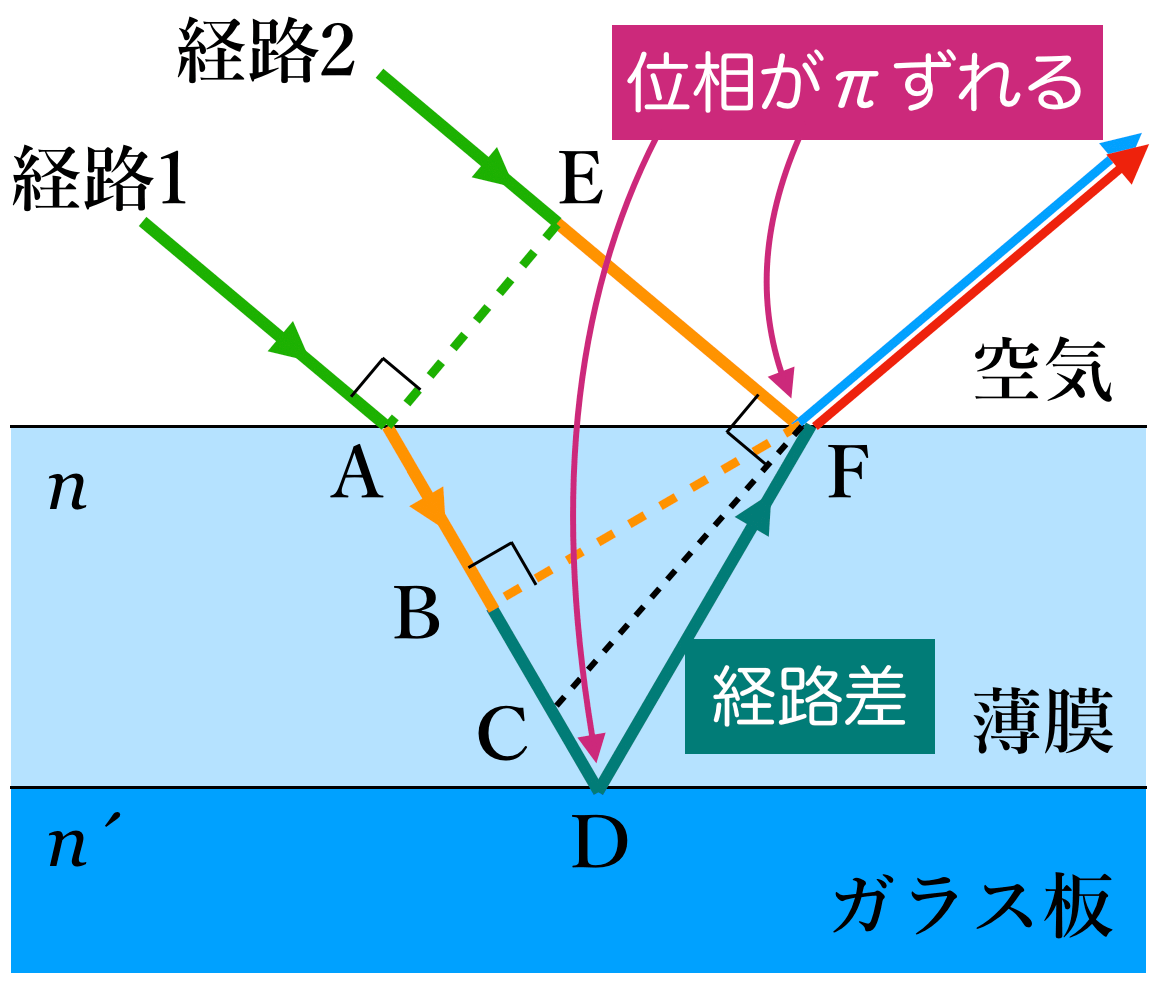
そうだね。さらに，反射による位相のずれを考える必要があるんだ。屈折率の小さい媒質から大きな媒質への境界で反射する場合は位相が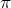\piだけずれるんだね。
物理が苦手な文子
経路１の光はDで位相が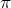\piずれて，経路２の光はFで位相が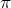\piずれるということね。
物理が得意な秀樹
そのとおりだ。経路１も経路２もどちらも位相が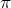\piずれるので，結局強め合う条件は通常の場合と変わらないんだね。
物理が苦手な文子
ということは，明るくなる条件は

    $$n(\rm{BD+DF})=\it{m\lambda}$$

物理が得意な秀樹
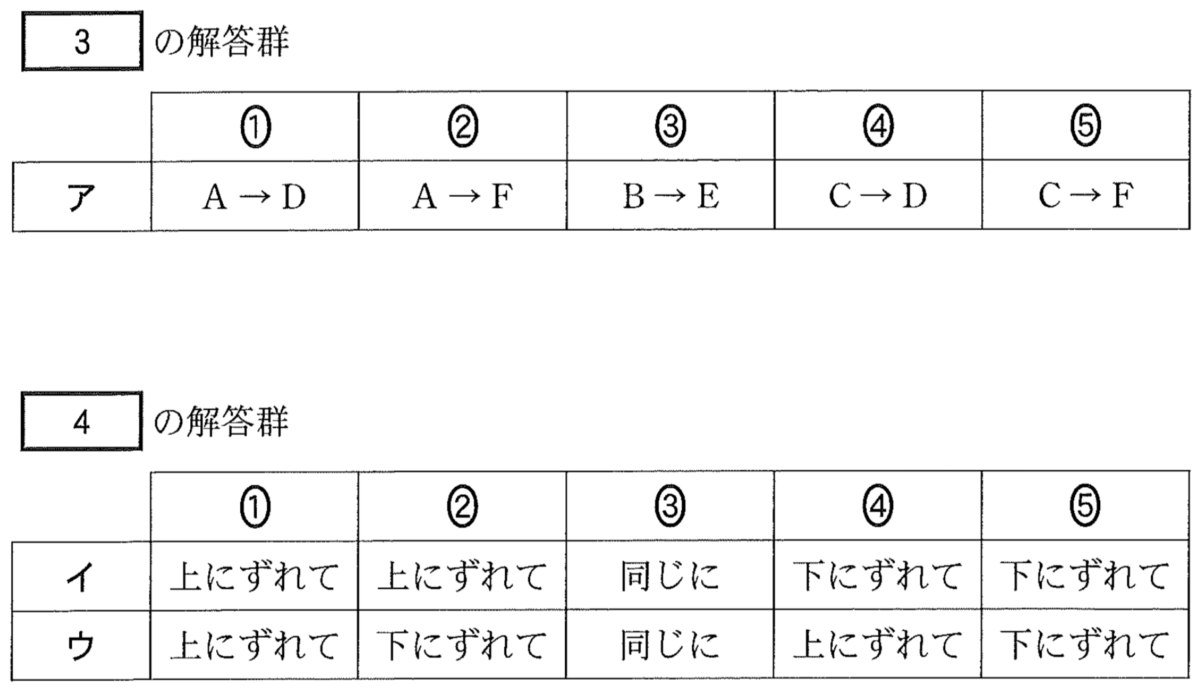
答えは③だね。問２にいこう。

屈折した光はどう見えるのか

物理が苦手な文子
問題がよく分からないわ。
物理が得意な秀樹
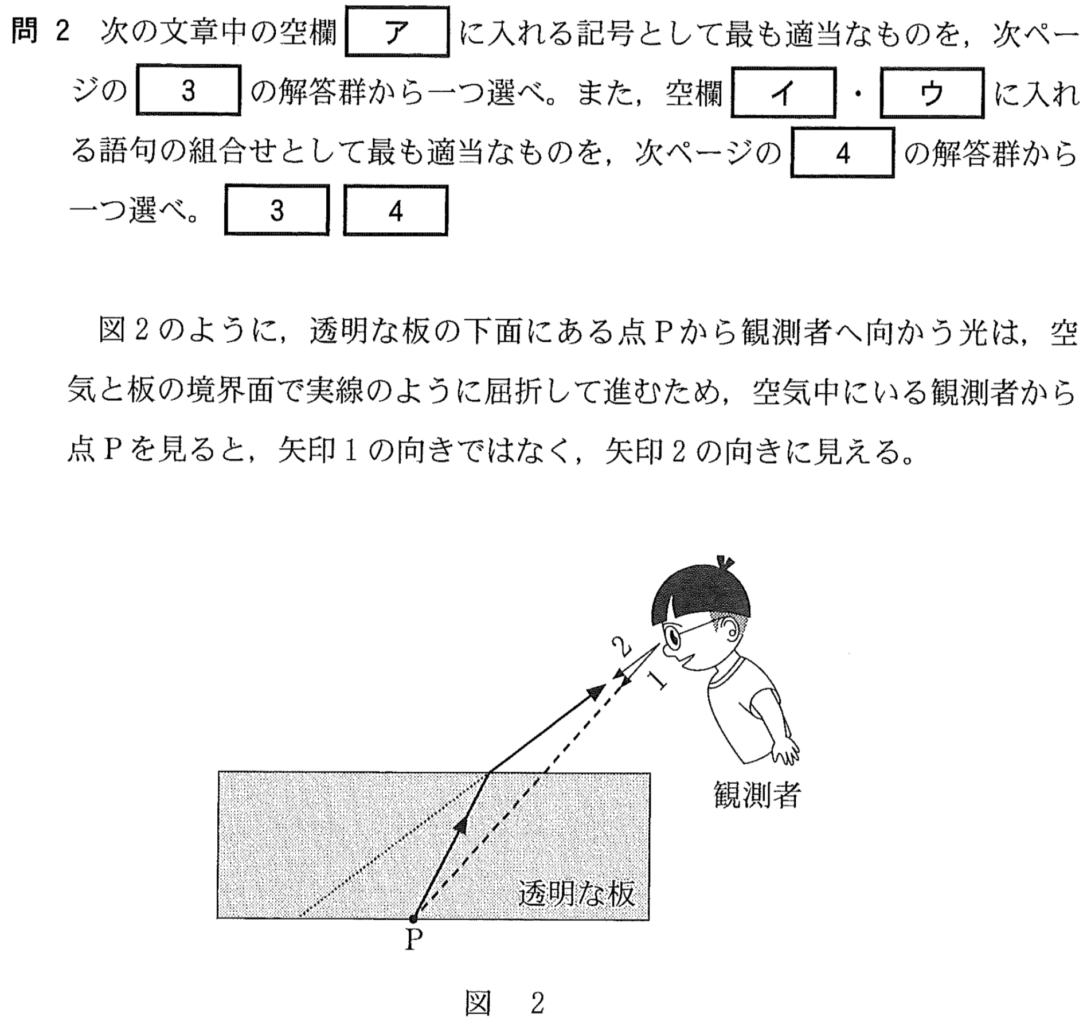
そうだね。光の屈折の問題なんだけど，どのように見えるかを考える問題になっているね。考え方については，図2のところの問題文で詳しく説明しているね。
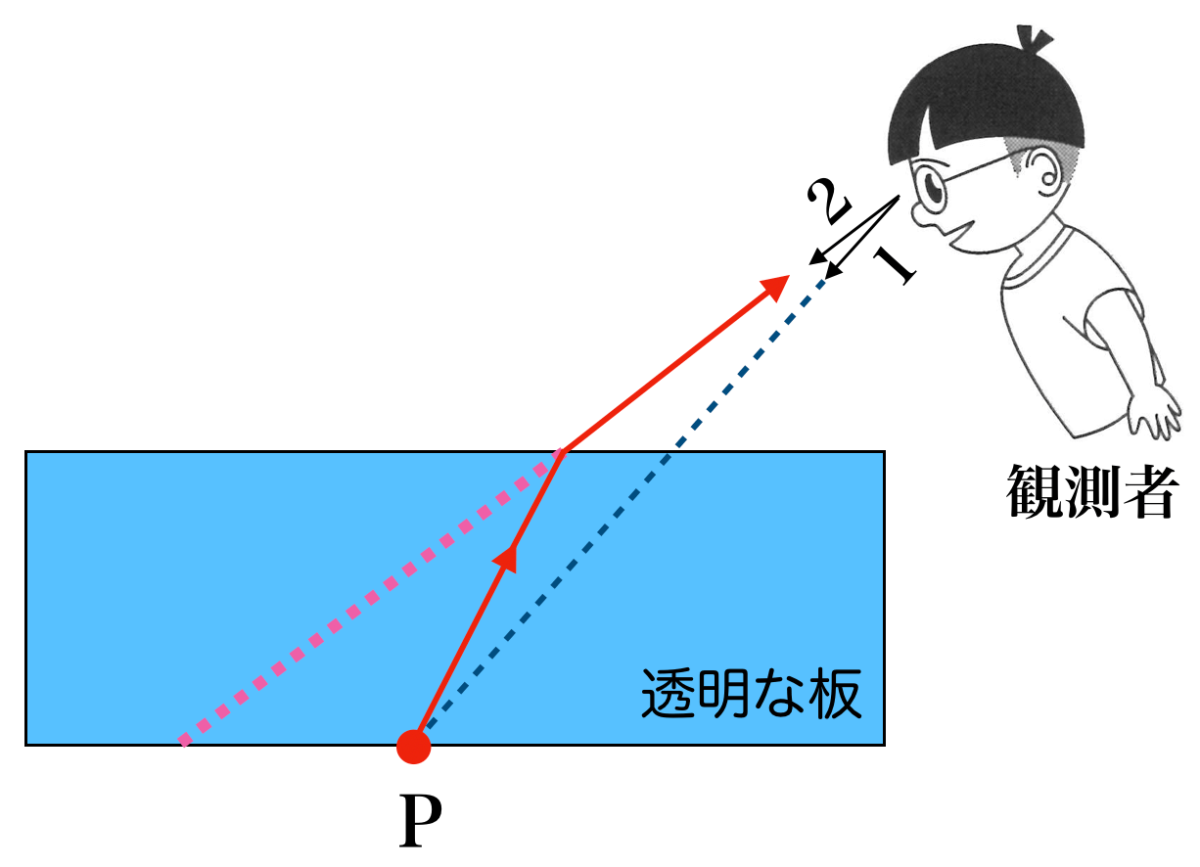
物理が得意な秀樹
点Pは観測者にとっては１の方向にあるんだけど，２の方向から光が来るので，点Pは２の方向に見えるんだ。
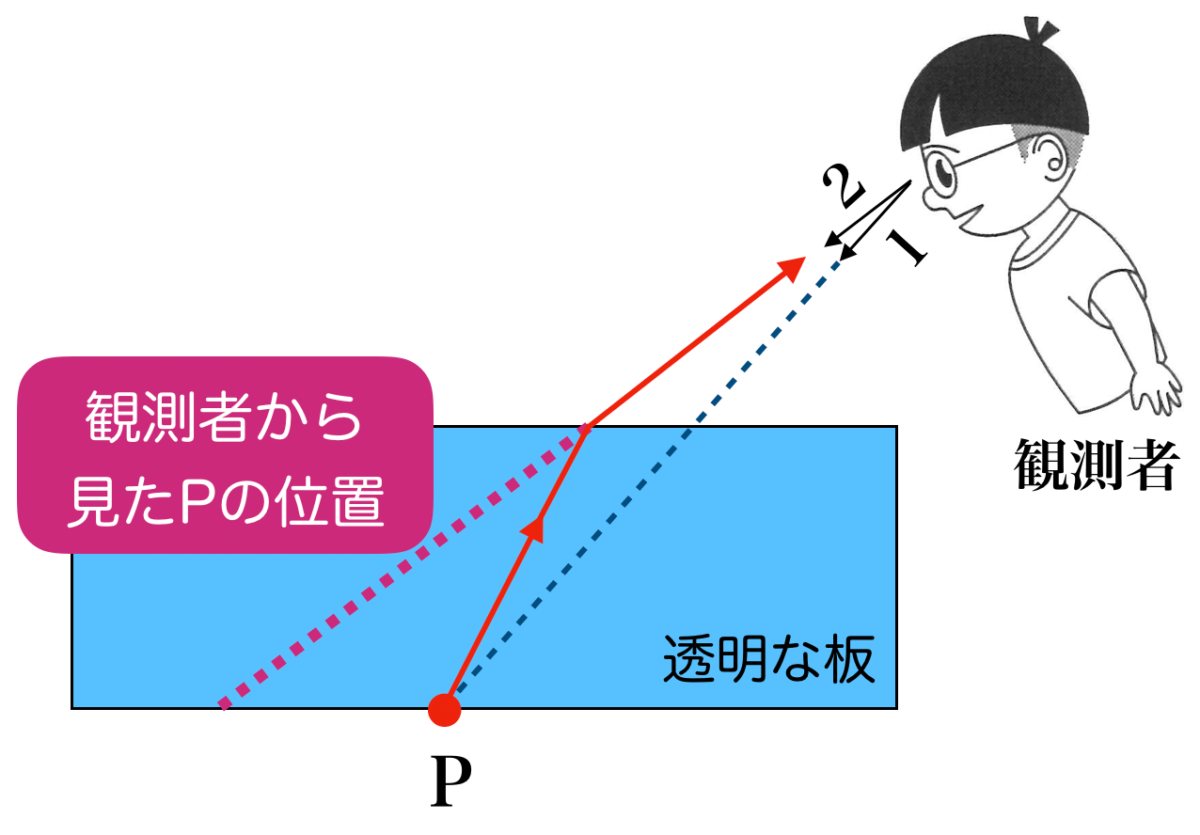
物理が苦手な文子
実際の場所とは違うところにあるように見えるのね。
物理が得意な秀樹
そうなんだよ。なので，この赤い矢印と同じ光の進行方向を選べば良いんだ。
物理が苦手な文子
でも線が入り組んでいて，ちょっと分かりにくいわ。

問題を回転させてみよう

物理が得意な秀樹
そういうときは，問題を回転させてみよう。
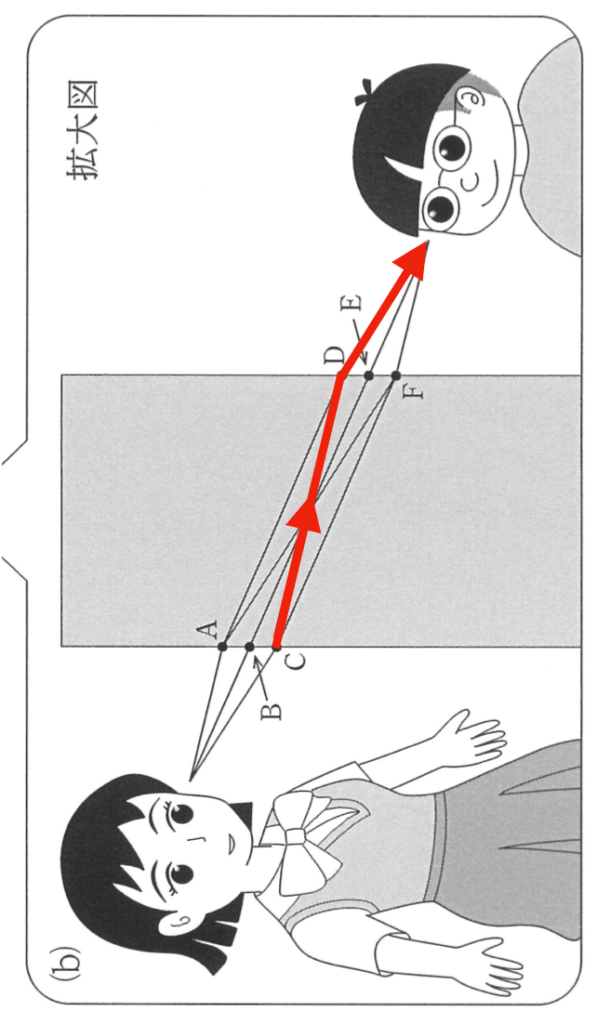
物理が苦手な文子
なるほど，CからDを通る光が同じ感じの経路なのね。
物理が得意な秀樹
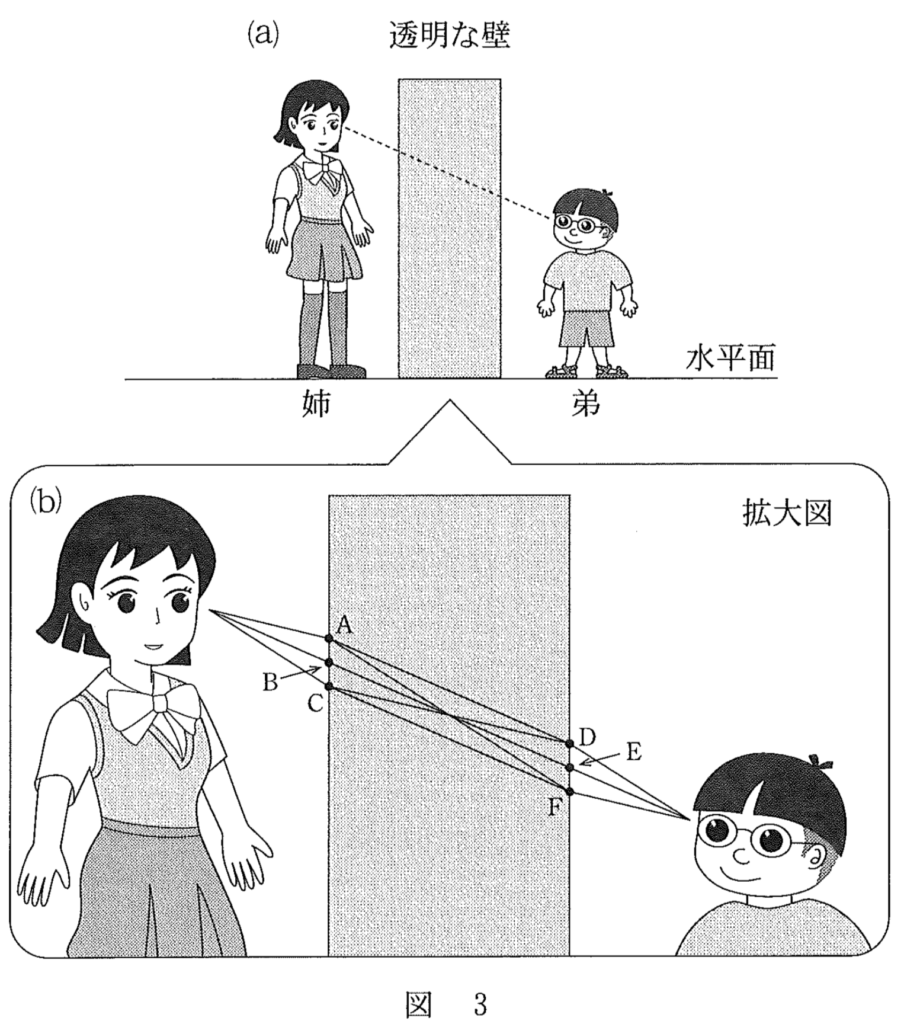
なので，光の経路は「C→D」の④だ。あとはお互いの目の位置がどっちにずれて見えるかだね。
物理が苦手な文子
これも最初の図がヒントなの？
物理が得意な秀樹
その通り，最初の図がヒントだ。
物理が苦手な文子
目に入る光線の延長線上に見えるのよね。だから，こういうこと？
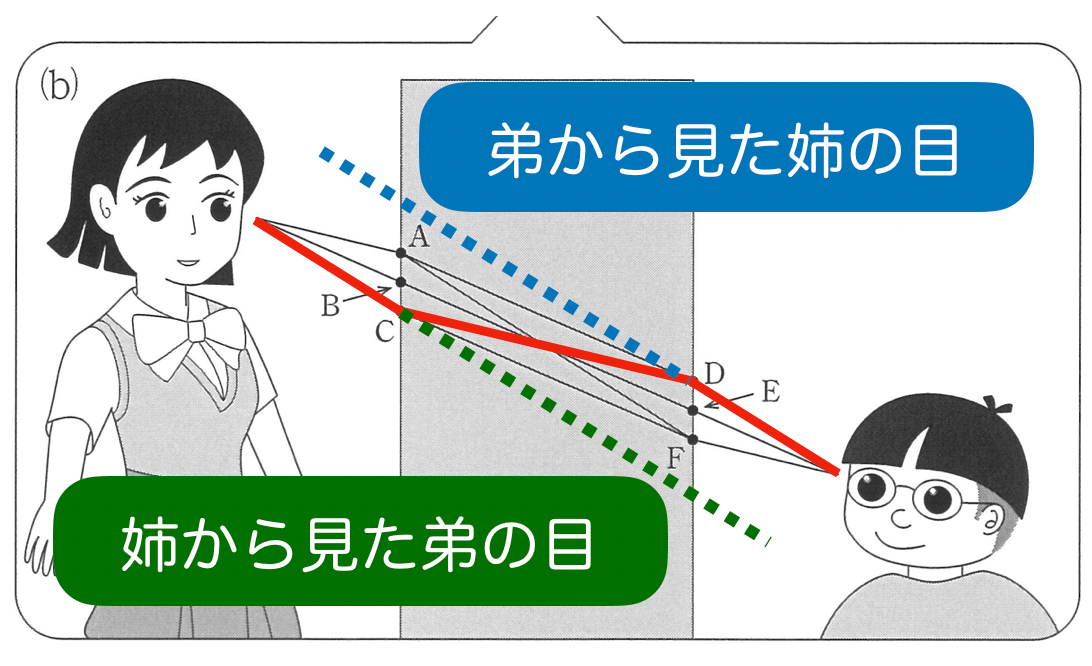
物理が得意な秀樹
そういうことだ。弟から見ると上にずれていて，姉から見ると下にずれているんだね。答えは②だ。
タイトルとURLをコピーしました