
三角関数のグラフを確認する
物理が苦手な文子
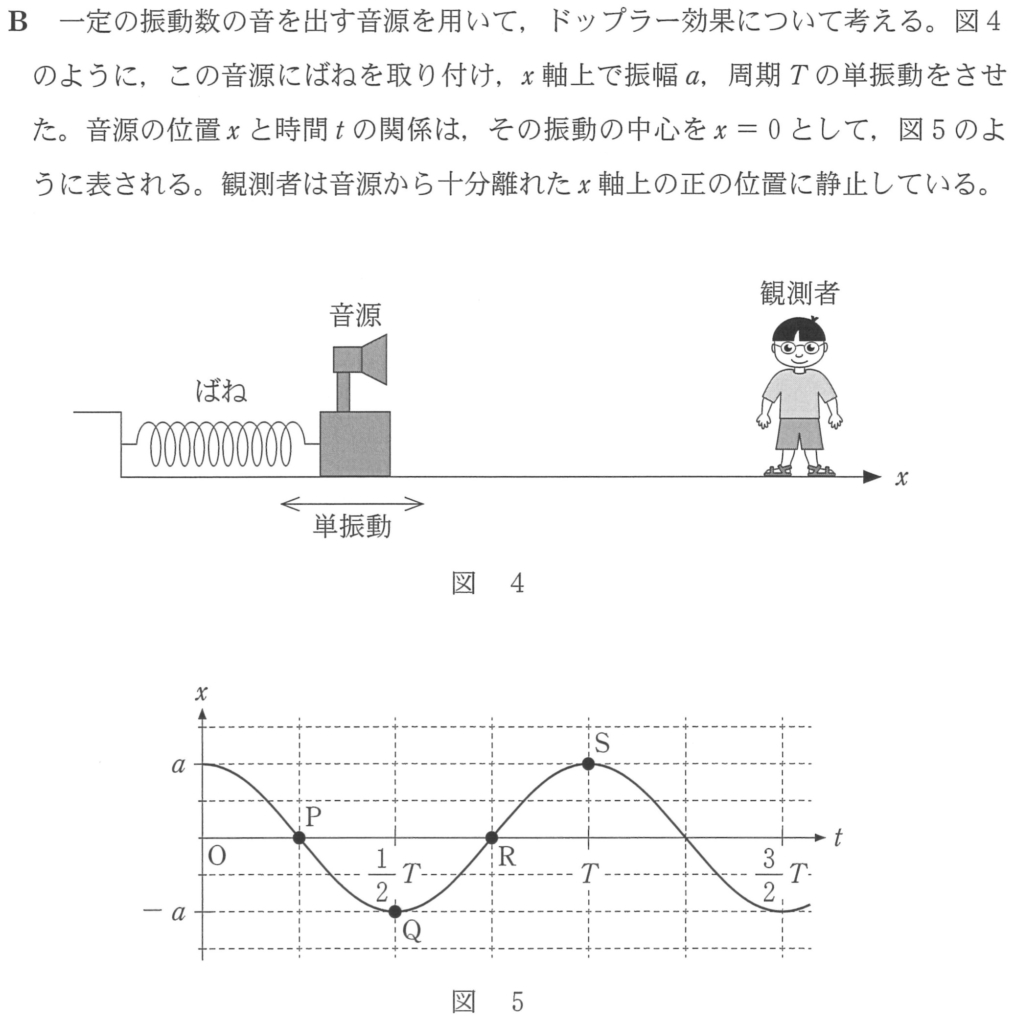
求めたいのは図5のグラフの関係式ね。コサイン(cos)のグラフに見えるけど,選択肢はすべてサイン(sin)の関係式だわ。
物理が得意な秀樹
そうなんだよね。でもまずはコサイン(cos)で表してみようか。縦軸が で,振幅が
で,振幅が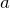 で,角度が
で,角度が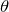 だとすると,どんな式になるかな。
だとすると,どんな式になるかな。
物理が苦手な文子
角度が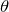 でいいの?だったら,
でいいの?だったら,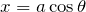 でしょ。でも問題文のどこにも
でしょ。でも問題文のどこにも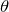 が無いわよ。
が無いわよ。
物理が得意な秀樹
そうだね。グラフの横軸は時刻なので,時刻 と角度
と角度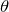 の関係が分かれば答えはでそうだよね。そこで,角振動数
の関係が分かれば答えはでそうだよね。そこで,角振動数 を使うんだ。
を使うんだ。
物理が苦手な文子
さらに新しい文字を使うの?
物理が得意な秀樹
そうなっちゃうね。 は単振動の分野では「角振動数」と呼ぶけど,円運動の分野では「角速度」って呼ぶんだ。どちらも単位は「〔rad/s〕ラジアン毎秒」で,分野によって呼び方が違うだけで物理的には同じなんだ。だから使える公式も同じだよ。確認しておこう。
は単振動の分野では「角振動数」と呼ぶけど,円運動の分野では「角速度」って呼ぶんだ。どちらも単位は「〔rad/s〕ラジアン毎秒」で,分野によって呼び方が違うだけで物理的には同じなんだ。だから使える公式も同じだよ。確認しておこう。


物理が苦手な文子
なるほど。「コサインオメガティー(cos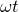 )」という響きは聞いたことがあるわ。
)」という響きは聞いたことがあるわ。
物理が得意な秀樹
そうでしょ。さらに円運動や単振動で使う公式を使って,角振動数 を周期
を周期 を使って表すと,
を使って表すと,
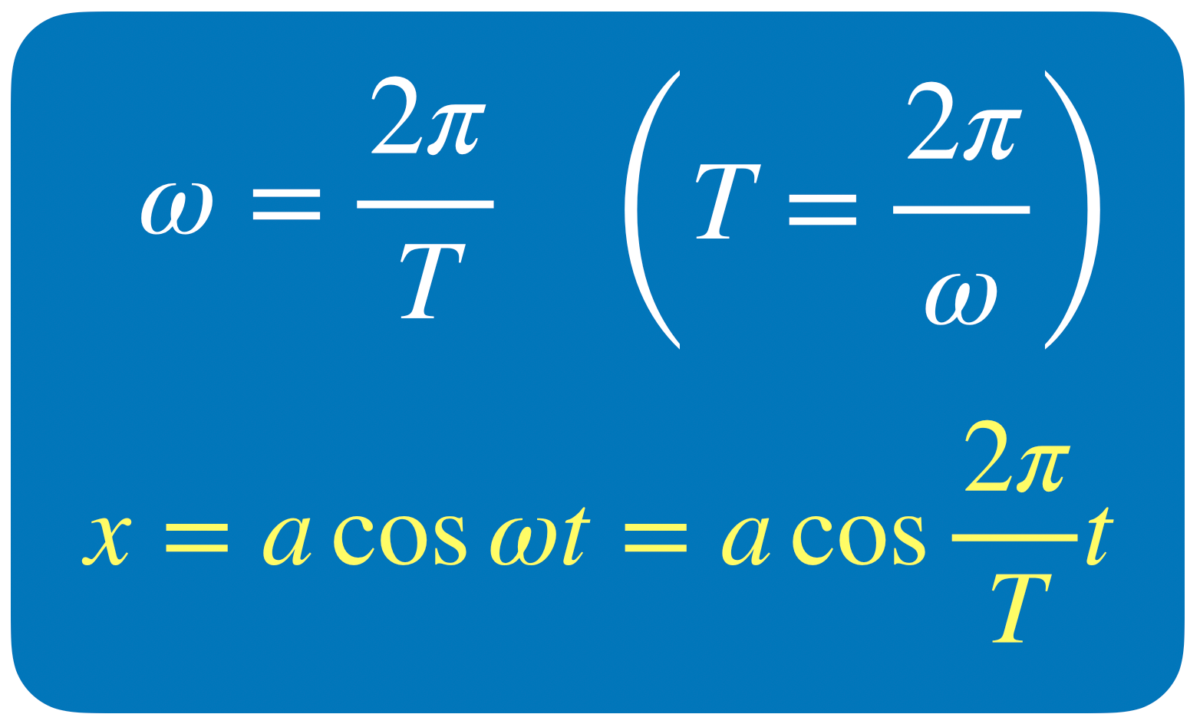
グラフを移動する
物理が苦手な文子
少し選択肢に近づいてきたわね。でも選択肢はサイン(sin)なのよね。
物理が得意な秀樹
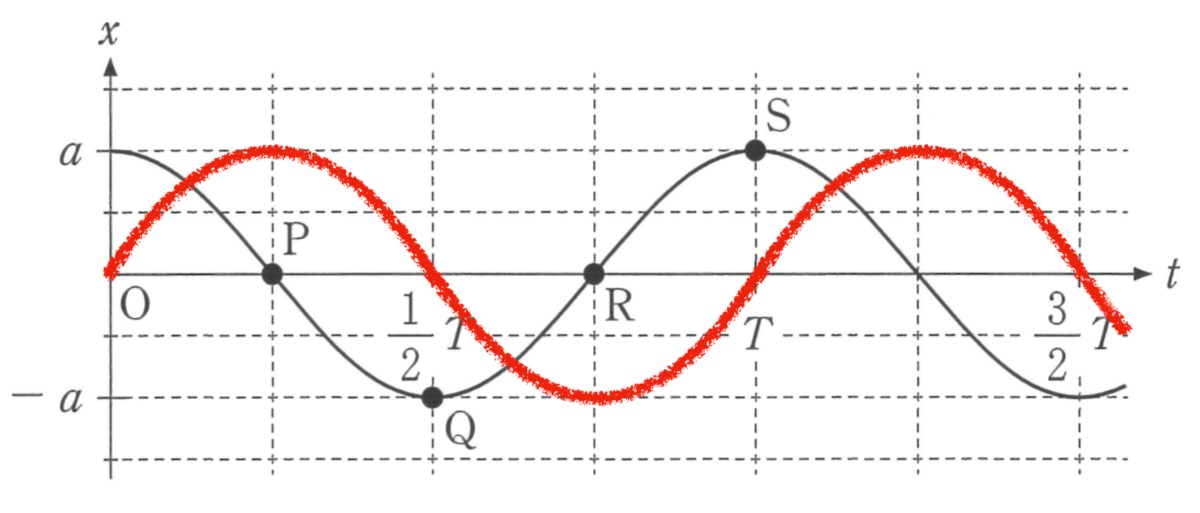
次は問題のグラフとサインのグラフを比較してみよう。この赤いグラフを式で表すとどうなるかな?
物理が苦手な文子
サイン(sin)のグラフだから,こうね。
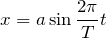
物理が得意な秀樹
そうだね。そのグラフを移動して,コサイン(cos)のグラフにするんだ。
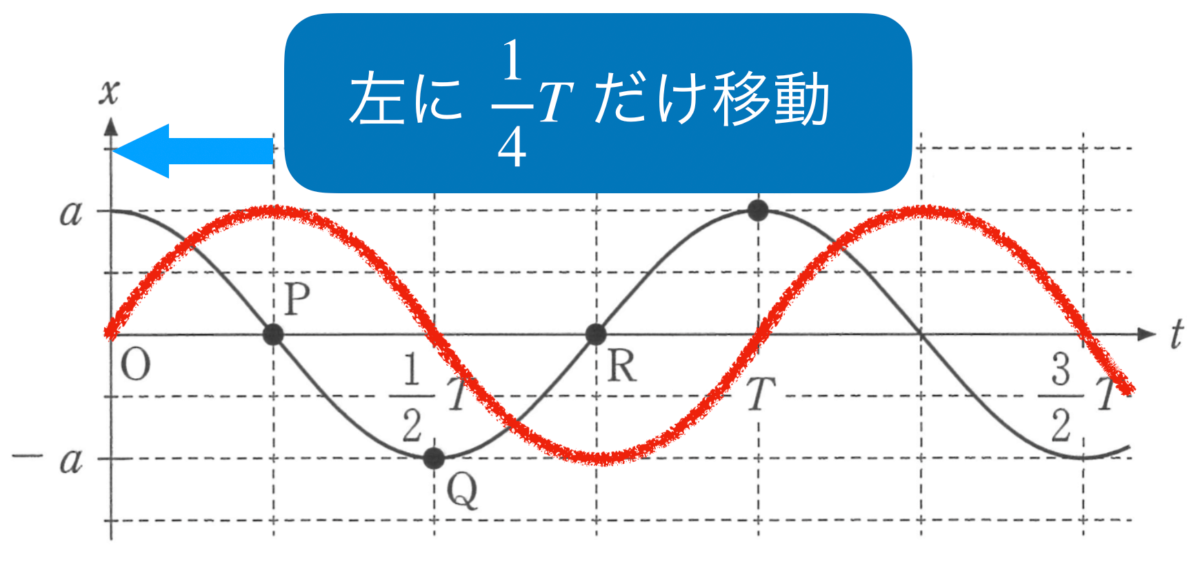
物理が苦手な文子
サイン(sin)のグラフを左に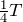 だけ移動するとコサイン(cos)になるわね。
だけ移動するとコサイン(cos)になるわね。
物理が得意な秀樹
ただ,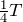 というのは時間だよね。なので,時間を左に動かすのを間違えないでね。
というのは時間だよね。なので,時間を左に動かすのを間違えないでね。
物理が苦手な文子
時間を動かすって,こういうこと?
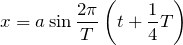
物理が得意な秀樹
そう,あとはカッコの中に入れよう。
物理が苦手な文子
こういうことね。
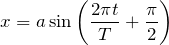
物理が得意な秀樹
そうだね。答えは④だ。
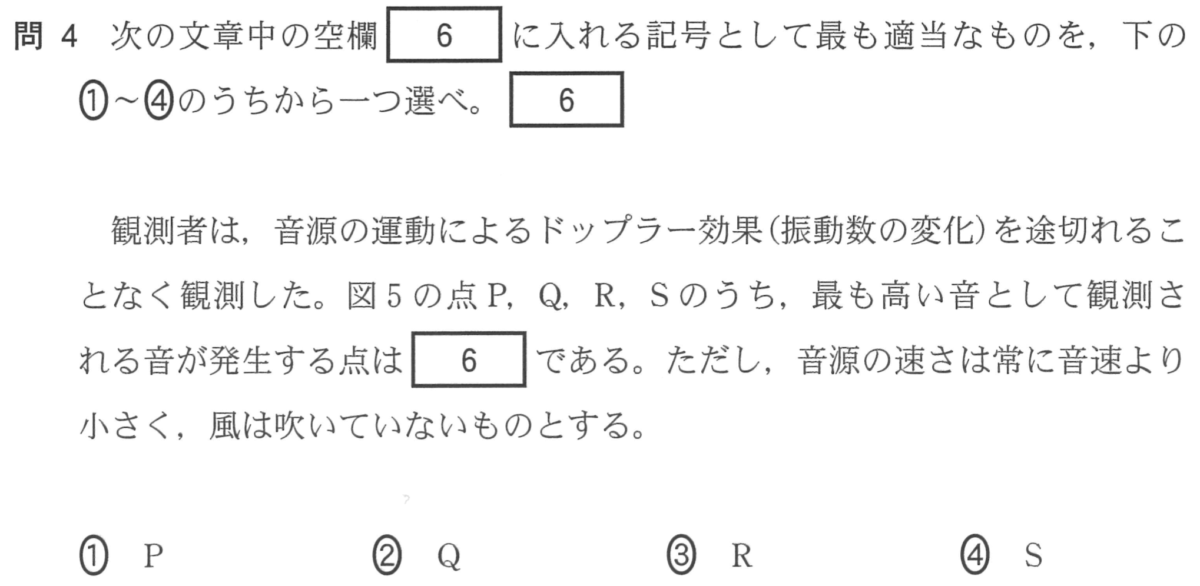
グラフと音源の運動を対応させる
物理が苦手な文子
ドップラー効果では,近づいてくるときに音は高く聞こえるのよね。
物理が得意な秀樹
その通り!なので,グラフと音源の位置関係を確認しておこう。
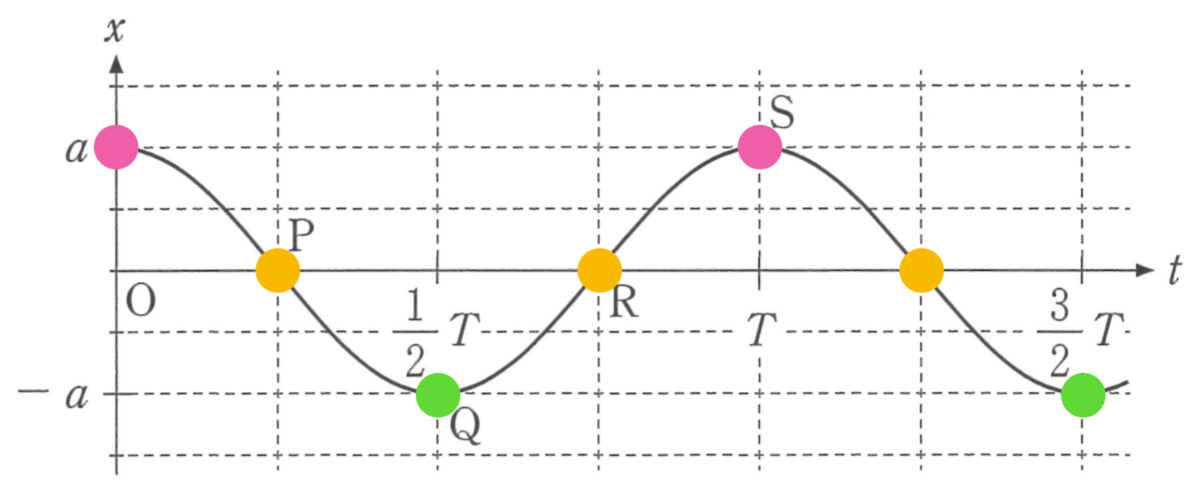
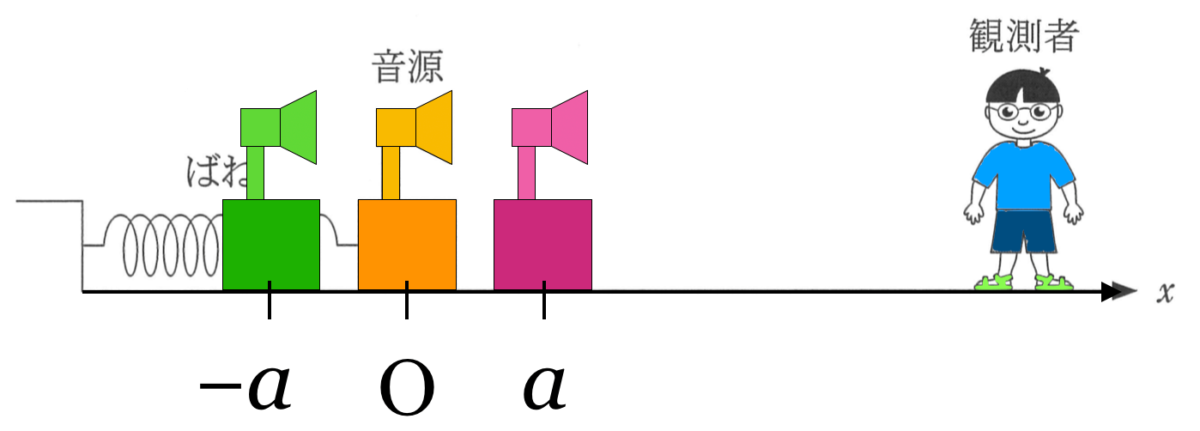
物理が苦手な文子
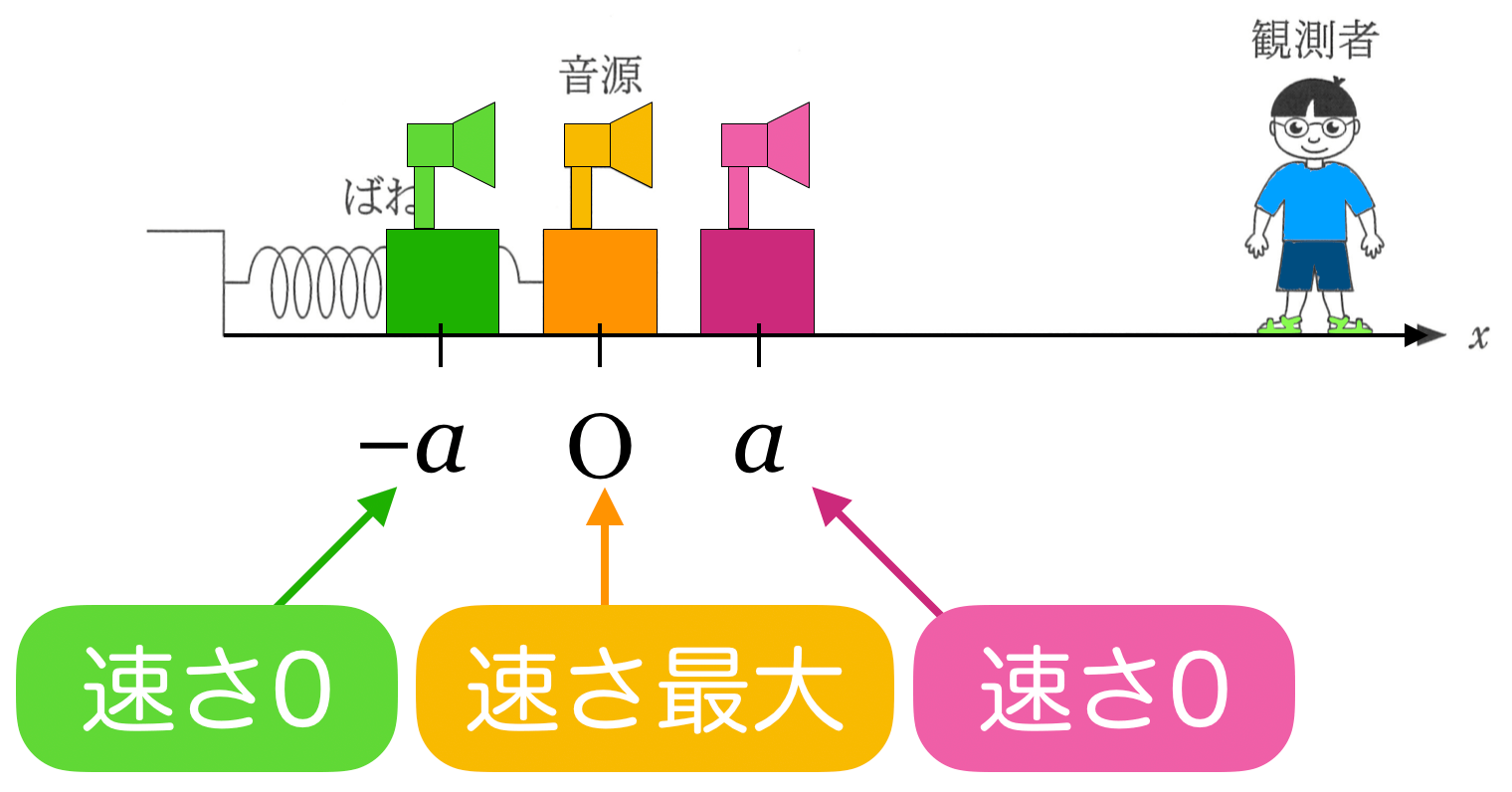
分かりやすくするために色を付けたのね。ということは,一番近いピンク色のSのときが音が高いのね。
物理が得意な秀樹
いやいや違うよ。近づいてくる速さが速いときに出した音が高く聞こえるんだ。
物理が苦手な文子
そうか,単振動での両端は速さが0だったわね。真ん中が一番速いのね。
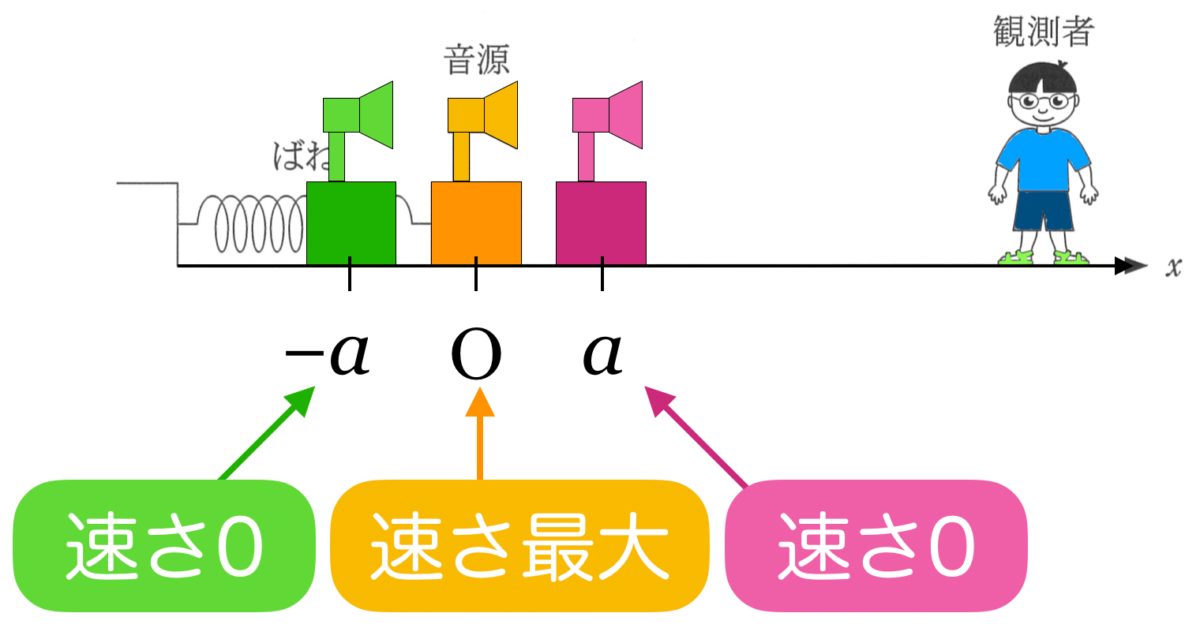
物理が得意な秀樹
その通りだ。速さが最大で,近づいてくるのか遠ざかるのかはグラフで確認しよう。
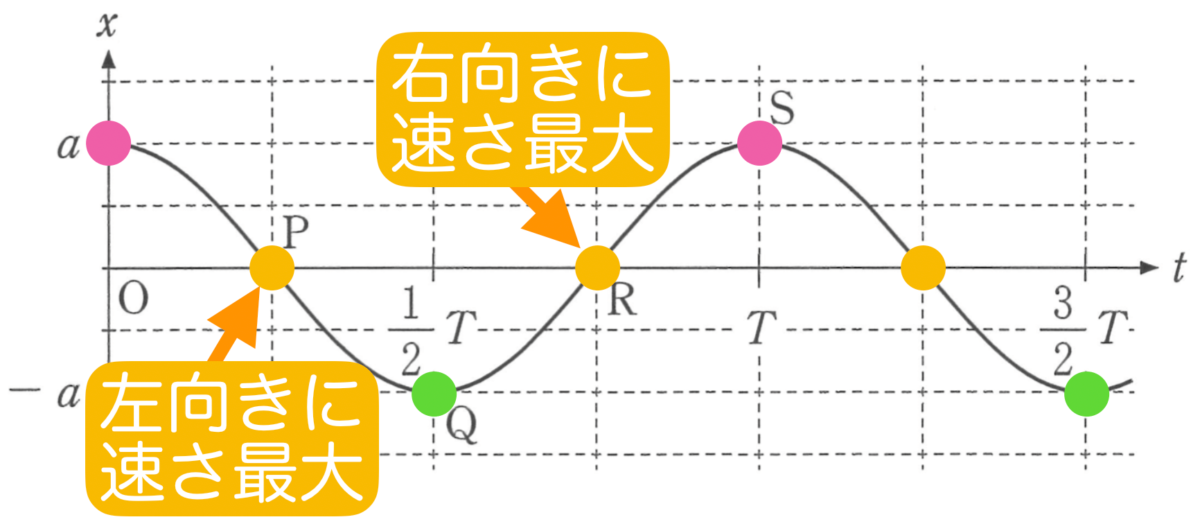
物理が苦手な文子
Pはピンクから緑に動く途中なので左向きで,Rは緑からピンクに動く途中だから右向きということね。近づいているのはRのときね。
物理が得意な秀樹
そういうことだね。答えは③だ。